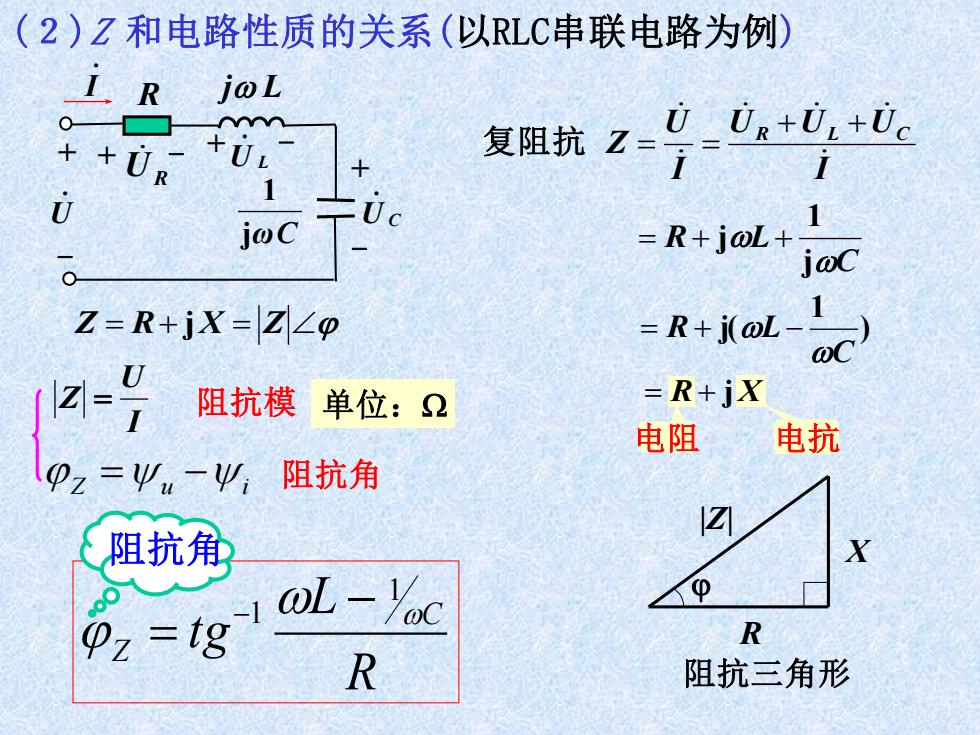
(2)Z和电路性质的关系(以RLC串联电路为例) I.R joL 0 复阻抗Z=7 0R+0.+0c ++UR +UL U jwC 1 =R+j@L+ jwC Z=R+jX=|Z∠p =R+j(@L 阻抗模单位:2 =R+jX 电阻 电抗 p2=-必,阻抗角 ☑ 阻抗角 X ol-Yoc Pz=ig R R 阻抗三角形
电阻 电抗 . I R j L + - + - + - . U U L . U C . jωC 1 + - UR I U U U I U Z R L C + + 复阻抗 = = C R L j 1 = + j + ) 1 j( C R L = + − = R + jX |Z| R X 阻抗三角形 Z = u − i 单位: I U Z = 阻抗模 阻抗角 Z = R+ jX = Z (2)Z 和电路性质的关系(以RLC串联电路为例) R L t g C Z 1 1 − = − 阻抗角
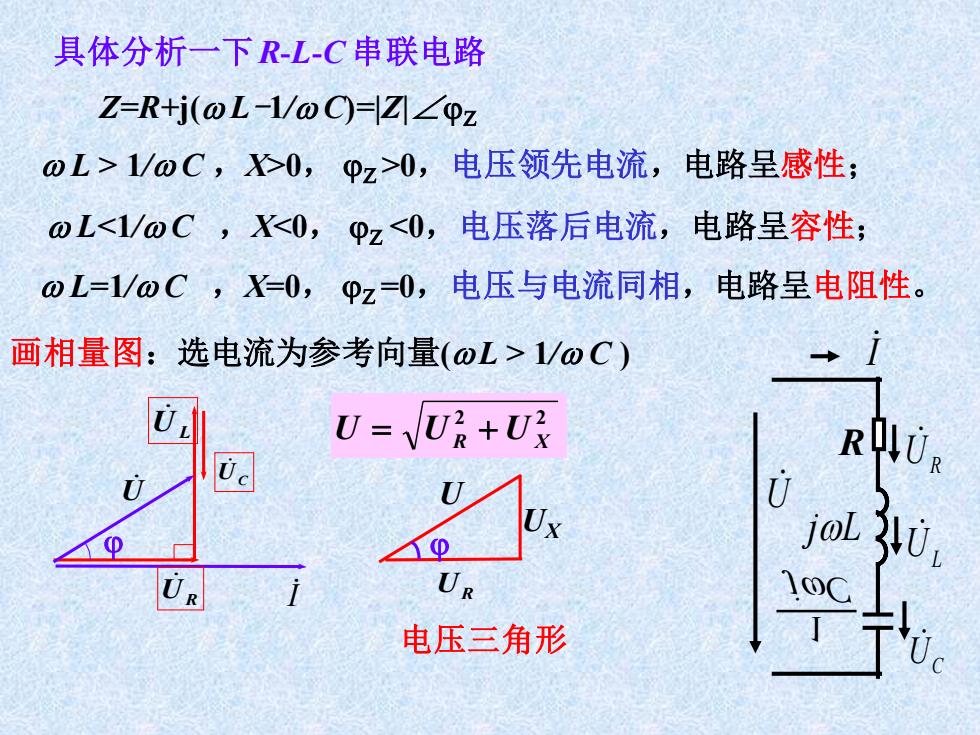
具体分析一下R-L-C串联电路 Z=R+j(oL-1/oC-Z☑∠0z oL>1/oC,0,pz>0,电压领先电流,电路呈感性: oL<1/oC,X<0, φ2<0,电压落后电流,电路呈容性; oL=1/@C,X=0,p2=0,电压与电流同相,电路呈电阻性。 画相量图:选电流为参考向量(oL>1/oC) U-JUR+Ux RUR joL UR 电压三角形
具体分析一下R-L-C 串联电路 Z=R+j( L-1/ C)=|Z|∠Z L > 1/ C ,X>0, Z >0,电压领先电流,电路呈感性; L<1/ C ,X<0, Z <0,电压落后电流,电路呈容性; 画相量图:选电流为参考向量( L > 1/ C ) UC I UR UL U 2 2 U = UR + U X 电压三角形 UX UR U L=1/ C ,X=0, Z =0,电压与电流同相,电路呈电阻性。 R UR UL UC I U jL jC 1

ROUR 假设R、L、C已定, 电路性质能否确定? joL 0 (阻性?感性?容性? 不能! XL=0L、XC= @C 当w不同时,可能出现: X>Xc,或X<Xc,或X-Xc。 2-81
假设R、L、C已定, 电路性质能否确定? (阻性?感性?容性?) 不能! 当ω不同时,可能出现: XL > XC ,或 XL < XC , 或 XL =XC 。 C XL L XC 1 = 、 = 2-81 R UR UL UC I U jL jC 1
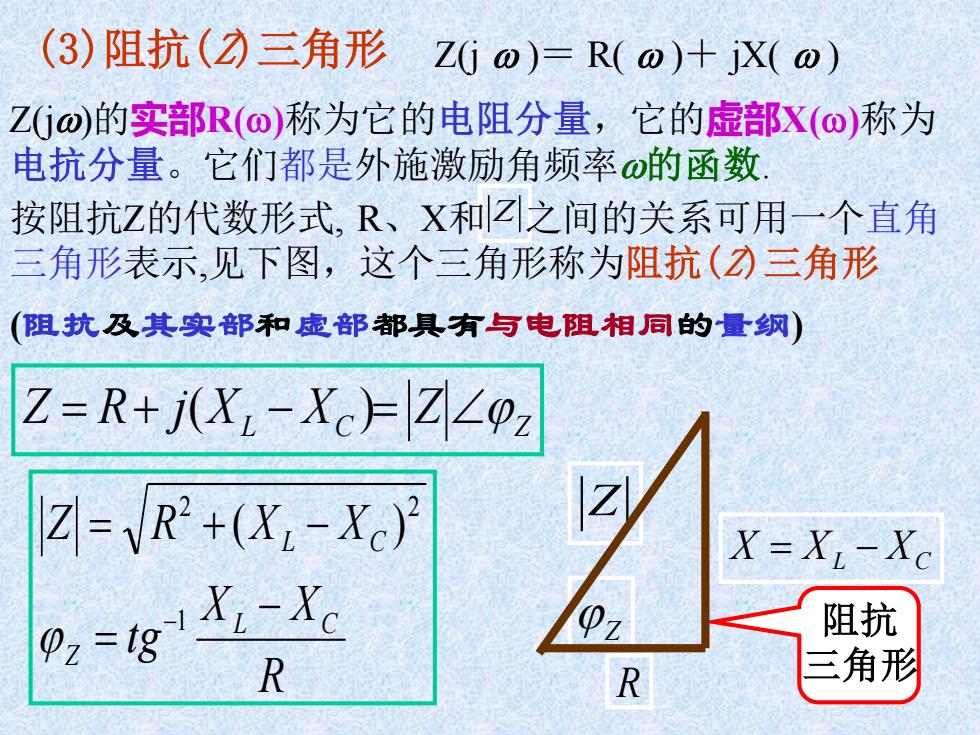
(3)阻抗()三角形 Z(Gw)=R(0)+jX(0) Z(jo)的实部R(@)称为它的电阻分量,它的虚部X(O)称为 电抗分量。它们都是外施激励角频率⊙的函数 按阻抗Z的代数形式,R、X和Z之间的关系可用一个直角 三角形表示,见下图,这个三角形称为阻抗()三角形 (阻抗及其实部和虚部都具有与电阻相同的量纲) Z=R+jX-Xc上|Z∠pz Z=R2+(X-Xc) X=XI-XC 0,=g- 阻抗 R R 三角形
(3)阻抗(Z)三角形 阻抗 三角形 Z Z R X = XL − XC R X X t g Z R X X L C Z L C − = = + − −1 2 2 ( ) XL XC Z Z Z = R+ j( − )= Z(j )= R( )+ jX( ) Z(j)的实部R()称为它的电阻分量,它的虚部X()称为 电抗分量。它们都是外施激励角频率的函数. 按阻抗Z的代数形式, R、X和 Z 之间的关系可用一个直角 三角形表示,见下图,这个三角形称为阻抗(Z)三角形 (阻抗及其实部和虚部都具有与电阻相同的量纲)
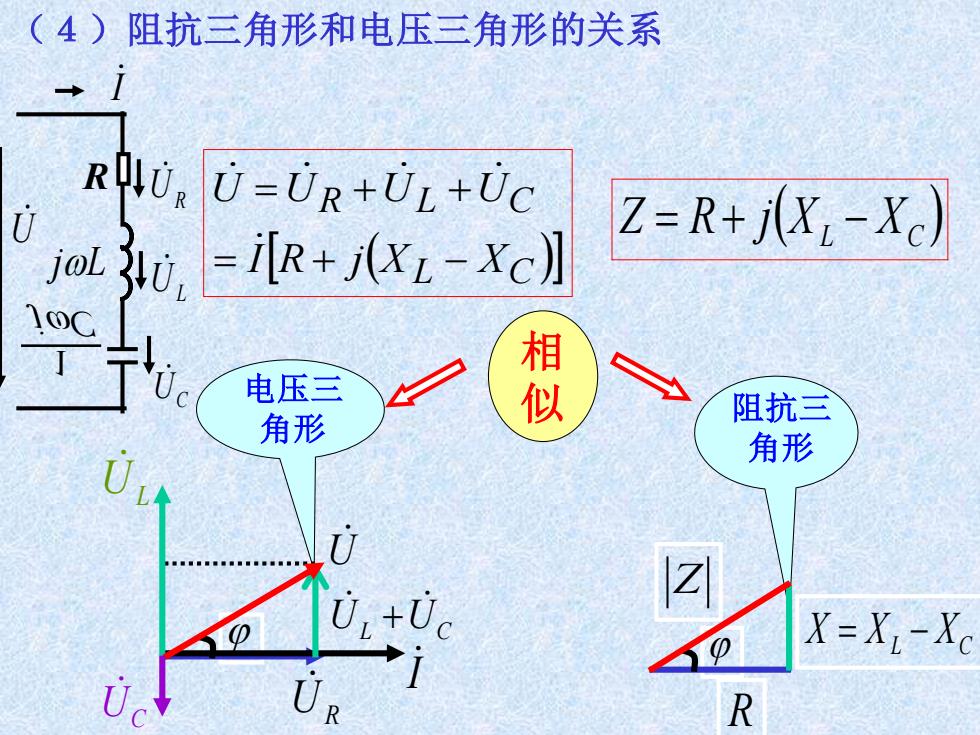
(4)阻抗三角形和电压三角形的关系 ROLU U=UR+UL+UC Z=R+j(Xi-Xc) =[R+XL-Xc〗 电压三 似 角形 阻抗三 角形 X=XL-Xc R
(4)阻抗三角形和电压三角形的关系 电压三 角形 阻抗三 角形 相 似 ( C ) L R L C I R j X X U U U U = + − = + + ( ) XL XC Z = R + j − Z R X XL XC = − UC UR U UL UL UC + I R UR UL UC I U jL jC 1