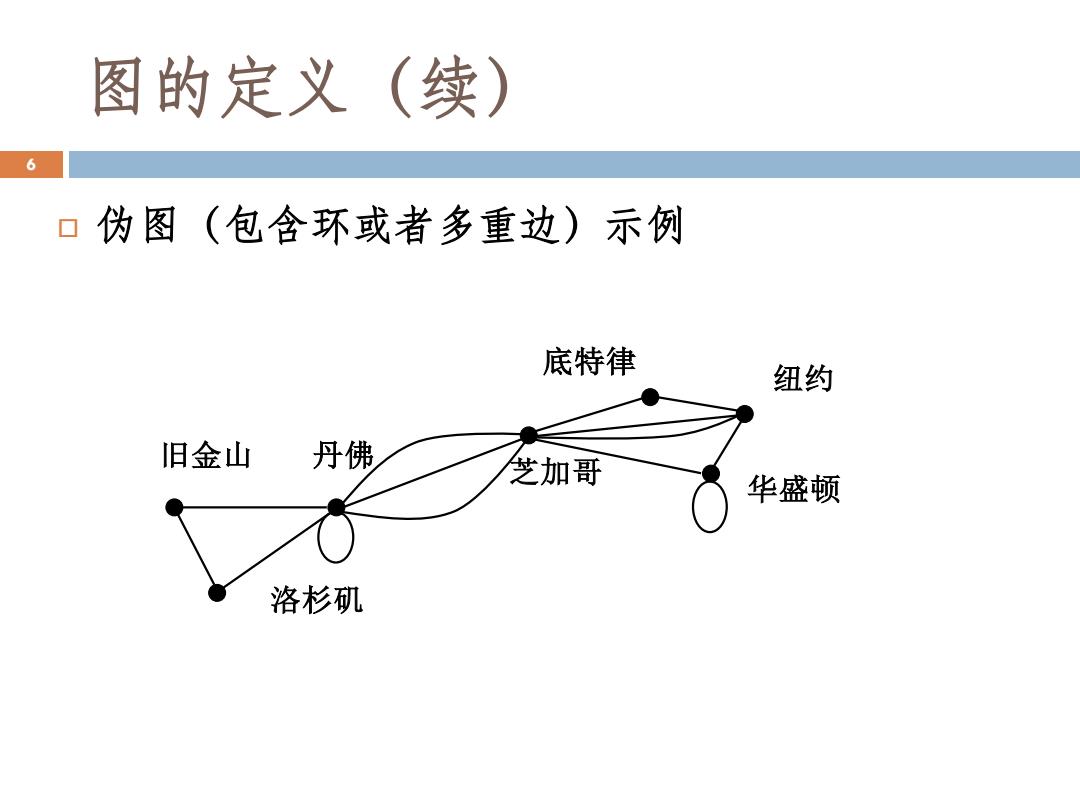
图的定义(续) 6 口伪图(包含环或者多重边)示例 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶
图的定义(续) 伪图(包含环或者多重边)示例 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 6
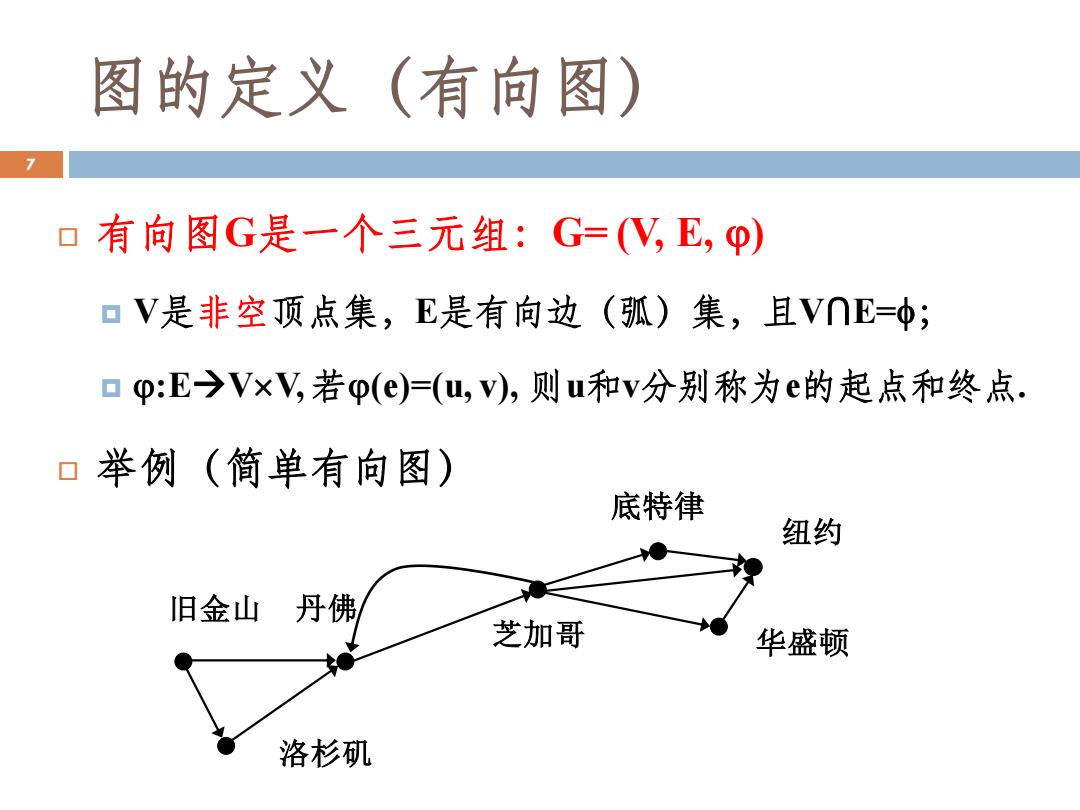
图的定义(有向图) 7 口有向图G是一个三元组:G=(V,E,φ) 口V是非空顶点集,E是有向边(弧)集,且V∩E=中; 口p:E→V×V,若p(e)=(u,v),则u和v分别称为e的起点和终点. 举例(简单有向图) 底特律 纽约 旧金山丹佛 芝加哥 华盛顿 洛杉矶
图的定义(有向图) 有向图G是一个三元组:G= (V, E, ) V是非空顶点集,E是有向边(弧)集,且V⋂E=; :E→VV,若(e)=(u, v), 则u和v分别称为e的起点和终点. 举例(简单有向图) 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 7

图的术语 8 口无向图G=(V,E,p),φ(e)={u,} ▣u和v在G里邻接(相邻) ▣e关联(连接)顶点u和v 图G中顶点v的度,deg(v),dc() 口与该顶点关联的边数,环为顶点的度做出双倍贡献。 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶
无向图G = (V, E, ), (e)={u, v} u和v在G里邻接(相邻) e关联(连接)顶点u和v 图G中顶点v的度, deg(v), dG (v) 与该顶点关联的边数,环为顶点的度做出双倍贡献。 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 8 图的术语

握手定理 9 ▣无向图G有m条边,n个顶点V1,Vn ∑dy,)=2m 1 ▣推论:无向图中奇数度顶点必是偶数个
无向图G有m条边,n个顶点v1 , …vn . 推论:无向图中奇数度顶点必是偶数个。 d v m n i i ( ) 2 1 = = 9 握手定理

图的术语(续) 10 ▣有向图G=(V,E,p),p(e)=(u,v) 口u是e的起点,v是e的终点 口假设u≠V,u邻接到v,v从u邻接 口有向图中顶点的出度和入度 口dg+(v)=以v为始点的边的条数,degt(v) 口dg(v)=以v为终点的边的条数,deg(v) 口有向图中各顶点的出度之和等于入度之和。 Σveydeg((v)=∑vey deg()=El 口有向图的底图
有向图G =(V, E, ), (e)=(u, v) u是e的起点,v是e的终点 假设 uv,u邻接到v,v从u邻接 有向图中顶点的出度和入度 dG + (v) = 以v为始点的边的条数,deg+ (v) dG - (v) = 以v为终点的边的条数,deg- (v) 有向图中各顶点的出度之和等于入度之和。 vVdeg+ (v) = vV deg- (v) =|E| 有向图的底图 10 图的术语(续)