
西安毛子科技大学映射XIDIAN UNIVERSITY说明:映射又称为算子.在不同数学分支中有不同的惯用名称.例如,f:X→YX为非空集合,Y为数集,f称为X上的泛函X为实数集合(或其子集),Y为数集,f称为X上的函数X为非空集合,Y为其子集,f称为X上的变换
映射 说明: 映射又称为算子.在不同数学分支中有不同的惯用名称.例如, 为非空集合, 为数集, 称为 上的泛函 为实数集合(或其子集), 为数集, 称为 上的函数 为非空集合, 为其子集, 称为 上的变换

西安毛子科技大学映射XIDIANUNIVERSITY逆映射:若映射 f:X→Y 为单射,即VyEf(X),存在唯一xX,有f(x)=y, 定义f(X)-→Xg:.y→x称g为f的逆映射习惯上,=f(x),xEX的逆映射记成 =-(x),xEf(X)即 D,-(x)= Rr(a),Dr(x) = Rf -(c)
映射 逆映射: 若映射 为单射,即 存在唯一 有 定义 称 为 的逆映射 习惯上, y f x x X = ( ), 的逆映射记成 1 y f x x f X ( ), ( ) − = 即 1 ( ) ( ) , − = f x f x D R 1 ( ) ( ) = − f x f x D R

西安毛子科技大学映射XIDIAN UNIVERSITY复合映射:g手电筒复合映射DD2
映射 复合映射: D1 手电筒 D D D2 复合映射
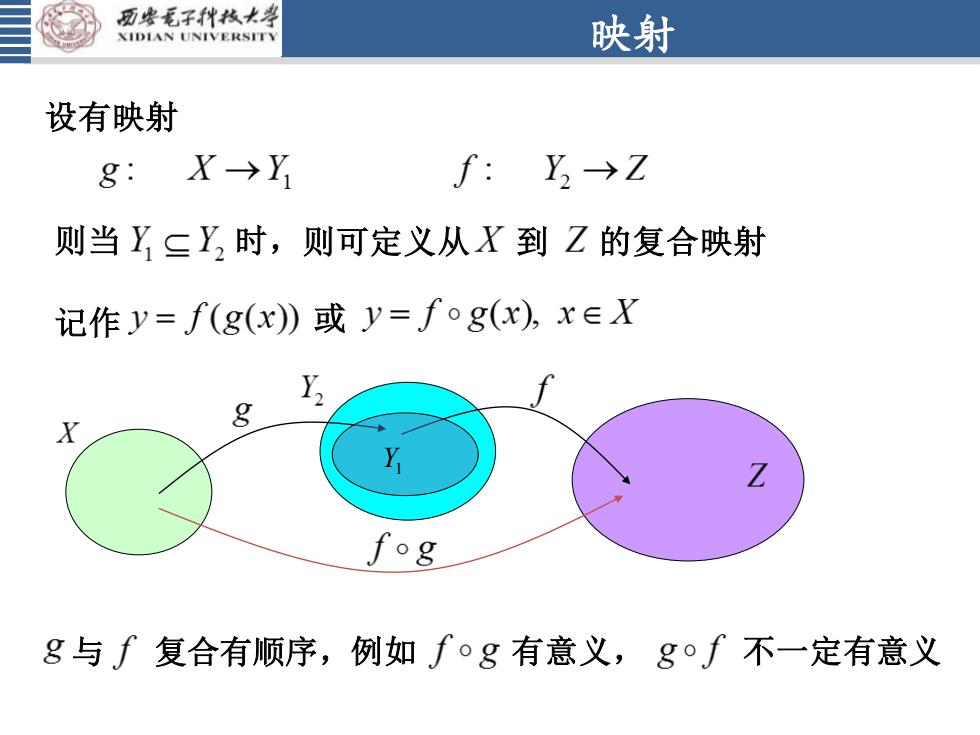
西安毛子科技大学映射XIDIANUNIVERSITY设有映射X→YY→Zf :g:则当YCY时,则可定义从X到Z的复合映射记作y= f(g(x) 或 y=f og(x), xEXY,gXYfogg与f复合有顺序,例如fog有意义,gof不一定有意义
映射 设有映射 则当 时,则可定义从 到 的复合映射 记作 或 Y1 与 复合有顺序,例如 有意义, 不一定有意义