
西安毛子科技大学数学与统计学院School of mathematies and statistiesXIDIAN UNIVERSITY西等数学第九节闲区间上连续函数的性质
第九节 闭区间上连续函数的性质

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY一、最大最小值定理1.定义f(x)是定义在区间I上的函数,如果 日x。EI,使得对于xI,都有f(x)≤f(x) (f(x)≥f(x)则称f(x)是函数在区间I上的最大值(最小值)
闭区间上连续函数的性质 1. 定义 一、最大最小值定理 对于 都有 (最小值). 是定义在区间 上的函数,如果 使得 则称 是函数在区间 上的最大值
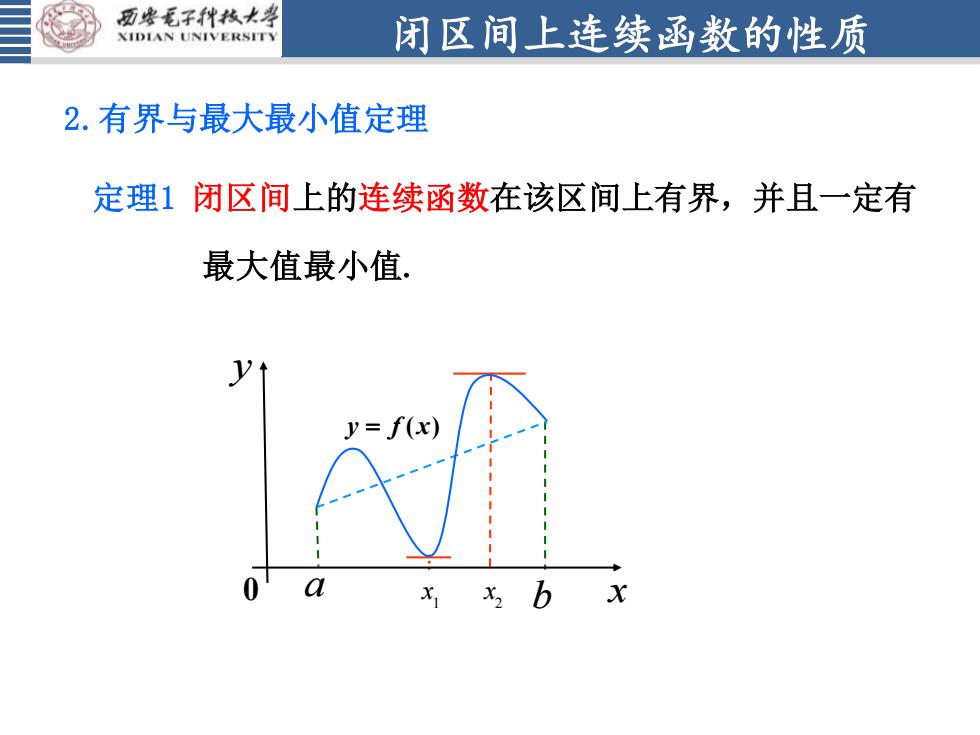
西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY2.有界与最大最小值定理定理1闭区间上的连续函数在该区间上有界,并且一定有最大值最小值山f(x)0abxxX2
闭区间上连续函数的性质 定理1 闭区间上的连续函数在该区间上有界,并且一定有 2.有界与最大最小值定理 最大值最小值. 1 x 2 x y = f (x) a 0 b x y

西安毛子科技大学闭区间上连续函数的性质XIDIANUNIVERSIT注若定理条件不满足,即函数在开区间上连续,或在闭区间内有间断点,定理的结论不一定成立2例如y=x,xE(O,1)无最大值和最小值在[0,2]上也[-x+1, 0≤x<1例如1, x=1f(x)=无最大值和-x+3, 1<x≤2最小值.元元例如 =tanx在开区间(-连续,但没有界22[1x+0例如V=x在闭区间[-1,1] 不连续,无界0x=0
闭区间上连续函数的性质 无最大值和最小值. o x y 1 1 x o y 1 1 2 2 在[0,2]上也 无最大值和 最小值. 注 若定理条件不满足,即函数在开区间上连续,或在闭区 间内有间断点,定理的结论不一定成立. 例如 在开区间 连续,但没有界. 例如 例如 例如 在闭区间 不连续,无界

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY三、零点定理1.定义如果存在x使得f(α)=0,则x称为函数f(α)的零点x。为函数 f(x)的零点<> x。为方程f(x)=0的根>曲线y=f(x)与x轴有交点
闭区间上连续函数的性质 三、零点定理 如果存在 使得 ,则 称为函数 的零点. 1. 定义 为函数 的零点 为方程 的根. 曲线 y f x x = ( ) 与 轴有交点