注意 证明切比雪夫大数定律主要的数学工 具是切比雪夫不等式. 设随机变量X有期望E(X)=4,方差 D(X)=σ2,则对于任意的e>0, P1X-E(XKe≥1-o 或PIX-EX)esO 切比雪夫不等式
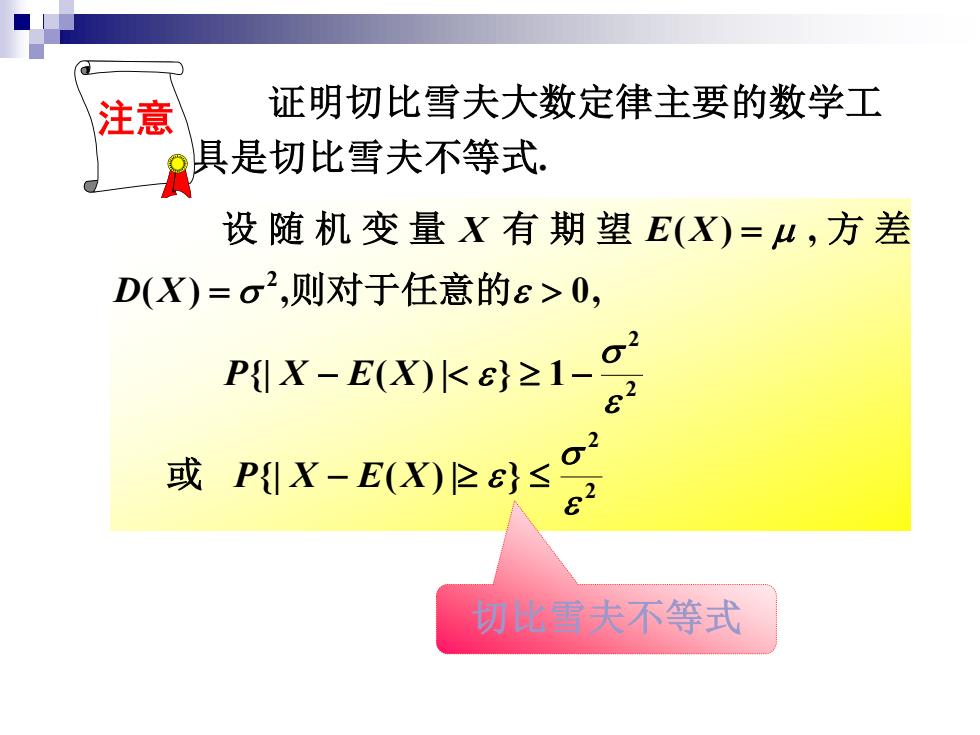
证明切比雪夫大数定律主要的数学工 具是切比雪夫不等式. 注意 设 随 机 变 量 X 有期望 E(X) = , 方 差 2 D(X) = ,则对于任意的 0, 2 2 {| ( )| } 1 P X − E X − 或 2 2 {| ( )| } P X − E X 切比雪夫不等式

说明 不等式给出了在随机变量X的分布未知的 情况下,事件X-4<}概率的一种估计方法。 例 ε=3o,P{X-uK}=P{X-K3σ≥0.8889 8=4oP{X-K}=P{X-K4σ}≥0.9375
说明 例 =3 , P {|X- |< }= P {|X- |< 3 }0.8889 =4 P {|X- |< }=P {|X- |< 4 }0.9375 不等式给出了在随机变量 X 的分布未知的 情况下,事件{| X − | }概率的一种估计方法

例掷一颗骰子1620次,估计“六点”出现的次数 X在250~290之间的概率? 解X~b1620, E(X)=p=1620×=270 6 D(X)=p(1-p)=1620×x5=225 66 由切比雪夫(Chebyshev)不等式估计 P{250<X<290}=P{X-270k20} 225 ≥1- 202 =0.4375
例 掷一颗骰子1620次,估计“六点”出现的次数 X在250~290之间的概率? 解 由切比雪夫(Chebyshev)不等式估计 ) 6 1 X ~ b(1620, E(X) = 270 6 1 np = 1620 = D(X) = 225 6 5 6 1 np(1 − p) = 1620 = P{250 X 290} = P{| X − 270 | 20} 2 20 225 1 − = 0.4375

切比雪夫(Chebyshev)定理证明 设随机变量X1,X2,Xn相互独立,且具有相同 的数学期望和方差,E(Xk)=4,D(Xk)=o2, =12,做前个随机变量的算术平均,=之X。 则对于任意正数ε,有 lim P{Y -uK<& =imPI2X-水=1 k-1
设随机变量 X1 ,X2 ,., Xn 相互独立,且具有相同 的 数 学 期 望 和 方 差 , E(Xk ) = , 2 D(Xk ) = , (k = 1,2, ),做前n个随机变量的算术平均 = = n k n Xk n Y 1 1 , 则对于任意正数 ,有 | } 1 1 lim {| lim {| | } 1 = − = − = → → n k k n n n X n P P Y 切比雪夫(Chebyshev)定理证明

E2X1=之EX)=u=4 k=1 m名x1-2x)-开 :P1∑x-4ke≥1-n 2 k- 令n→oo,且概率不能大于H,有 i-4k=mPI2x-4水e=l n k=1
= = ] 1 [ 1 n k Xk n E = = n k E Xk n 1 ( ) 1 n = n 1 = = ( ) 1 1 2 n k D Xk = n = ] 1 [ 1 n k Xk n D = 2 2 1 n n n 2 | } 1 {| 1 − = n k Xk n P 2 2 1 n − − = → lim {| | } n n P Y 令n → ,且概率不能大于1,有 | } 1 lim {| 1 − = → n k k n X n P = 1