导航 学以致用 1,如图,在直三棱柱ABC-A1BC1中,AC=3,BC=4,AB=5,AA1=4, 求证:AC⊥BC B A1 B
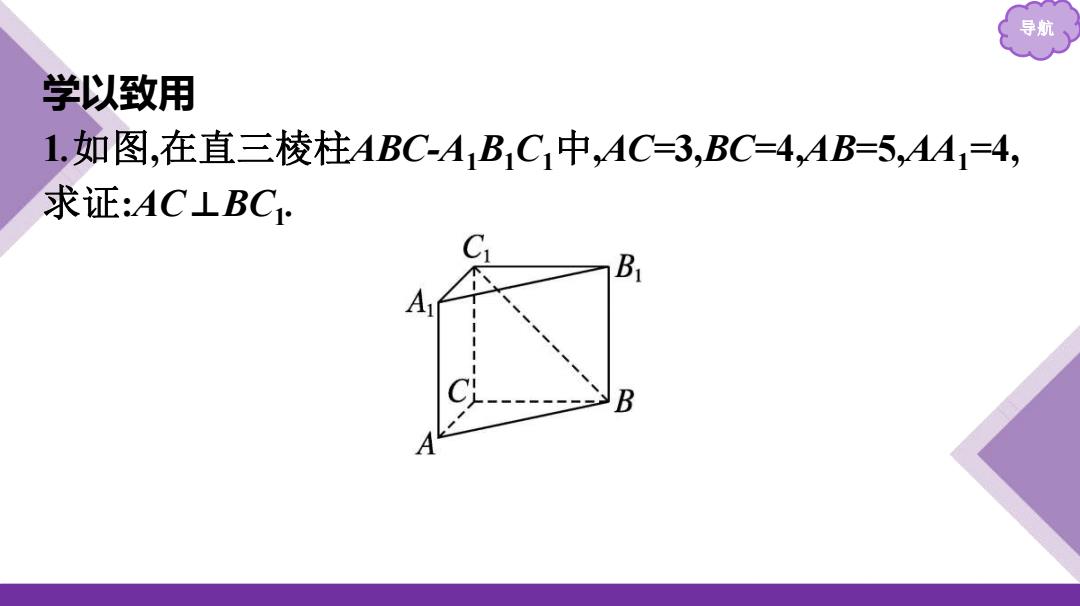
导航 学以致用 1.如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1 =4, 求证:AC⊥BC1

导 证明:.AC=3,BC=4,AB=5,∴AC⊥BC 又在直三棱柱ABC-A1BC1中,CC1⊥平面ABC, AC,BC,C1C两两互相垂直 如图,以C为原点,CA,CB,CC所在直线分别为x轴、y轴、轴, 建立空间直角坐标系. 则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0), B A AC=(-3,0,0),BC1=(0,-4,4), ∴.AC.BC=0. B .AC⊥BC1
导航 证明:∵AC=3,BC=4,AB=5,∴AC⊥BC. 又在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC, ∴AC,BC,C1C两两互相垂直. 如图,以C为原点,CA,CB,CC1所在直线分别为x轴、y轴、z轴, 建立空间直角坐标系. 则C(0,0,0),A(3,0,0),C1 (0,0,4),B(0,4,0), ∵𝑨 𝑪 =(-3,0,0),𝑩𝑪𝟏 =(0,-4,4), ∴𝑨 𝑪 ·𝑩𝑪𝟏 =0. ∴AC⊥BC1