
微训练若平面a1平面A平面a的个法向量为m-((21,2)则 平面的法向量m可以为(C) A(1,2) B.(2,-1,0) C.(1,2,0) D(61,2) 解析:.平面aL平面B,∴n=0. 将选项代入验证,可知C满足.故选C
导航 微训练若平面α⊥平面β,平面α的一个法向量为n= ,则 平面β的法向量m可以为( ) -2,1, 1 2 A. -1, 1 2 , 1 4 B.(2,-1,0) C.(1,2,0) D. 1 2 ,1,2 C 解析:∵平面α⊥平面β,∴n·m=0. 将选项代入验证,可知C满足.故选C
导航 课堂·重难突破 证明线线垂直 典例剖析 A 1.已知正三棱柱ABC-A B C,的各棱长都为 C 1,M是BC的中点,N是CC上的点,且 B CN=CC1,求证:AB1⊥MN
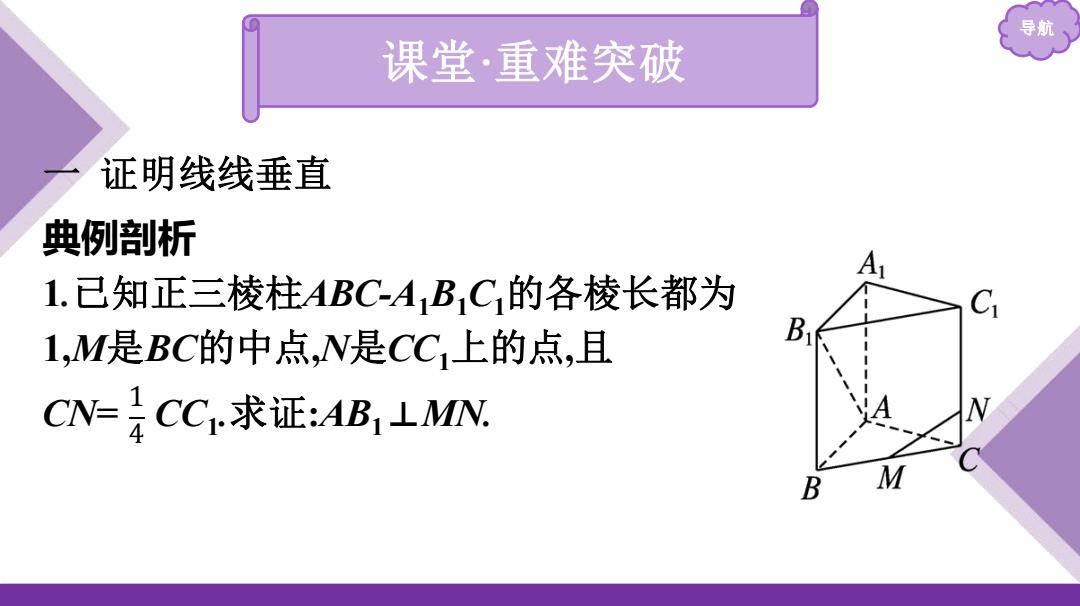
导航 课堂·重难突破 一 证明线线垂直 典例剖析 1.已知正三棱柱ABC-A1B1C1的各棱长都为 1,M是BC的中点,N是CC1上的点,且 CN= CC1 .求证:AB1⊥MN. 1 4

导航 证明:如图,以AB的中点O为原点,建立空间直角坐标系. 由已知得1(20,0),M(0),N(0,),B1(20,1, 所以MN-(是),AB-(1,01, B 所以MN.AB1-+0+}0. 所以MN⊥AB,所以AB1⊥MN
导航 证明:如图,以AB的中点O为原点,建立空间直角坐标系. 由已知得,A - 𝟏 𝟐 ,0,0 ,M 𝟏 𝟒 , 𝟑 𝟒 ,0 ,N 0, 𝟑 𝟐 , 𝟏 𝟒 ,B1 𝟏 𝟐 ,0,1 , 所以𝑴 𝑵 = - 𝟏 𝟒 , 𝟑 𝟒 , 𝟏 𝟒 ,𝑨𝑩𝟏 =(1,0,1), 所以𝑴 𝑵 ·𝑨𝑩𝟏 =- 𝟏 𝟒 +0+ 𝟏 𝟒 =0. 所以𝑴 𝑵 ⊥ 𝑨𝑩𝟏 ,所以 AB1⊥MN

规律总结利用空间向量证明两条直线垂直的常用方法及步 骤: ()基向量法 ①选取三个不共面的已知向量(通常是它们的模及其两两夹 角为已知)为空间的一个基底; ②把两条直线的方向向量用基底表示; ③利用向量的数量积运算,计算出两条直线的方向向量的数 量积为0,得到方向向量垂直; ④由方向向量垂直得到两条直线垂直
导航 规律总结 利用空间向量证明两条直线垂直的常用方法及步 骤: (1)基向量法 ①选取三个不共面的已知向量(通常是它们的模及其两两夹 角为已知)为空间的一个基底; ②把两条直线的方向向量用基底表示; ③利用向量的数量积运算,计算出两条直线的方向向量的数 量积为0,得到方向向量垂直; ④由方向向量垂直得到两条直线垂直

导期 2)坐标法 ①根据已知条件和图形特征,建立适当的空间直角坐标系,正 确地写出各点的坐标; ②根据所求出的点的坐标求出两条直线的方向向量的坐标; ③计算出两条直线的方向向量的数量积为0,得到方向向量垂 直; ④由方向向量垂直得到两条直线垂直
导航 (2)坐标法 ①根据已知条件和图形特征,建立适当的空间直角坐标系,正 确地写出各点的坐标; ②根据所求出的点的坐标求出两条直线的方向向量的坐标; ③计算出两条直线的方向向量的数量积为0,得到方向向量垂 直; ④由方向向量垂直得到两条直线垂直