
带无纹波,过渡带平缓,群延迟较好。 >切比雪夫函数(Chebyshev):全极点系统,极点均匀的分布在单位圆内的椭 圆上,极点的Q值比巴特沃斯高,通带有纹波,过渡带比较狭窄,群延迟 比巴特沃斯函数差。 >反切比雪夫函数(Chebyshev I):存在n个极点,n-1个零点,极点位于单 位圆的内外侧,零点分布在虚轴上,阻带有纹波。 >椭圆函数(Elliptic):存在n个极点,n-1个零点,极点位于单位圆的内外侧, 零点分布在虚轴上,通带、阻带均有纹波。相比于巴特沃斯和切比雪夫函数, 椭圆函数具有更狭窄的过渡带,但是群延迟也更差。 2.3滤波器的综合 滤波器的综合方式很多,比如:基于RC的综合、基于LC的综合以及基于 Biquad的综合。基于RC的综合只能够实现实数极点,而基于LC的综合不适 用于集成芯片中,在这里便不作详细的叙述。本文中所涉及的综合方式,都是 基于Biquad结构,其中最常用的是Tow-Thomas和Sallen-Key结构。从电路 结构上来说,Sallen-Key结构和Tow-Thomas结构的区别在于,Sallen-Key结 构使用一个运放实现两个极点,而Tow-Thomas结构使用两个运放实现两个极 点。 对于Sallen-Key结构,有以下表达式成立[13: w6= (2.13) √JRRC,C2 Q=( RC2 C+c) (2.14) 假设R1=R2=R,得到: w6= (2.15) RC.C2 0-+8 (2.16) 如果单从功耗上进行考量,Sallen-Key结构显然更具有优势。但是,由于 Sallen-Key结构随工艺和温度变化较为敏感,而且在高频时易受寄生电容的影 13
13 带无纹波,过渡带平缓,群延迟较好。 ¾ 切比雪夫函数(Chebyshev I):全极点系统,极点均匀的分布在单位圆内的椭 圆上,极点的 Q 值比巴特沃斯高,通带有纹波,过渡带比较狭窄,群延迟 比巴特沃斯函数差。 ¾ 反切比雪夫函数(Chebyshev II):存在 n 个极点,n–1 个零点,极点位于单 位圆的内外侧,零点分布在虚轴上,阻带有纹波。 ¾ 椭圆函数(Elliptic):存在 n 个极点,n–1 个零点,极点位于单位圆的内外侧, 零点分布在虚轴上,通带、阻带均有纹波。相比于巴特沃斯和切比雪夫函数, 椭圆函数具有更狭窄的过渡带,但是群延迟也更差。 2.3 滤波器的综合 滤波器的综合方式很多,比如:基于 RC 的综合、基于 LC 的综合以及基于 Biquad 的综合。基于 RC 的综合只能够实现实数极点,而基于 LC 的综合不适 用于集成芯片中,在这里便不作详细的叙述。本文中所涉及的综合方式,都是 基于 Biquad 结构,其中最常用的是 Tow-Thomas 和 Sallen-Key 结构。从电路 结构上来说,Sallen-Key 结构和 Tow-Thomas 结构的区别在于,Sallen-Key 结 构使用一个运放实现两个极点,而 Tow-Thomas 结构使用两个运放实现两个极 点。 对于 Sallen-Key 结构,有以下表达式成立[13]: 2 0 1212 1 ω RRCC = (2.13) 2 2 12 11 1 11 21 2 2 ( ) RC RC RC Q RC RC RC − = +− (2.14) 假设 R1=R2=R,得到: 2 0 1 2 1 ω R CC = (2.15) 221 1 112 ( ) CCC Q CCC − = +− (2.16) 如果单从功耗上进行考量,Sallen-Key 结构显然更具有优势。但是,由于 Sallen-Key 结构随工艺和温度变化较为敏感,而且在高频时易受寄生电容的影
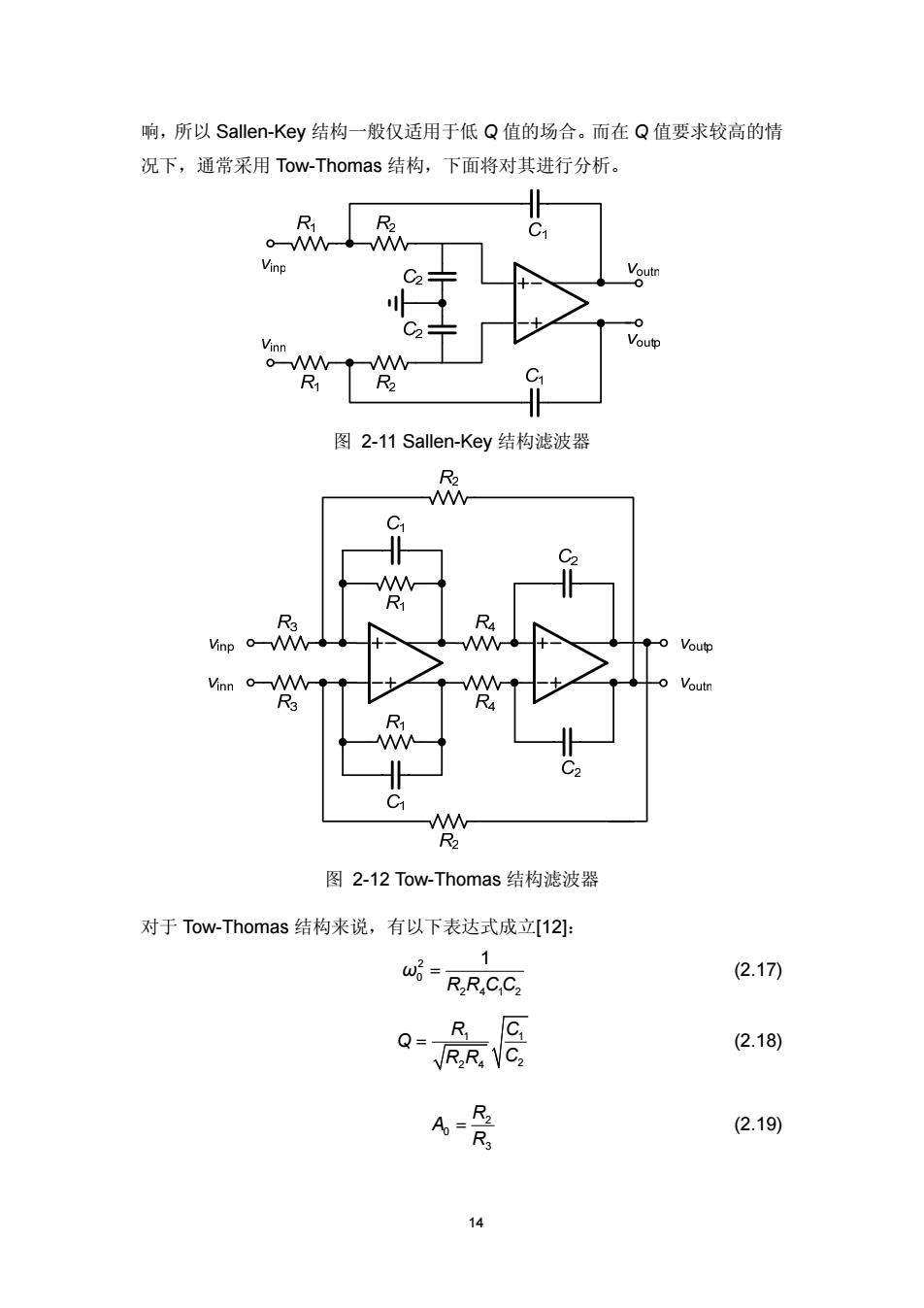
响,所以Sallen-Key结构一般仅适用于低Q值的场合。而在Q值要求较高的情 况下,通常采用Tow-Thomas结构,下面将对其进行分析。 R1 R2 C1 o◆w Vinp Voutn Vinn Voutp R R 图2-11 Sallen-Key结构滤波器 R2 W C1 C2 R R3 Vinp o 0 Voutp Vinn o Voutn R3 R R C1 W R2 图2-12Tow-Thomas结构滤波器 对于Tow-Thomas结构来说,有以下表达式成立[12]: 1 w6= (2.17) RRCC2 Q-_ R RO (2.18) Ao= R (2.19) 14
14 响,所以 Sallen-Key 结构一般仅适用于低 Q 值的场合。而在 Q 值要求较高的情 况下,通常采用 Tow-Thomas 结构,下面将对其进行分析。 图 2-11 Sallen-Key 结构滤波器 图 2-12 Tow-Thomas 结构滤波器 对于 Tow-Thomas 结构来说,有以下表达式成立[12]: 2 0 2 412 1 ω R RCC = (2.17) 1 1 2 4 2 R C Q R R C = (2.18) 2 0 3 R A R= (2.19)

做归一化,令: C1=C2=1,R2=R4=1 (2.20) 可得: R=Q,R3=1/A0 (2.21) 由以上公式可知,在Tow-Thomas结构中,滤波器的截止频率wo,Q值以及 直流增益A,都可以独立调整,各参数的设计流程如下: 1.首先根据系统要求的截止频率wo,根据噪声和面积权衡确定R和C1: 2.然后通过调整R3确定直流增益A0,确保不影响截止频率wo: 3.调整R1确定Q值,确保不影响截止频率wo和直流增益A0 2.4积分器的非理想因素 滤波器设计大部分是基于积分器的设计,下面对积分器的基本原理及其非理 想因素进行探讨[6]: R 图2-13积分器示意图 个Hs 个 0 W 0 -90 Wo 图2-14理想积分器的幅频和相频曲线 理想积分器的传递函数为: 1 H(S)=- (2.22) SRC 15
15 做归一化,令: CC R R 12 2 4 = = == 1, 1 (2.20) 可得: 1 30 R QR A = , 1/ = (2.21) 由以上公式可知,在Tow-Thomas结构中,滤波器的截止频率ω0,Q值以及 直流增益A0都可以独立调整,各参数的设计流程如下: 1. 首先根据系统要求的截止频率ω0,根据噪声和面积权衡确定RB 1B和CB 1; 2. 然后通过调整RB 3B确定直流增益A0,确保不影响截止频率ω0; 3. 调整RB 1B确定Q值,确保不影响截止频率ω0和直流增益AB 0B。 2.4 积分器的非理想因素 滤波器设计大部分是基于积分器的设计,下面对积分器的基本原理及其非理 想因素进行探讨[6]: 图 2-13 积分器示意图 H s( ) 图 2-14 理想积分器的幅频和相频曲线 理想积分器的传递函数为: 1 0 ( ) ω H s sRC s =− =− (2.22)

幅频相频响应如图2-14所示。但是实际上,积分器是一个多极点系统,增 益也不可能无限大。假设积分器的直流增益为ADc,并且含有极点wp1,wp2,wp3 直至wpn,其中wp1是由有限增益造成的,可以得到其传递函数如下所示: H(S)= Apc (2.23) (1+91+§1+§)(1+§) Wpi Wp2 Wp3 在有源滤波器中,积分器的品质因数Q是一个很重要的指标,积分器Q值 的定义为: Q(w)= Im(H(jw)) (2.24) Re(H(jw)) 积分器的相位为: p(w)=-7+tan 2 (2.25) Q(W) 当频率位于ωo附近,此时的Q值对整个滤波器的频率响应影响非常之敏感, 我们有必要对其进行分析。假设系统具有两个极点,根据(2.23)式可得: Q(ω)=- W(Wp1+Wp2) (2.26) WpWp2-W2 1 W2-ω2 (2.27 Q(w)w(w1+W2) 假设wp2>>wp1,有: 1 Wpw (2.28) Q(w)wW2 如果不考虑第二极点的影响w2→∞,则: QW)=Wo=Aoc (2.29) Wp1 如果不考虑第二极点的影响,那么在频率o处,Q值为正。根据(2.25)式,此 时积分器在ωo处相位超前于-90°,产生了相位超前现象,使得滤波器在幅度响 应上表现为增益下降,如下图示: 6
16 幅频相频响应如图 2-14 所示。但是实际上,积分器是一个多极点系统,增 益也不可能无限大。假设积分器的直流增益为 ADC,并且含有极点 ωp1,ωp2,ωp3 直至 ωpn,其中 ωp1是由有限增益造成的,可以得到其传递函数如下所示: DC p1 p2 p3 pn ( ) (1 )(1 )(1 ) (1 ) A H s sss s ωωω ω = +++ + " (2.23) 在有源滤波器中,积分器的品质因数 Q 是一个很重要的指标,积分器 Q 值 的定义为: Im( ( )) ( ) Re( ( )) H jω Q ω H jω = − (2.24) 积分器的相位为: 1 1 ( ) tan 2 () π φ ω Q ω − ⎛ ⎞ =− + ⎜ ⎟ ⎝ ⎠ (2.25) 当频率位于 ω0附近,此时的 Q 值对整个滤波器的频率响应影响非常之敏感, 我们有必要对其进行分析。假设系统具有两个极点,根据(2.23)式可得: p1 p2 2 p1 p2 ( ) ( ) ωω ω Q ω ωω ω + = − − (2.26) 2 p1 p2 p1 p2 1 () ( ) ωω ω Q ω ωω ω − = − + (2.27) 假设 ωp2>>ωp1,有: p1 p2 1 ( ) ω ω Q ω ωω = − (2.28) 如果不考虑第二极点的影响 ωp2→∞,则: 0 0 DC p1 ( ) ω Q ω A ω= = (2.29) 如果不考虑第二极点的影响,那么在频率 ω0 处,Q 值为正。根据(2.25)式,此 时积分器在 ω0处相位超前于–90o ,产生了相位超前现象,使得滤波器在幅度响 应上表现为增益下降,如下图示:
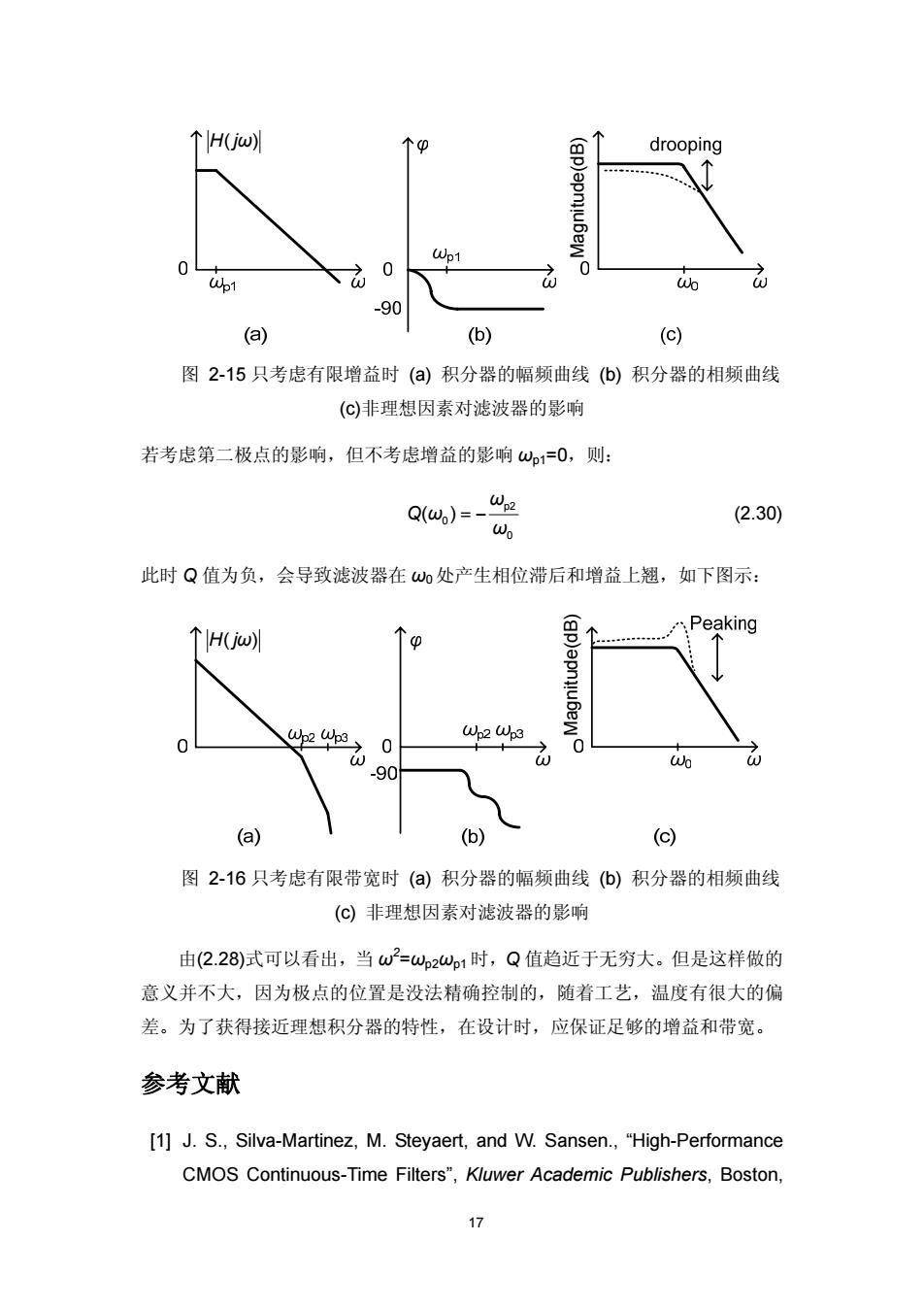
个Hjiw 个0 drooping (gp)apnu6ew Wp1 0 0 Wp1 o -90 (a) (b) (c) 图2-15只考虑有限增益时()积分器的幅频曲线(b)积分器的相频曲线 (©)非理想因素对滤波器的影响 若考虑第二极点的影响,但不考虑增益的影响w1=0,则: Q(w)=- Wp2 (2.30) W 此时Q值为负,会导致滤波器在ωo处产生相位滞后和增益上翘,如下图示: Peaking 个H(w 可 Wp2 Wp3 Wp2 Wp3 0 71 90 Wo (a) (b) (©) 图2-16只考虑有限带宽时()积分器的幅频曲线(b)积分器的相频曲线 (©)非理想因素对滤波器的影响 由(2.28)式可以看出,当w2=w2wp1时,Q值趋近于无穷大。但是这样做的 意义并不大,因为极点的位置是没法精确控制的,随着工艺,温度有很大的偏 差。为了获得接近理想积分器的特性,在设计时,应保证足够的增益和带宽。 参考文献 [1]J.S.,Silva-Martinez,M.Steyaert,and W.Sansen.,"High-Performance CMOS Continuous-Time Filters",Kluwer Academic Publishers,Boston, 17
17 H j ( ) ω Magnitude(dB) 图 2-15 只考虑有限增益时 (a) 积分器的幅频曲线 (b) 积分器的相频曲线 (c)非理想因素对滤波器的影响 若考虑第二极点的影响,但不考虑增益的影响 ωp1=0,则: p2 0 0 ( ) ω Q ω ω = − (2.30) 此时 Q 值为负,会导致滤波器在 ω0处产生相位滞后和增益上翘,如下图示: H j ( ) ω Magnitude(dB) 图 2-16 只考虑有限带宽时 (a) 积分器的幅频曲线 (b) 积分器的相频曲线 (c) 非理想因素对滤波器的影响 由(2.28)式可以看出,当 ω2 =ωp2ωp1时,Q 值趋近于无穷大。但是这样做的 意义并不大,因为极点的位置是没法精确控制的,随着工艺,温度有很大的偏 差。为了获得接近理想积分器的特性,在设计时,应保证足够的增益和带宽。 参考文献 [1] J. S., Silva-Martinez, M. Steyaert, and W. Sansen., “High-Performance CMOS Continuous-Time Filters”, Kluwer Academic Publishers, Boston