Ron R R (a) (b) 图2-2寄生电阻的影响 电阻Rn的取值一般在几十欧姆,而电容C的取值一般在几个pF之内。由 此可以估算,此零点的位置应该位于GHz之外,不会对滤波器的性能造成很大 的影响。相反,此零点会在高频处产生相位超前,可以在一定程度上补偿由于 有限带宽而导致的相位滞后[6]。如果将MOS开关管的WL取得较小,可以获 得较大的导通阻抗,使得零点位置靠近单位增益带宽,从而获得更好的频率响 应,但是这是以牺牲滤波器的线性度为代价的。 Opamp-RC滤波器的噪声贡献通常是由电阻主导的。相比与Gm-C滤波器 来说,Opamp-RC滤波器在噪声方面变现得更加优越,因为无源电阻的噪声贡 献比放大器组成的跨导要小许多。因此Opamp-RC滤波器通常应用于高动态范 围,高线性度的中低频系统中。 MOSFET-C滤波器和Opamp-RC滤波器的区别在于,MOSFET-C滤波器 用MOS管代替Opamp-RC滤波器中的电阻,其基本原理图如下: 图2-3 MOSFET-C滤波器示意图 Vc是控制信号,可以通过控制Vc获得精确的截止频率。然而MOSFET-C 8
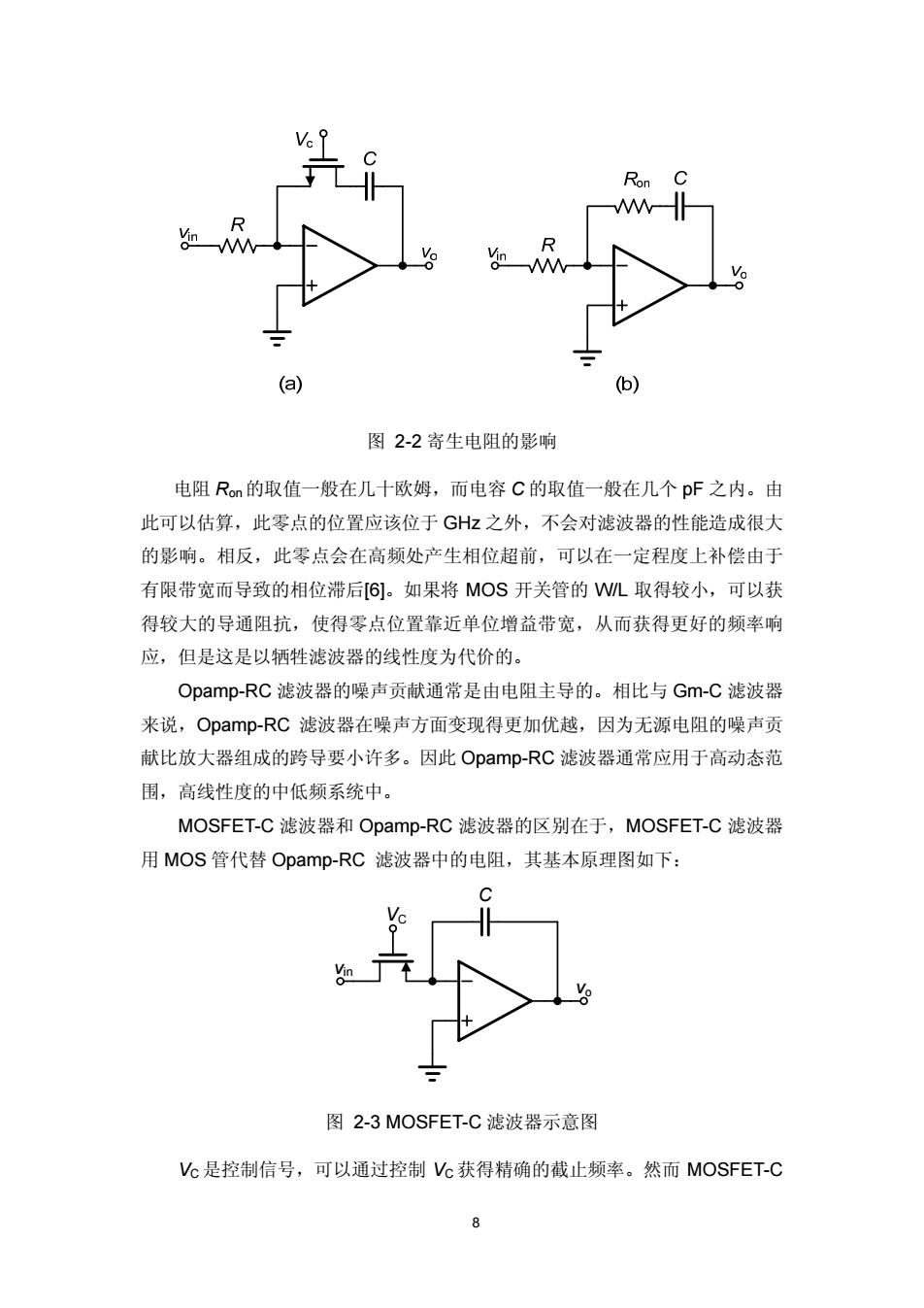
8 图 2-2 寄生电阻的影响 电阻 Ron的取值一般在几十欧姆,而电容 C 的取值一般在几个 pF 之内。由 此可以估算,此零点的位置应该位于 GHz 之外,不会对滤波器的性能造成很大 的影响。相反,此零点会在高频处产生相位超前,可以在一定程度上补偿由于 有限带宽而导致的相位滞后[6]。如果将 MOS 开关管的 W/L 取得较小,可以获 得较大的导通阻抗,使得零点位置靠近单位增益带宽,从而获得更好的频率响 应,但是这是以牺牲滤波器的线性度为代价的。 Opamp-RC 滤波器的噪声贡献通常是由电阻主导的。相比与 Gm-C 滤波器 来说,Opamp-RC 滤波器在噪声方面变现得更加优越,因为无源电阻的噪声贡 献比放大器组成的跨导要小许多。因此 Opamp-RC 滤波器通常应用于高动态范 围,高线性度的中低频系统中。 MOSFET-C 滤波器和 Opamp-RC 滤波器的区别在于,MOSFET-C 滤波器 用 MOS 管代替 Opamp-RC 滤波器中的电阻,其基本原理图如下: vin vo C VC 图 2-3 MOSFET-C 滤波器示意图 VC 是控制信号,可以通过控制 VC 获得精确的截止频率。然而 MOSFET-C
的缺点在于,其电阻实现采用MOS管实现,输入信号的变化对MOS管的线性 度会产生很大的影响,为了抑制偶数阶失真,滤波器采用全差分结构。全差分 MOSFET-C滤波器如图2-4所示, C VN Q V 0 2 VOF 图2-4全差分MOSFET-C滤波器示意图 M1 石1 2 VON VIN i2. 2 23 M2 图2-5全差分MOSFET-C滤波器的改进 由MOS管的-V曲线关系得: 6=c义。--2%s (2.3) W VIN)VIN 1o1=(Vos -Vm-4)2 (2.4) 9
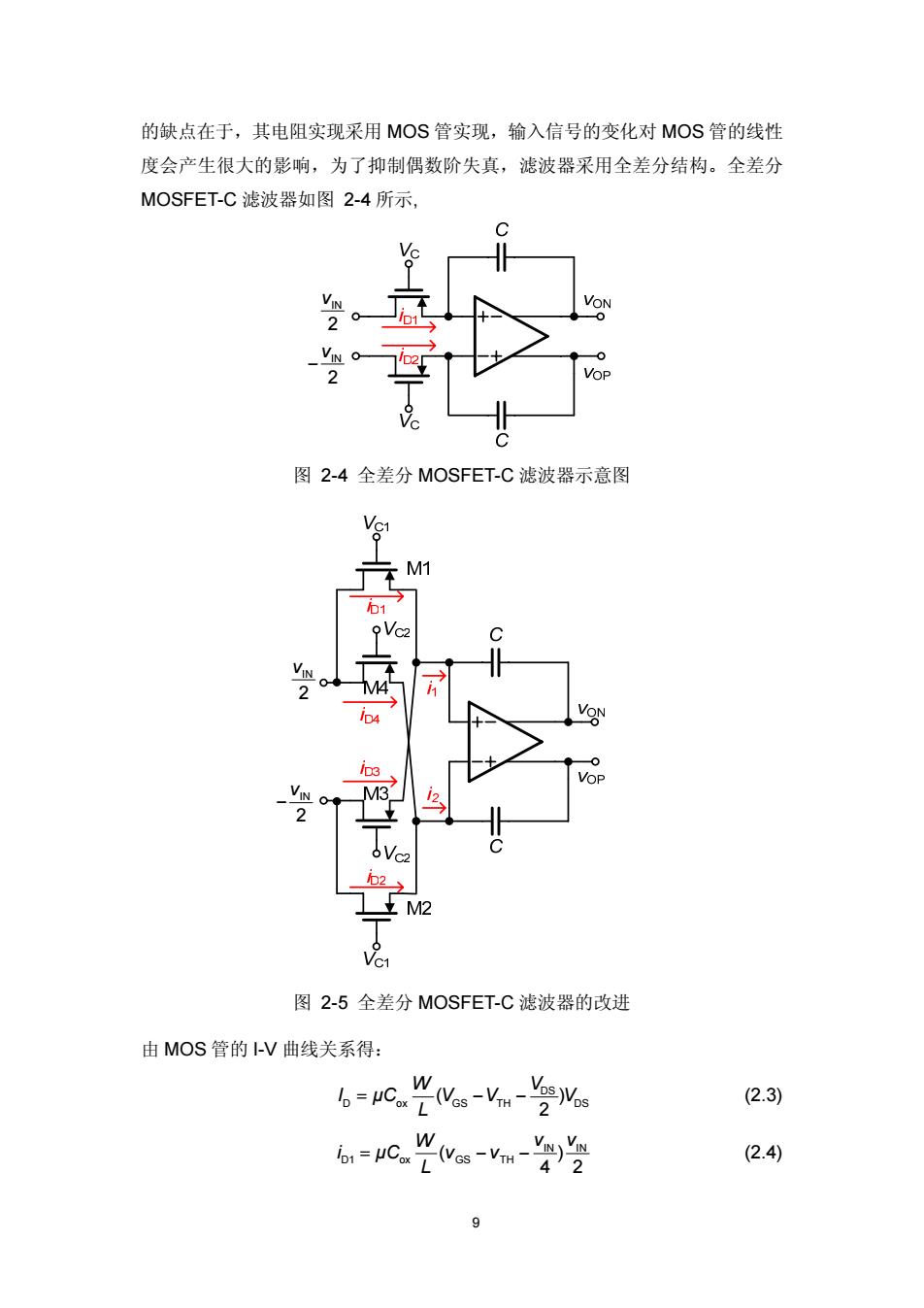
9 的缺点在于,其电阻实现采用 MOS 管实现,输入信号的变化对 MOS 管的线性 度会产生很大的影响,为了抑制偶数阶失真,滤波器采用全差分结构。全差分 MOSFET-C 滤波器如图 2-4 所示, IN 2 v IN 2 v − 图 2-4 全差分 MOSFET-C 滤波器示意图 IN 2 v IN 2 v − 图 2-5 全差分 MOSFET-C 滤波器的改进 由 MOS 管的 I-V 曲线关系得: DS D ox GS TH DS ( ) 2 W V I μC VV V L = −− (2.3) IN IN D1 ox GS TH ( ) 4 2 W v v i μC vv L = −− (2.4)

a=-c光es-m+g学 (2.5) W Vo1-o2=HC.(Vas-Vru)ViN (2.6) G-o-io-uCW(Vas-Vm) W (2.7) OVIN 由(2.7)式知,电路的非线性被消除了。实际上,阈值电压VH也是随着输入信 号而变化的,这将在一定程度上限制MOSFET-C滤波器的线性度。为了克服电 路对阈值电压的依赖性,又提出了新的电路结构如图2-5[7]。 4=6+ia=cYes1-ea学2 (2.8) 272 W VIN)VIN a os +/o2 UCoxL(Vos3 -Vos1-2)2 (2.9) h-h-pC_W(Veu-VooWa (2.10) g--cYes-a-eY4-a) (2.11) OVIN 由(2.11)式可以看出,改进的OTA-C滤波器得到了独立于阈值电压的跨导, 这将使得其线性度性能进一步提升。在MOSFET-C滤波器中,MOS开关管的 栅极电压需要足够大以提供好的线性度性能,因此经常采用Charge Pump技术 来提升栅极电压。和Opamp-RC滤波器相比,MOSFET-C滤波器的噪声性能与 之相仿,但是由于MOS管的使用,使得其高频性能不如Opamp-RC优越。 2.1.2Gm-C滤波器 G-C滤波器更多的应用于中高频系统中,它采用开环架构,不存在稳定性 问题[8],在面积和功耗方面表现优越。但正是由于采用开环结构,使得它的线 性度不好,而且输入信号范围严重受限[1)[4]。 Gm 图2-6Gm-C滤波器示意图 10
10 IN IN D2 ox GS TH ( ) 4 2 W v v i μC vv L =− − + (2.5) D1 D2 ox GS TH IN ( ) W i i μC v vv L −= − (2.6) D1 D2 ox GS TH IN ( ) ( ) i i W G μC vv v L ∂ − == − ∂ (2.7) 由(2.7)式知,电路的非线性被消除了。实际上,阈值电压 VTH 也是随着输入信 号而变化的,这将在一定程度上限制 MOSFET-C 滤波器的线性度。为了克服电 路对阈值电压的依赖性,又提出了新的电路结构如图 2-5 [7]。 IN IN 1 D1 D3 ox GS1 GS3 ( ) 2 2 W v v ii i μC vv L =+= − − (2.8) IN IN 2 D4 D2 ox GS3 GS1 ( ) 2 2 W v v ii i μC vv L =+= − − (2.9) 1 2 ox GS1 GS3 IN ( ) W i i μC v vv L −= − (2.10) 1 2 ox GS1 GS3 ox C1 C2 IN ( ) ( ) () i i W W G μC vv μC VV vL L ∂ − = = −= − ∂ (2.11) 由(2.11)式可以看出,改进的 OTA-C 滤波器得到了独立于阈值电压的跨导, 这将使得其线性度性能进一步提升。在 MOSFET-C 滤波器中,MOS 开关管的 栅极电压需要足够大以提供好的线性度性能,因此经常采用 Charge Pump 技术 来提升栅极电压。和 Opamp-RC 滤波器相比,MOSFET-C 滤波器的噪声性能与 之相仿,但是由于 MOS 管的使用,使得其高频性能不如 Opamp-RC 优越。 2.1.2 Gm-C 滤波器 Gm-C 滤波器更多的应用于中高频系统中,它采用开环架构,不存在稳定性 问题[8],在面积和功耗方面表现优越。但正是由于采用开环结构,使得它的线 性度不好,而且输入信号范围严重受限[1] [4]。 图 2-6 Gm-C 滤波器示意图

图2-6中给出了Gm-C滤波器的示意图,其传递函数如下: Hs)=- (2.12) sC Gm-C滤波器中的跨导Gm由OTA实现,随工艺变化较大,需要进行频率 校准。Gm-C滤波器的校准通常采用PLL环路来实现。为了改善Gm-C滤波器 的线性度,会在OTA的输入级采用一些线性化技术,常见的方法有: 1.利用线性区MOS管做输入源极退化电阻[9]: 2.利用线性区的MOS管作为输入管[10]: 3.利用源极跟随器作浮接电压以改善跨导放大器的线性度[10]。 6 M1 M3 LM4 VSS 图2-7线性区MOS管做输入源极退化电阻的跨导放大器 M 2 图2-8线性区的MOS管作输入管跨导放大器 11
11 图 2-6 中给出了 Gm-C 滤波器的示意图,其传递函数如下: m ( ) G H s sC = − (2.12) Gm-C 滤波器中的跨导 Gm 由 OTA 实现,随工艺变化较大,需要进行频率 校准。Gm-C 滤波器的校准通常采用 PLL 环路来实现。为了改善 Gm-C 滤波器 的线性度,会在 OTA 的输入级采用一些线性化技术,常见的方法有: 1. 利用线性区 MOS 管做输入源极退化电阻[9]; 2. 利用线性区的 MOS 管作为输入管[10]; 3. 利用源极跟随器作浮接电压以改善跨导放大器的线性度[10]。 图 2-7 线性区 MOS 管做输入源极退化电阻的跨导放大器 图 2-8 线性区的 MOS 管作输入管跨导放大器
学n:学加学a学u=1nn:1 op M2 n+1)) 图2-9源极跟随器作浮接电压的跨导放大器 2.2滤波器的函数实现 个lm(s) 个lm(s) Re(s) Re(s) (a) (b) 个lm(s) 个lm(s) Re(s) X Re(s) N (c) (d) 图2-10(a)巴特沃斯函数(b)切比雪夫函数(c)反切比雪夫函数(d椭圆函数 滤波器的函数实现主要包括:巴特沃斯函数、切比雪夫函数、反切比雪夫函 数和椭圆滤波器等。图2-10中分别给出了四种函数的零极点分布图,下面对它 们做简单的介绍[12]: >巴特沃斯函数(Butterworth):全极点系统,极点均匀的分布在单位圆上,通 12
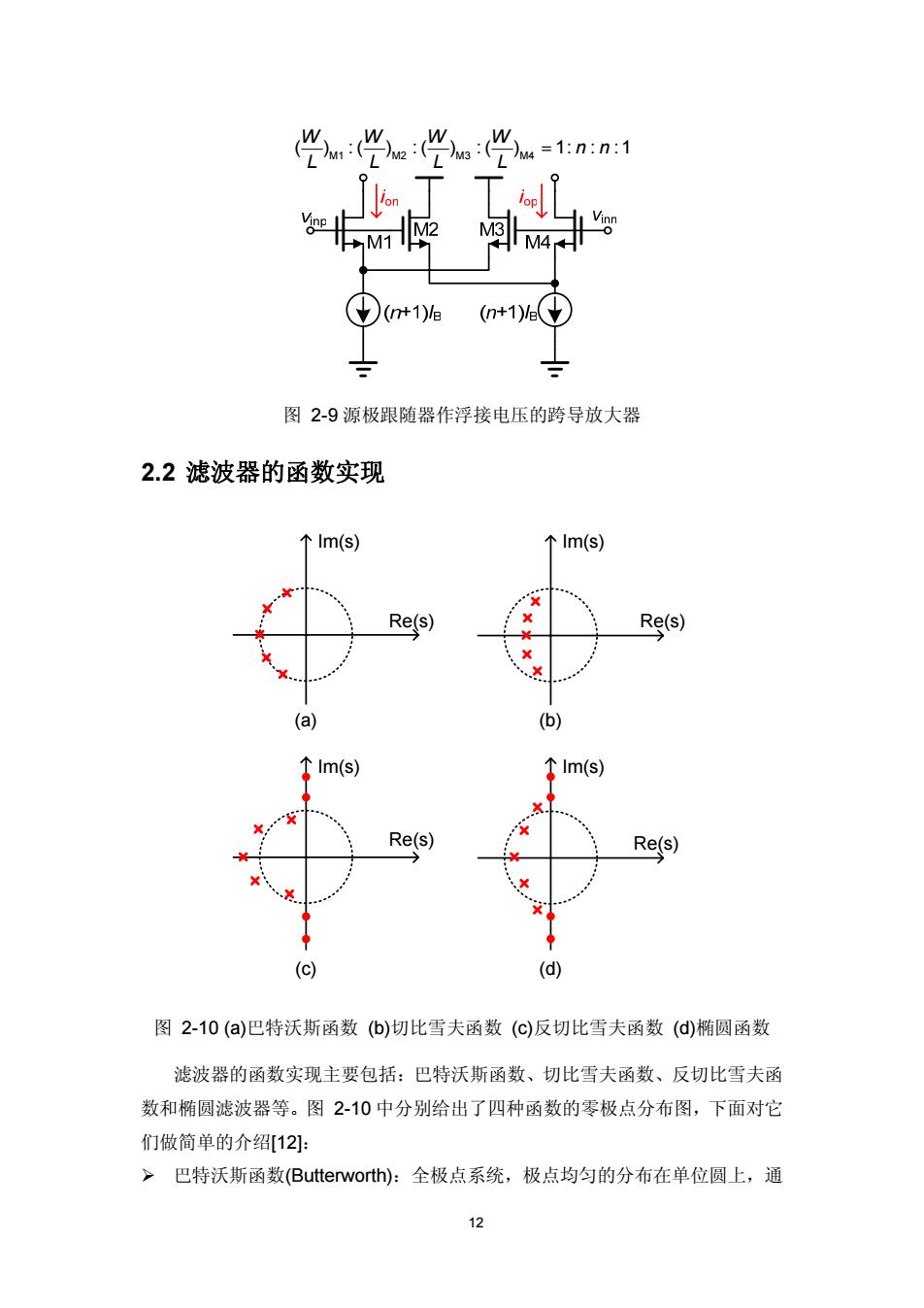
12 M1 M2 M3 M4 ( ) :( ) :( ) :( ) 1: : :1 WWWW n n LLLL = 图 2-9 源极跟随器作浮接电压的跨导放大器 2.2 滤波器的函数实现 Im(s) Re(s) Im(s) Re(s) Im(s) Re(s) Im(s) Re(s) (a) (b) (c) (d) 图 2-10 (a)巴特沃斯函数 (b)切比雪夫函数 (c)反切比雪夫函数 (d)椭圆函数 滤波器的函数实现主要包括:巴特沃斯函数、切比雪夫函数、反切比雪夫函 数和椭圆滤波器等。图 2-10 中分别给出了四种函数的零极点分布图,下面对它 们做简单的介绍[12]: ¾ 巴特沃斯函数(Butterworth):全极点系统,极点均匀的分布在单位圆上,通