
本次课主要内容 平面性算法 (一)、涉及算法的相关概念 (二)、平面性算法
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、涉及算法的相关概念 (二)、平面性算法 平面性算法

(一)、涉及算法的相关概念 关于图的平面性问题,我们已经建立了一些平面性 判定方法: (1)对于简单图G=(n,m),如果m>3n-6,则G是非可 平面的; (2)对于简单连通图G=(m,),如果每个面次数至少 为23,且m>(m-2)11-2),则G是非可平面的; ③)库拉托斯基定理:G是可平面的当且仅当G不含有 与K和K3.3同胚的子图 (4)瓦格纳定理:G是可平面的当且仅当G不含有能够 收缩成K和K33的子图;
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 关于图的平面性问题,我们已经建立了一些平面性 判定方法: (一)、涉及算法的相关概念 (1) 对于简单图G=(n, m),如果m>3n-6,则G是非可 平面的; (2) 对于简单连通图G=(n, m),如果每个面次数至少 为l≥3,且m>(n-2)l /(l-2),则G是非可平面的; (3) 库拉托斯基定理:G是可平面的当且仅当G不含有 与K5和K3,3同胚的子图; (4) 瓦格纳定理:G是可平面的当且仅当G不含有能够 收缩成K5和K3,3的子图;
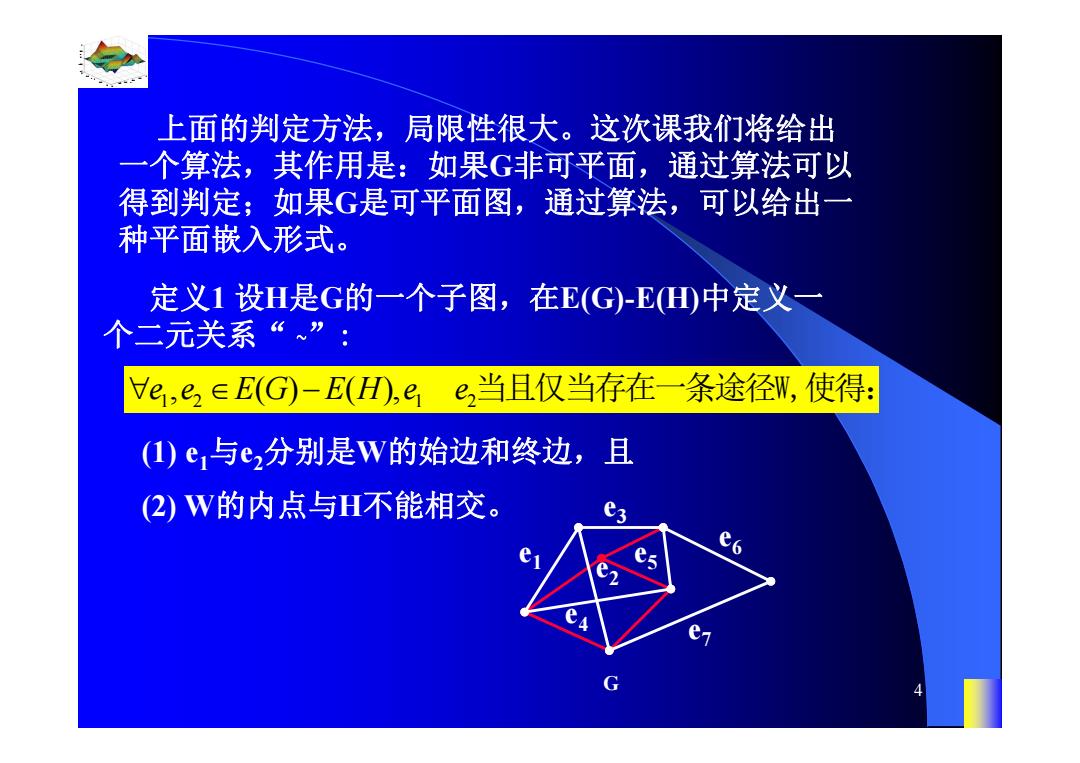
上面的判定方法,局限性很大。这次课我们将给出 一个算法,其作用是:如果G非可平面,通过算法可以 得到判定;如果G是可平面图,通过算法,可以给出一 种平面嵌入形式。 定义1设H是G的一个子图,在E(G)-E山中定义一 个二元关系“、”: e,e,∈E(G)-E(H,ee,当且仅当存在一条途径W,使得: (I)e,与e2分别是W的始边和终边,且 (2)W的内点与H不能相交。 e e
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 上面的判定方法,局限性很大。这次课我们将给出 一个算法,其作用是:如果G非可平面,通过算法可以 得到判定;如果G是可平面图,通过算法,可以给出一 种平面嵌入形式。 定义1 设H是G的一个子图,在E(G)-E(H)中定义一 个二元关系“ ~”: 12 1 2 e e EG EH e e , ( ) ( ), 当且仅当存在一条途径W,使得: (1) e1与e2分别是W的始边和终边,且 (2) W的内点与H不能相交。 G e4 e3 e2 e1 e7 e6 e5
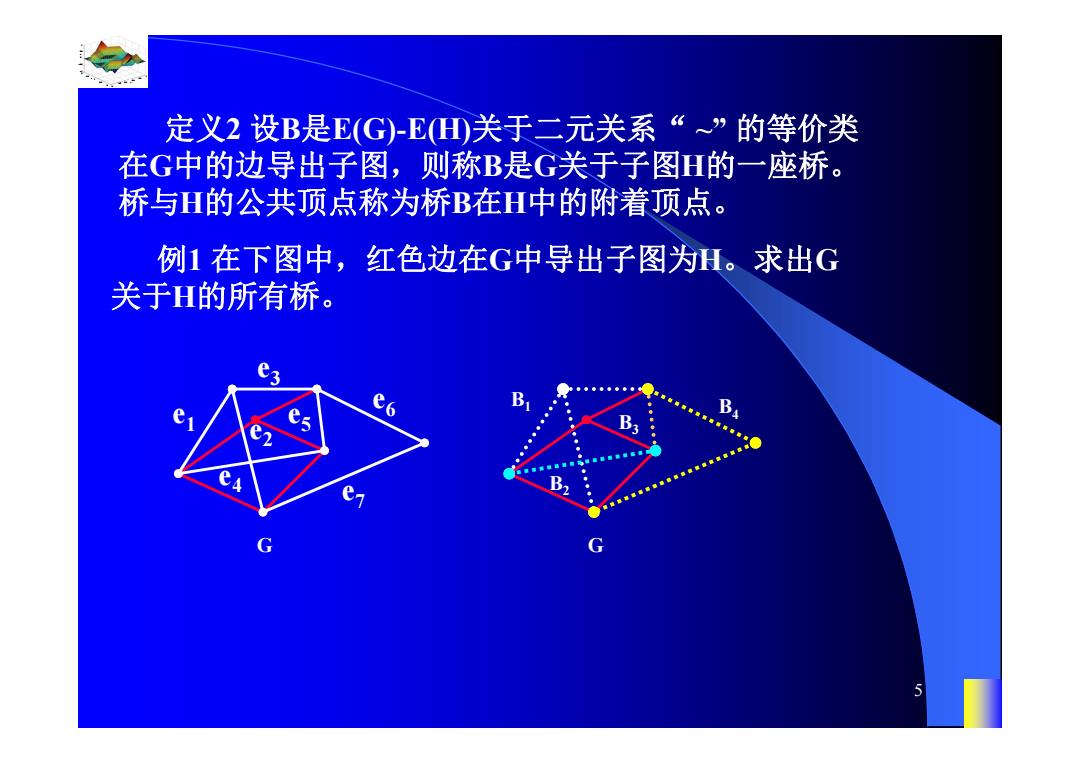
定义2设B是E(G)-E山D关于二元关系“”的等价类 在G中的边导出子图,则称B是G关于子图的一座桥。 桥与H的公共顶点称为桥B在H中的附着顶点。 例1在下图中,红色边在G中导出子图为H。求出G 关于H的所有桥。 e e 4
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义2 设B是E(G)-E(H)关于二元关系“ ~” 的等价类 在G中的边导出子图,则称B是G关于子图H的一座桥。 桥与H的公共顶点称为桥B在H中的附着顶点。 例1 在下图中,红色边在G中导出子图为H。求出G 关于H的所有桥。 G B1 B2 B3 B4 G e4 e3 e2 e1 e7 e6 e5
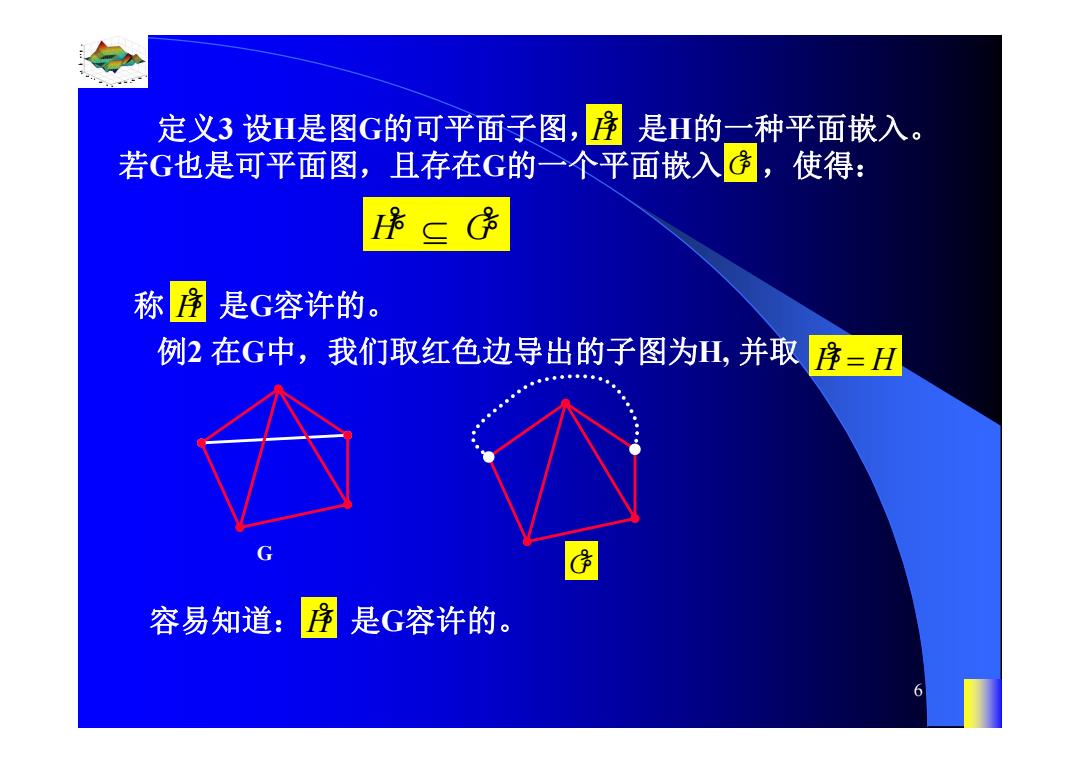
定义3设H是图G的可平面子图,序是H的一种平面嵌入。 若G也是可平面图,且存在G的一个平面嵌入,使得: 称序 是G容许的。 例2在G中,我们取红色边导出的子图为H,并取序=H 容易知道:序是G容许的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义3 设H是图G的可平面子图, 是H的一种平面嵌入。 若G也是可平面图,且存在G的一个平面嵌入 ,使得: 称 是G容许的。 H% G% H G % % H% 例2 在G中,我们取红色边导出的子图为H, 并取 H% H 容易知道: 是G容许的。 G G% H%