
本次课主要内容 期末复习 (一)、重点概念 (二)、重要结论 (三)、应用
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (二)、重要结论 期末复习 (一)、重点概念 (三)、应用

(一)、重点概念 1、图、简单图、图的同构与自同构、度序列与图序列、 补图与自补图、两个图的联图、两个图的积图、偶图; (1)图:一个图是一个序偶<V,E>,记为G=(V,E),其中: 1)V是一个有限的非空集合,称为顶点集合,其元素称为顶点或点。 用|V表示顶点数; 2)E是由V中的点组成的无序对构成的集合,称为边集,其元素称 为边,且同一点对在卫中可以重复出现多次。用E表示边数。 (2)简单图:无环无重边的图称为简单图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 (一)、重点概念 1、图、简单图、图的同构与自同构、度序列与图序列、 补图与自补图、两个图的联图、两个图的积图、偶图; (1) 图:一个图是一个序偶<V,E>,记为G=(V,E),其中: 1) V是一个有限的非空集合,称为顶点集合,其元素称为顶点或点。 用|V|表示顶点数; 2) E是由V中的点组成的无序对构成的集合,称为边集,其元素称 为边,且同一点对在E中可以重复出现多次。用|E|表示边数。 (2) 简单图:无环无重边的图称为简单图

(3) 图的度序列: 一个图G的各个点的度d,d2,,dn构成的非负整数组(d,d2,,dn) 称为G的度序列。 注:度序列的判定问题是重点。 (4图的图序列: 一个非负数组如果是某简单图的度序列,我们称它为可图序列,简 称图序列。 注:图序列的判定问题是重点。 (⑤)图的同构:
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 (3) 图的度序列: 一个图G的各个点的度d1, d2,…, dn构成的非负整数组(d1, d2,…, dn) 称为G的度序列 。 注:度序列的判定问题是重点。 (4) 图的图序列: 一个非负数组如果是某简单图的度序列,我们称它为可图序列,简 称图序列。 注:图序列的判定问题是重点。 (5) 图的同构:

设有两个图G=(V,E)和G2=(V2,E2),若在其顶点集合间存在双射,使得边 之间存在如下关系:设u1→u2Y1→V2,u1∈V1,u2,Y2∈V2uV1∈E1,当 且仅当u2Y2∈E2,且uV,与u2Y2的重数相同。称G,与G2同构,记为: G1¥G2 例1指出4个顶点的非同构的所有简单图。 分析:四个顶点的简单图最少边数为0,最多边数为6,所以 可按边数进行枚举。 11
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 设有两个图G1=(V1,E1)和G2=(V2,E2),若在其顶点集合间存在双射,使得边 之间存在如下关系:设u1↔u2v1↔v2, u1,v1 V1, u2,v2 V2; u1v1 E1,当 且仅当u2v2 E2 ,且u1v1与u2v2的重数相同。称G1与G2同构,记为: G G 1 2 例1 指出4个顶点的非同构的所有简单图。 分析:四个顶点的简单图最少边数为0,最多边数为6,所以 可按边数进行枚举
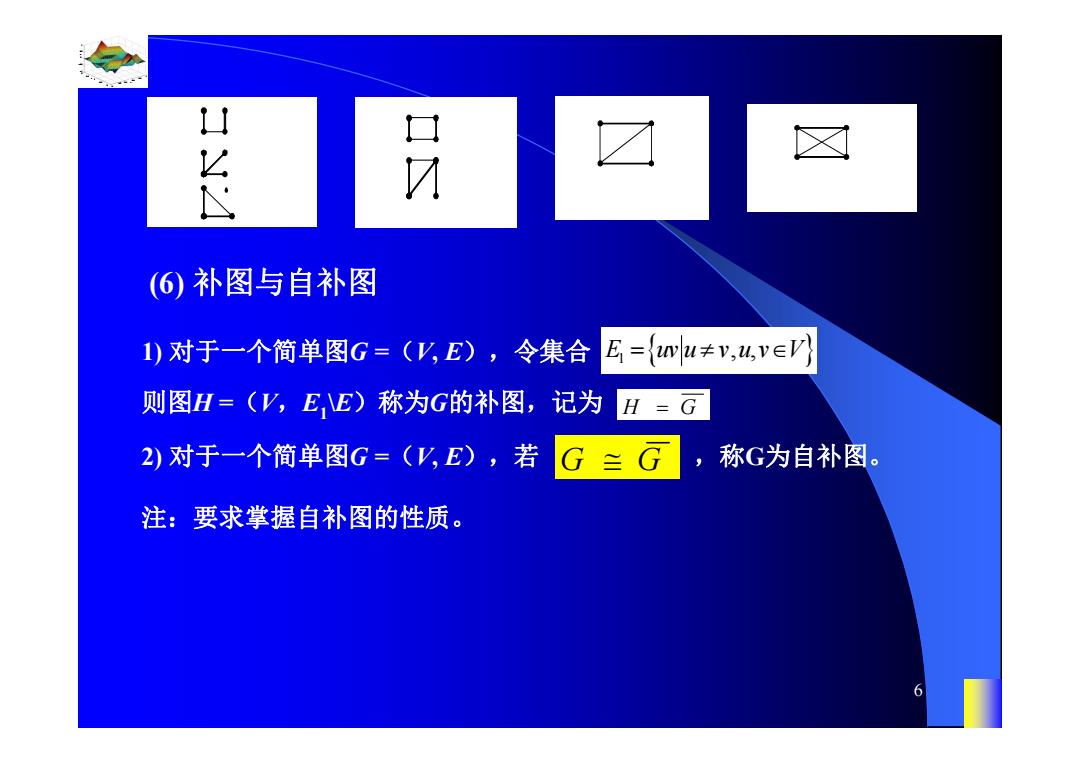
山 ∠ 口7 (6)补图与自补图 1)对于一个简单图G=(V,E),令集合 E={wlu≠v,4,v∈V旷 则图H=(V,EE)称为G的补图,记为H=G 2)对于一个简单图G=(V,E),若 G G, 称G为自补图。 注:要求掌握自补图的性质。 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 (6) 补图与自补图 1) 对于一个简单图G =(V, E),令集合 E1 uv u v u v V , , 则图H =(V,E1\E)称为G的补图,记为 H G 2) 对于一个简单图G =(V, E),若 ,称 G G G为自补图。 注:要求掌握自补图的性质