
本次课主要内容 托特定理与图的因子分解 (一)、托特定理 (二)、图的一因子分解 (三)、图的二因子分解 (四)、图的森林因子分解
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (二)、图的一因子分解 (三)、图的二因子分解 (四)、图的森林因子分解 托特定理与图的因子分解 (一)、托特定理

(三)、托特定理 定理(托特定理,1947) 图G有完美匹配当且仅当对V 的任意非空真子集S,有: o(G-S)≤lS 注:0(G-S)表示奇分支数目
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 (三)、托特定理 定理 (托特定理,1947) 图G有完美匹配当且仅当对V 的任意非空真子集S, 有: oG S S ( ) 注:o (G-S)表示奇分支数目

例1证明:一棵树G有完美匹配当且仅当对所有顶点y ∈G,有:0(G-v)=1。 证明:“必要性” 一方面:若G有完美匹配,由托特定理:0(G-v)≤1 另一方面:若树G有完美匹配,则显然G为偶阶树,于是 o(G-v)≥1; 所以:o(G-v)=1。 “充分性” 由于对任意点v∈V(G),有o(G-v)户1
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 例1 证明:一棵树G有完美匹配当且仅当对所有顶点v ∈V(G),有:o (G - v)=1。 证明:“必要性” 一方面:若G有完美匹配,由托特定理:o(G-v)≦1; 另一方面:若树G有完美匹配,则显然G为偶阶树,于是 o(G-v)≥1; 所以:o(G-v)=1。 “充分性” 由于对任意点v ∈V(G), 有o(G-v)=1
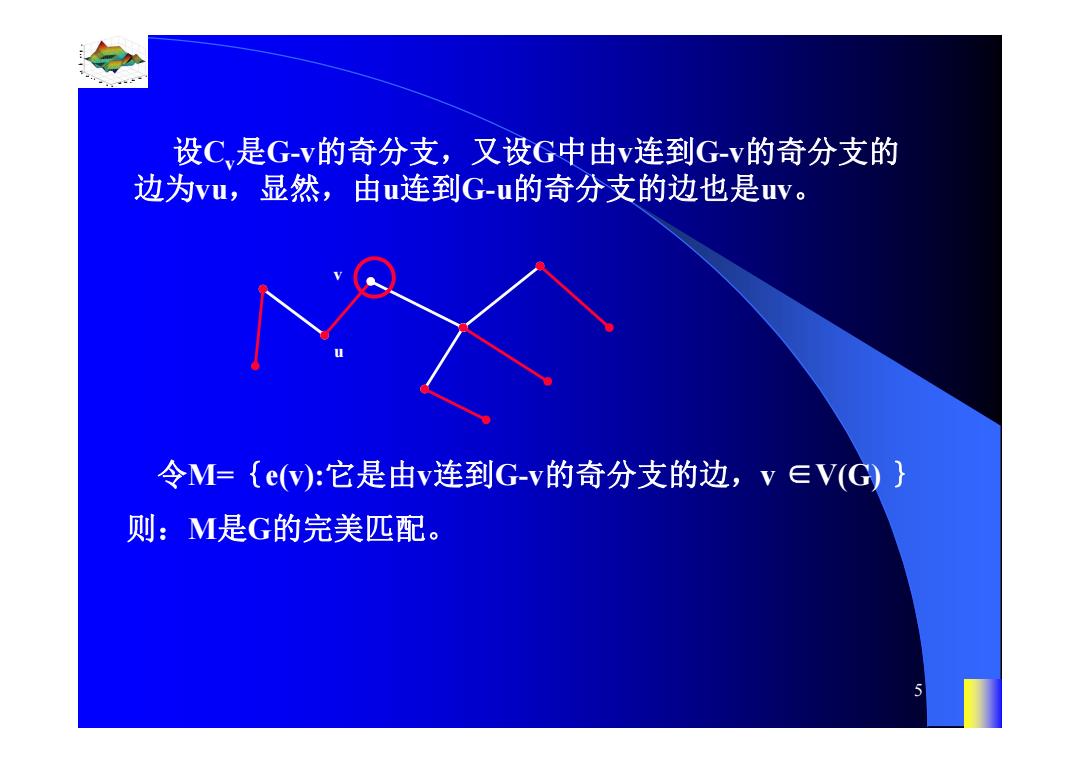
设C是G-v的奇分支,又设G中由v连到G-v的奇分支的 边为vu,显然,由u连到G-u的奇分支的边也是uy。 令M={e(w):它是由v连到G-v的奇分支的边,v∈V(G) 则:M是G的完美匹配
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 设Cv是G-v的奇分支,又设G中由v连到G-v的奇分支的 边为vu,显然,由u连到G-u的奇分支的边也是uv。 令M={e(v):它是由v连到G-v的奇分支的边,v ∈V(G) } 则:M是G的完美匹配。 v u
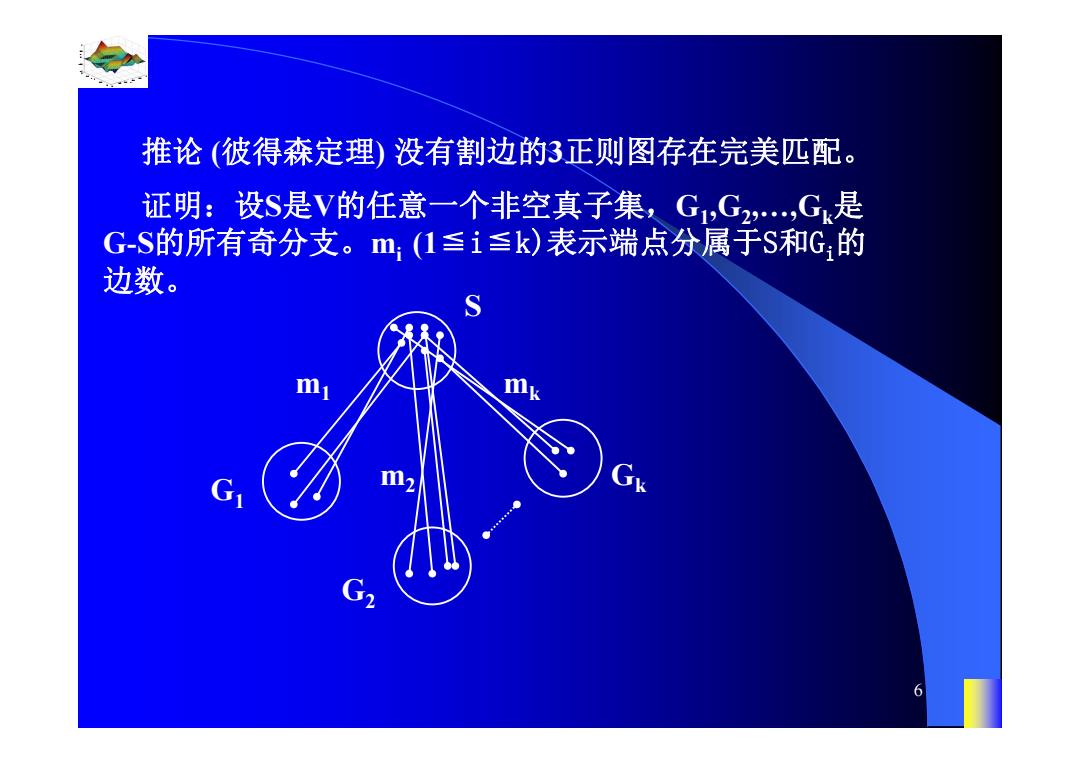
推论(彼得森定理)没有割边的3正则图存在完美匹配。 证明:设S是V的任意一个非空真子集,G1,G2,G是 G-S的所有奇分支。m,(1≤i≤k)表示端点分属于S和G:的 边数。 m G 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 推论 (彼得森定理) 没有割边的3正则图存在完美匹配。 证明:设S是V的任意一个非空真子集,G1,G2,…,Gk是 G-S的所有奇分支。mi (1≦i≦k)表示端点分属于S和Gi的 边数。 S G1 G2 Gk m1 m2 mk