
本次课主要内容 偶图的匹配问题 (一)、: 图的匹配与贝尔热定理 (二)、偶图的匹配与覆盖
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、图的匹配与贝尔热定理 (二)、偶图的匹配与覆盖 偶图的匹配问题

关于偶图的基础回顾 1、定义:所谓具有二分类(X,Y的偶图(或二部图)是 指一个图,它的点集可以分解为两个(非空)子集X和Y,使得 每条边的一个端点在X中,另一个端点在中. 注:1、偶图不能有环,偶图可以有重边; 2、偶图刻画的是两类事物之间的某种联系状态
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 关于偶图的基础回顾 1、定义:所谓具有二分类(X, Y)的偶图(或二部图)是 指一个图,它的点集可以分解为两个(非空)子集X和Y,使得 每条边的一个端点在X中,另一个端点在Y中. A G B C D E F a b c d efg 注:1、偶图不能有环,偶图可以有重边; 2、偶图刻画的是两类事物之间的某种联系状态

2、k-正则偶图 每个顶点度数均为k的偶图称为k-正则偶图。 2-正则偶图 性质:k-正则偶图的两个顶点子集包含顶点个数相等 3、图G是偶图当且仅当G不含奇圈【判定定理】
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 2、k-正则偶图 每个顶点度数均为k的偶图称为k-正则偶图。 2-正则偶图 性质:k-正则偶图的两个顶点子集包含顶点个数相等。 3、图G是偶图当且仅当G不含奇圈【判定定理】
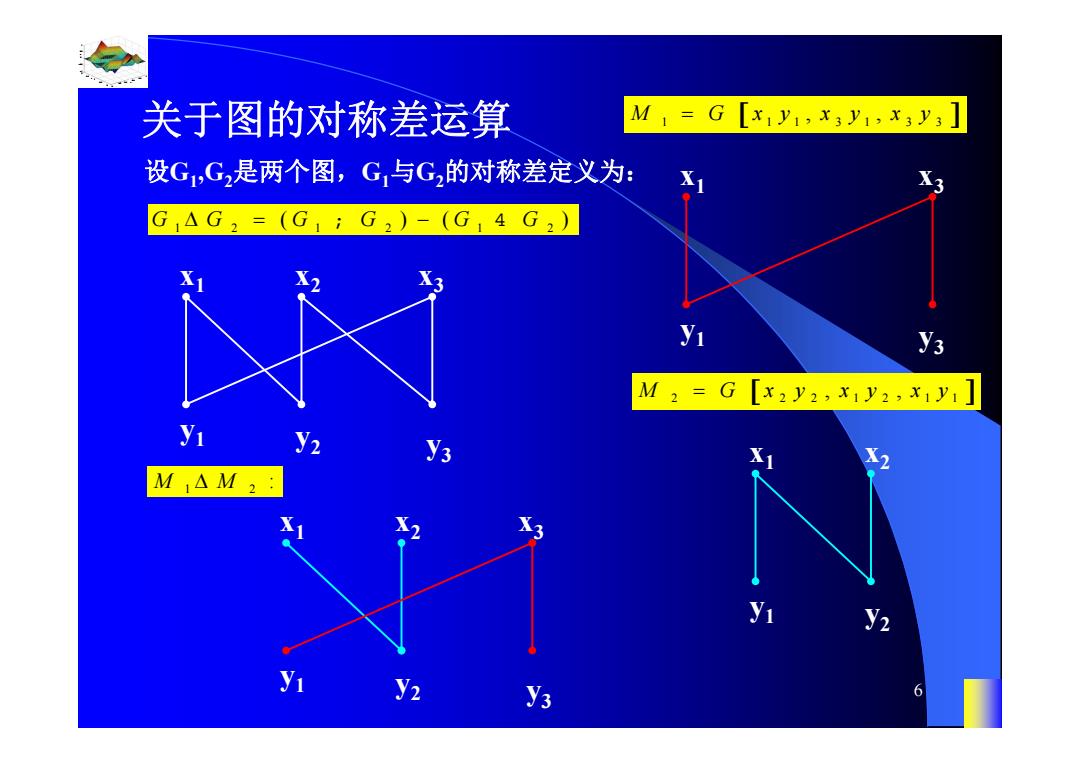
关于图的对称差运算 M1=G[x1y1,x3y1,x;y3] 设G1,G,是两个图,G,与G的对称差定义为: G,△G2=(G1;G2)-(G14G2) M2=G[x2y2,x1y2,x1y1] Y1 y2 Y3 M1△M2: y2 y y2 Ve 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 关于图的对称差运算 设G1,G2是两个图,G1与G2的对称差定义为: 12 1 2 1 2 GG G G G G ( )( ) U I y3 y2 y1 x1 x2 x3 M 1 11 31 3 3 G xy xy xy , , M 2 2 2 1 2 11 G x y xy xy , , y1 x1 x3 y3 y2 y1 x1 x2 y3 y2 y1 x1 x2 x3 1 2 M M :

(一)、 图的匹配与贝尔热定理 1、图的匹配相关概念 (1)、匹配M-如果M是图G的边子集(不含环),且 M中的任意两条边没有共同顶点,则称M是G的一个匹 配或对集或边独立集。 如果G中顶点v是G的匹配M中某条边的端点,称它 为M饱和点,否则为M非饱和点。 M={vov-} M=VoV7,VIVs} M3={VGV7,VIVs,V3V4} M1,M2,M3等都是G的匹配
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 1、图的匹配相关概念 (1)、匹配 M--- 如果M是图G的边子集(不含环),且 M中的任意两条边没有共同顶点,则称M是G的一个匹 配或对集或边独立集。 (一)、图的匹配与贝尔热定理 如果G中顶点v是G的匹配 M中某条边的端点,称它 为M饱和点,否则为M非饱和点。 v1 v7 v6 G v8 v2 v3 v5 v4 M1={v6v7} M2={v6v7, v1v8} M3={v6v7, v1v8, v3v4} M1,M2,M3等都是G的匹配