
本次课主要内容 图的顶点着色 (一)、相关概念 (二)、图的点色数的几个结论 (三)、四色与五色定理 (四)、顶点着色的应用
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、相关概念 (二)、图的点色数的几个结论 (三)、四色与五色定理 图的顶点着色 (四)、顶点着色的应用

(一)、相关概念 跟图的边着色问题一样,生活中的很多问题,也可以 模型为所谓的图的顶点着色问题来处理。例如课程安排 问题。 课程安排问题:某大学数学系要为这个夏季安排课程 表。所要开设的课程为:图论(GT),统计学(S),线性代数 LA),高等微积分(AC),几何学(G),和近世代数MA)。现 有10名学生(如下所示)需要选修这些课程。根据这些信息, 确定开设这些课程所需要的最少时间段数,使得学生选 课不会发生冲突。(学生用A表示) A:LA,S;A2:MA,LA,G;A3:MA,G,LA; A:G,LA,AC;As:AC,LA,S;A:G,AC; Az:GT,MA,LA;As:LA,GT,S;A:AC,S,LA;A10:GT,S
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 跟图的边着色问题一样,生活中的很多问题,也可以 模型为所谓的图的顶点着色问题来处理。例如课程安排 问题。 (一)、相关概念 课程安排问题:某大学数学系要为这个夏季安排课程 表。所要开设的课程为:图论(GT), 统计学(S),线性代数 (LA), 高等微积分(AC), 几何学(G), 和近世代数(MA)。现 有10名学生(如下所示)需要选修这些课程。根据这些信息, 确定开设这些课程所需要的最少时间段数,使得学生选 课不会发生冲突。(学生用Ai表示) A1: LA, S ; A2: MA, LA, G ; A3: MA, G, LA; A4: G, LA, AC ; A5: AC, LA, S ; A6: G, AC; A7: GT, MA, LA ; A8: LA,GT, S ; A9: AC, S, LA; A10: GT, S

把课程模型为图G的顶点,两顶点连线当且仅当有某 个学生同时选了这两门课程。 GT MA AC 选课状态图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 把课程模型为图G的顶点,两顶点连线当且仅当有某 个学生同时选了这两门课程。 GT MA G AC LA S 选课状态图
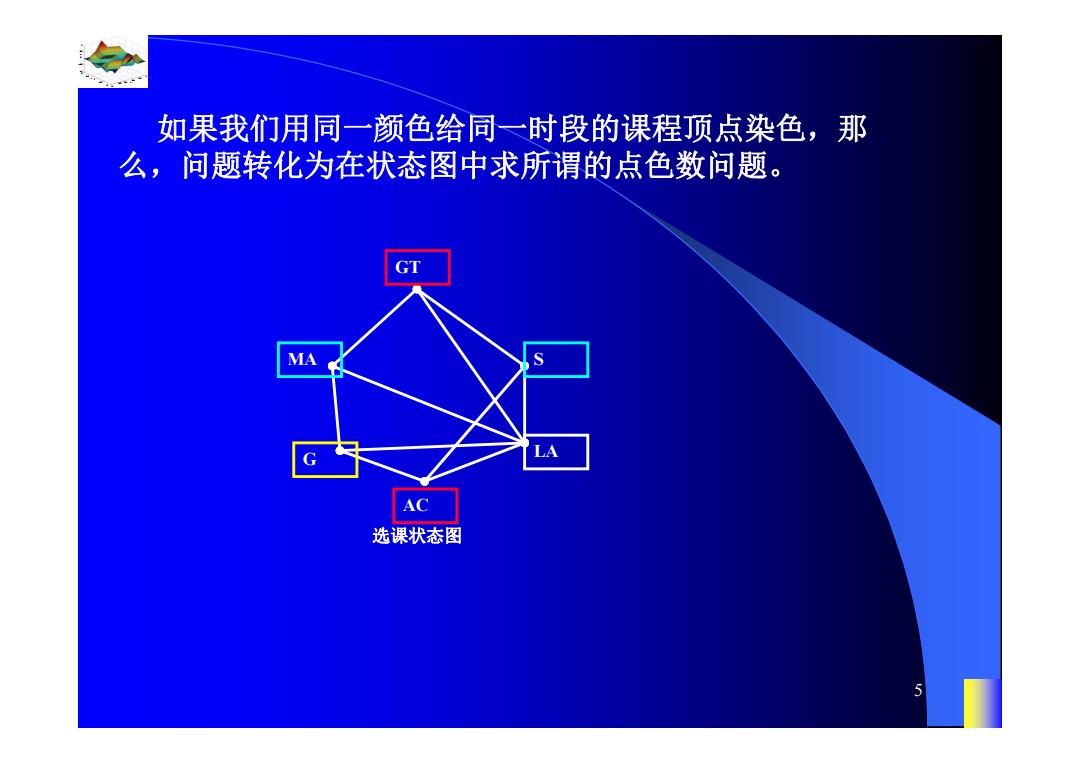
如果我们用同一颜色给同二时段的课程顶点染色,那 么,问题转化为在状态图中求所谓的点色数问题。 GT MA LA AC 选课状态图
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 如果我们用同一颜色给同一时段的课程顶点染色,那 么,问题转化为在状态图中求所谓的点色数问题。 GT MA G AC LA S 选课状态图
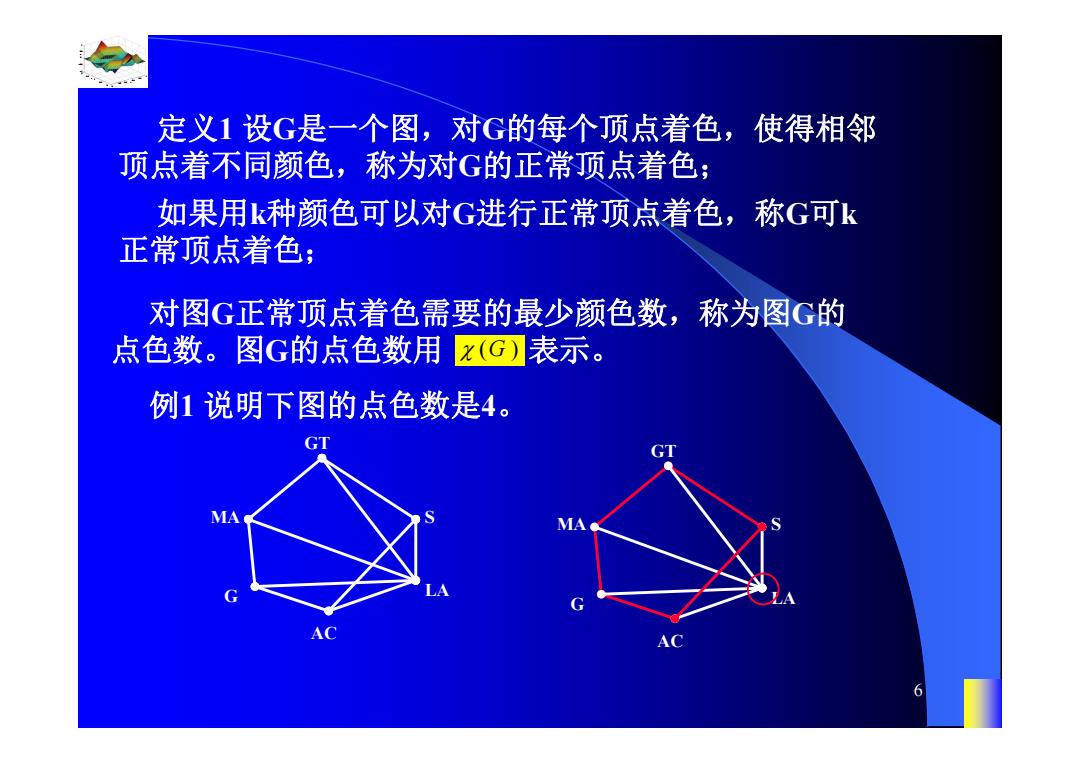
定义1设G是一个图,对G的每个顶点着色,使得相邻 顶点着不同颜色,称为对G的正常顶点着色; 如果用k种颜色可以对G进行正常顶点着色,称G可k 正常顶点着色; 对图G正常顶点着色需要的最少颜色数,称为图G的 点色数。图G的点色数用 x(G)表示。 例1说明下图的点色数是4。 GT GT AC 6
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义1 设G是一个图,对G的每个顶点着色,使得相邻 顶点着不同颜色,称为对G的正常顶点着色; 如果用k种颜色可以对G进行正常顶点着色,称G可k 正常顶点着色; 对图G正常顶点着色需要的最少颜色数,称为图G的 点色数。图G的点色数用 表示。 ( ) G 例1 说明下图的点色数是4。 GT MA G AC LA S GT MA G AC LA S