
本次课主要内容 匈牙利算法与最优匹配算法 (一)、匈牙利算法 (二)、最优匹配算法
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、匈牙利算法 (二)、最优匹配算法 匈牙利算法与最优匹配算法

(一)、 匈牙利算法 1、偶图中寻找完美匹配 (1)、问题 设G=X,Y),X=Y,在G中求一完美匹配M. (2)、基本思想 从任一初始匹配M出发,通过寻求一条M,可扩路P,令 M=M,△EP),得到比M,更大的匹配M(近似于迭代思想)。 (3)、M可扩路寻找方法-交错树方法 1965年,Edmonds首先提出:用扎根于M非饱和点u的M 交错树的生长来求M可扩路
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 (一)、匈牙利算法 1、偶图中寻找完美匹配 (1) 、问题 设G=(X, Y), |X|=|Y|, 在G中求一完美匹配M. (2) 、基本思想 从任一初始匹配M0出发,通过寻求一条M0可扩路P,令 M1=M0ΔE(P), 得到比M0更大的匹配M1(近似于迭代思想)。 (3) 、M可扩路寻找方法---交错树方法 1965年,Edmonds首先提出: 用扎根于M非饱和点u的M 交错树的生长来求M可扩路
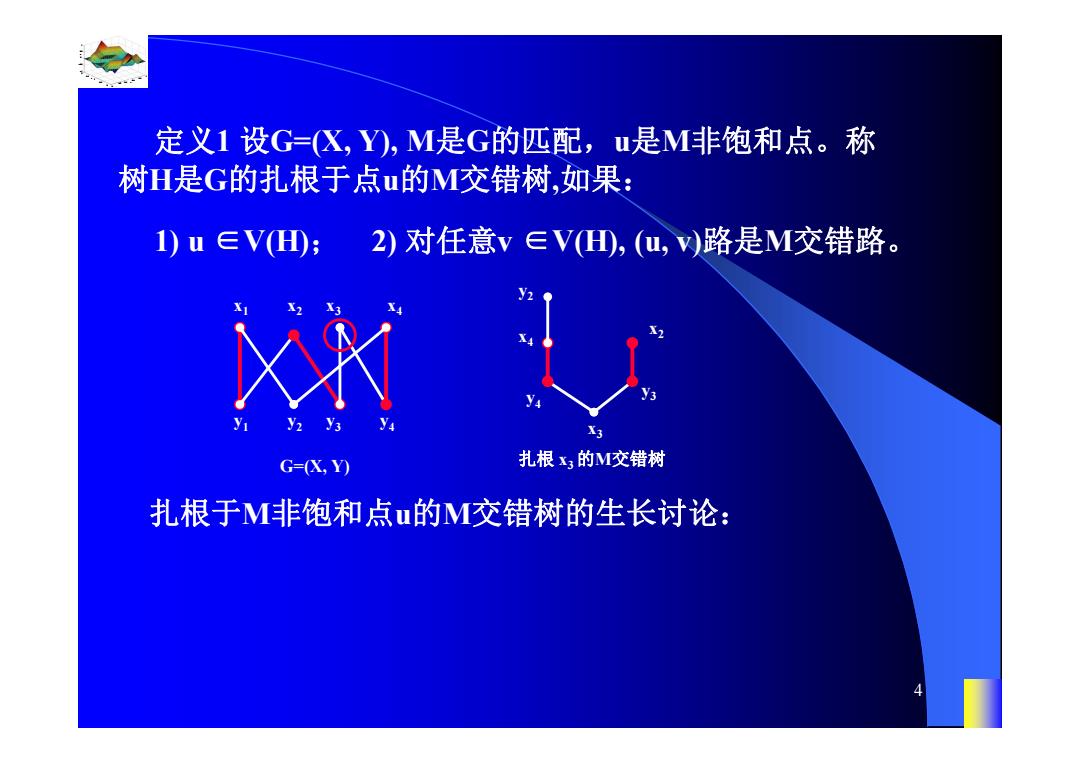
定义1设G=X,Y),M是G的匹配,u是M非饱和点。称 树H是G的扎根于点u的M交错树,如果: 1)u∈V;2)对任意v∈V,(u,v)路是M交错路。 G=(X,Y) 扎根x3的M交错树 扎根于M非饱和点u的M交错树的生长讨论:
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 定义1 设G=(X, Y), M是G的匹配,u是M非饱和点。称 树H是G的扎根于点u的M交错树,如果: 1) u ∈V(H); 2) 对任意v ∈V(H), (u, v)路是M交错路。 x1 x2 x3 x4 y1 y2 y3 y4 G=(X, Y) x3 x x2 4 y4 y3 y2 扎根 x3 的M交错树 扎根于M非饱和点u的M交错树的生长讨论:
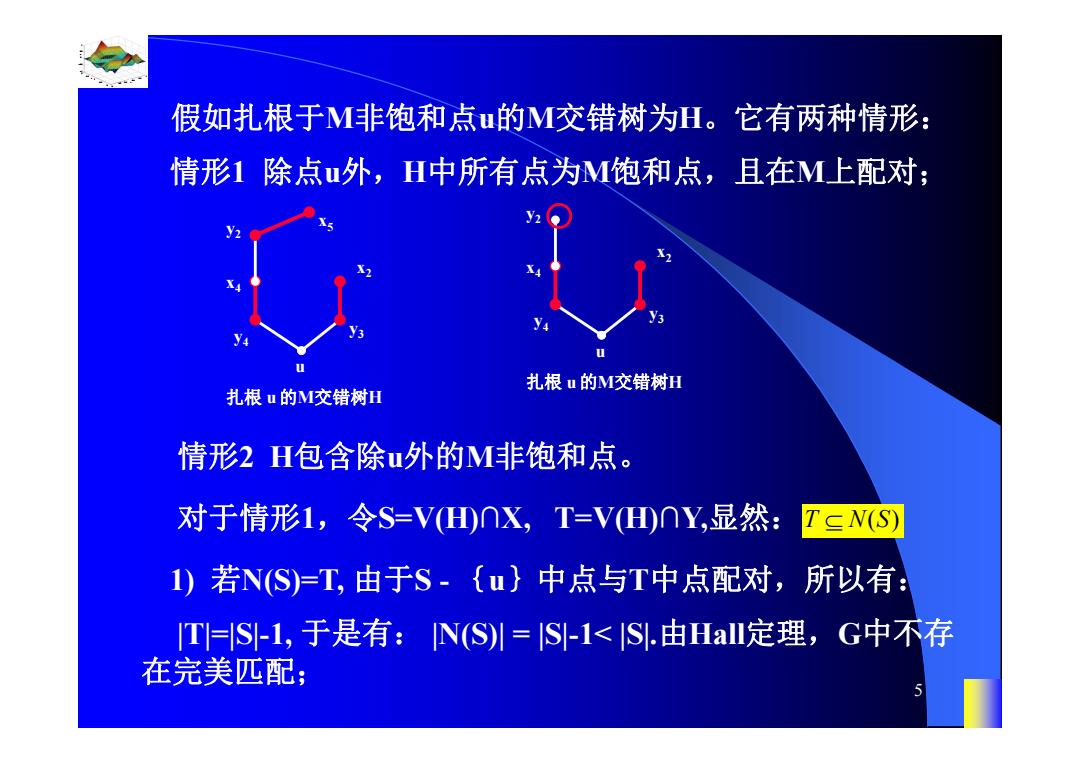
假如扎根于M非饱和点u的M交错树为H。它有两种情形: 情形1除点u外,H中所有点为M饱和点,且在M上配对; 扎根u的M交错树H 扎根u的M交错树H 情形2H包含除u外的M非饱和点。 对于情形1,令S=VH山∩X,T=V山∩Y,显然: TCN(S) 1)若NS)=T,由于S-{u}中点与T中点配对,所以有: IT=S-1,于是有:N(S川=IS-1<IS.由Hal定理,G中不存 在完美匹配
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 假如扎根于M非饱和点u的M交错树为H。它有两种情形: 情形1 除点u外,H中所有点为M饱和点,且在M上配对; x4 u x2 y4 y3 y2 扎根 u 的M交错树H x5 情形2 H包含除u外的M非饱和点。 x4 u x2 y4 y3 y2 扎根 u 的M交错树H 对于情形1,令S=V(H)∩X, T=V(H)∩Y,显然:T NS ( ) 1) 若N(S)=T, 由于S - {u}中点与T中点配对,所以有: |T|=|S|-1, 于是有: |N(S)| = |S|-1< |S|.由Hall定理,G中不存 在完美匹配;
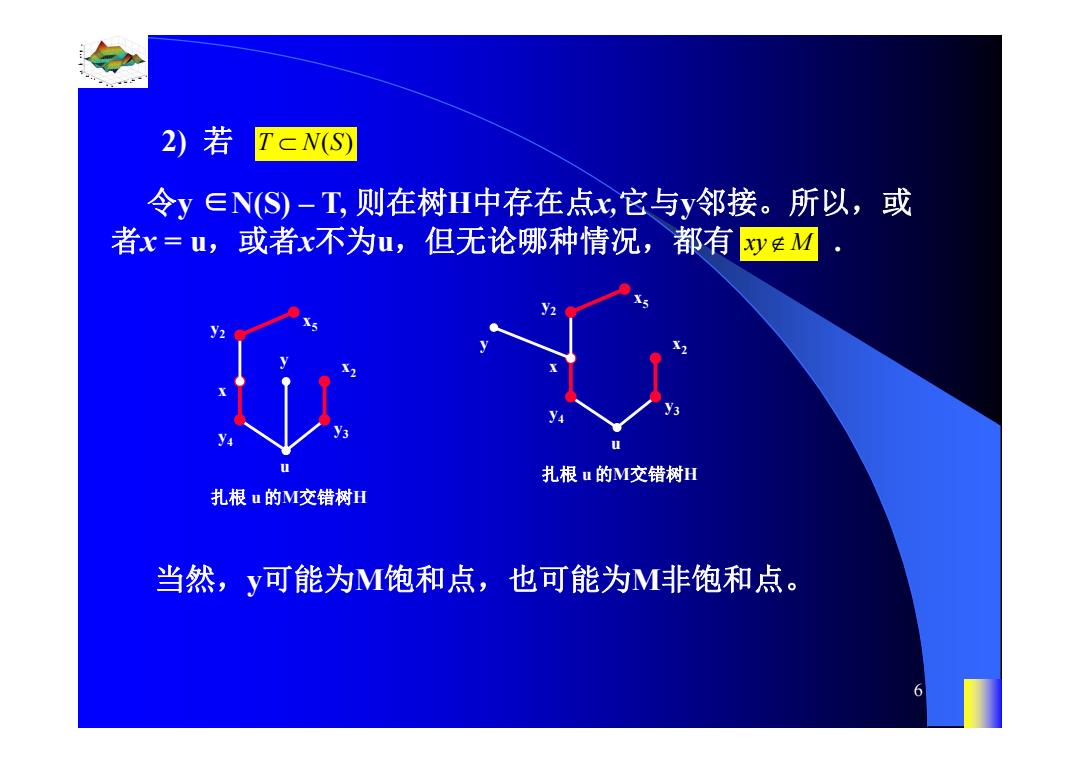
2)若 TCN(S) 令y∈N(S)-T,则在树H中存在点x,它与y邻接。所以,或 者x=u,或者x不为u,但无论哪种情况,都有yEM 扎根u的M交错树H 扎根u的M交错树H 当然,y可能为M饱和点,也可能为M非饱和点
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 2) 若 T NS ( ) 令y ∈N(S) – T, 则在树H中存在点x,它与y邻接。所以,或 者x = u,或者x不为u,但无论哪种情况,都有 xyM . x u x2 y4 y3 y2 扎根 u 的M交错树H x5 y x u x2 y4 y3 y2 扎根 u 的M交错树H x5 y 当然,y可能为M饱和点,也可能为M非饱和点