
本次课主要内容 欧拉图与中国邮路问题 (一)、欧拉图及其性质 (二)、Fleury算法 (三)、中国邮路问题
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 本次课主要内容 (一)、欧拉图及其性质 (二)、Fleury算法 (三)、中国邮路问题 欧拉图与中国邮路问题
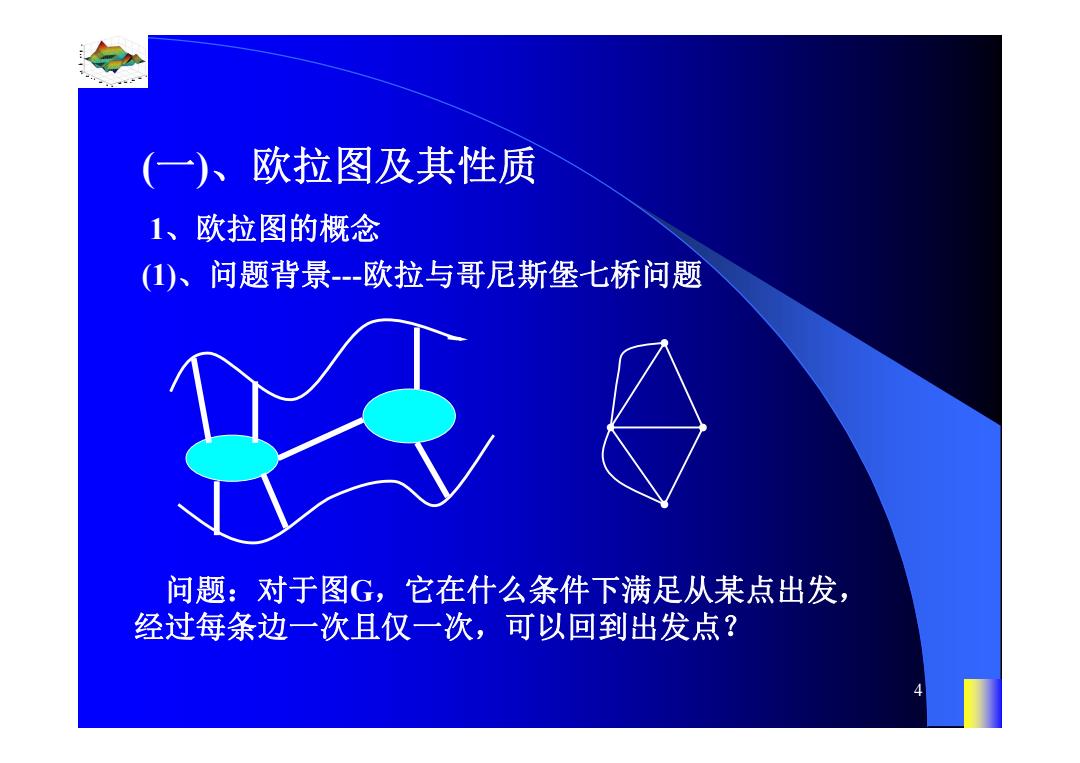
(一)、欧拉图及其性质 1、欧拉图的概念 (1)、问题背景-欧拉与哥尼斯堡七桥问题 问题:对于图G,它在什么条件下满足从某点出发, 经过每条边一次且仅一次,可以回到出发点?
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 1、欧拉图的概念 (一)、欧拉图及其性质 (1)、问题背景---欧拉与哥尼斯堡七桥问题 问题:对于图G,它在什么条件下满足从某点出发, 经过每条边一次且仅一次,可以回到出发点?

哥尼斯堡城(位于德国北部),在欧拉的生活与图论历 史中扮演着非常重要角色。因为它,产生了著名的欧拉 图定理,因为它,产生了图论。 注:一笔画--一中国古老的民间游戏 要求:对于一个图G,笔不离纸,一笔画成。 (2)、欧拉图概念 定义1对于连通图G,如果G中存在经过每条边的闭 迹,则称G为欧拉图,简称G为E图。欧拉闭迹又称为 欧拉环游,或欧拉回路。 3 欧拉图 非欧拉图 非欧拉图 有欧拉迹 无欧拉迹
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 哥尼斯堡城(位于德国北部), 在欧拉的生活与图论历 史中扮演着非常重要角色。因为它,产生了著名的欧拉 图定理,因为它,产生了图论。 注:一笔画----中国古老的民间游戏 要求:对于一个图G, 笔不离纸, 一笔画成. (2)、欧拉图概念 定义1 对于连通图G,如果G中存在经过每条边的闭 迹,则称G为欧拉图,简称G为E图。欧拉闭迹又称为 欧拉环游,或欧拉回路。 欧拉图 4 1 3 2 4 1 3 2 非欧拉图 有欧拉迹 非欧拉图 无欧拉迹 1 2 3 4

2、欧拉图的性质 定理1下列陈述对于非平凡连通图G是等价的: 1)G是欧拉图; (2)G的顶点度数为偶数; (3)G的边集合能划分为圈。 证明:(1)→(2) 由(1),设C是欧拉图G的任一欧拉环游,v是G中任 意顶点,v在环游中每出现一次,意味在G中有两条不 同边与v关联,所以,在G中与v关联的边数为偶数,即 v的度数为偶数,由v的任意性,即证明(2)。 (2)→(3) 由于G是连通非平凡的且每个顶点度数为偶数,所以 G中至少存在圈C,从G中去掉C,中的边,得到G的生成
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 2、欧拉图的性质 定理1 下列陈述对于非平凡连通图G是等价的: (1) G是欧拉图; (2) G的顶点度数为偶数; (3) G的边集合能划分为圈。 证明: (1)→(2) 由(1),设 C是欧拉图G的任一欧拉环游,v是G中任 意顶点,v在环游中每出现一次,意味在G中有两条不 同边与v关联,所以,在G中与v关联的边数为偶数,即 v的度数为偶数,由v的任意性,即证明(2)。 (2)→(3) 由于G是连通非平凡的且每个顶点度数为偶数,所以 G中至少存在圈C1,从G中去掉C1中的边,得到G的生成

子图G,若G,没有边,则3)成立。否则,G的每个非平 凡分支是度数为偶数的连通图,于是又可以抽取一个圈。 反复这样抽取,E(G)最终划分为若干圈。 (3)→(1) 设C,是G的边划分中的一个圈。若G仅由此圈组成, 则G显然是欧拉图。 否则,由于G连通,所以,必然存在圈C2,它和C有 公共顶点。于是,CUC2是一条含有C与C2的边的欧拉 闭迹,如此拼接下去, 得到包含G的所有边的一条欧拉 闭迹。即证G是欧拉图。 推论1连通图G是欧拉图当且仅当G的顶点度数为偶。 推论2连通非欧拉图G存在欧拉迹当且仅当G中只有两 个顶点度数为奇数
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 子图G1,若G1没有边,则(3)成立。否则,G1的每个非平 凡分支是度数为偶数的连通图,于是又可以抽取一个圈。 反复这样抽取,E(G)最终划分为若干圈。 (3)→(1) 设C1是G的边划分中的一个圈。若G仅由此圈组成, 则G显然是欧拉图。 否则,由于G连通,所以,必然存在圈C2,它和C1有 公共顶点。于是,C1∪C2是一条含有C1与C2的边的欧拉 闭迹,如此拼接下去,得到包含G的所有边的一条欧拉 闭迹。即证G是欧拉图。 推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。 推论2 连通非欧拉图G存在欧拉迹当且仅当G中只有两 个顶点度数为奇数