
本次课主要内容 哈密尔顿图 (一)、哈密尔顿图的概念 (二)、性质与判定
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、哈密尔顿图的概念 (二)、性质与判定 哈密尔顿图

(一)、哈密尔顿图的概念 1、背景 l857年,哈密尔顿发明了一个游戏cosian Game), 它是由一个木制的正十二面体构成,在它的每个棱角 处标有当时很有名的城市。游戏目的是“环球旅行 ” 为了容易记住被旅游过的城市,在每个棱角上放上 个钉子,再用一根线绕在那些旅游过的城市上(钉子) 由此可以获得旅程的直观表示。 十二面体
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、背景 (一)、哈密尔顿图的概念 1857年, 哈密尔顿发明了一个游戏(Icosian Game). 它是由一个木制的正十二面体构成,在它的每个棱角 处标有当时很有名的城市。游戏目的是“环球旅行”。 为了容易记住被旅游过的城市 ,在每个棱角上放上一 个钉子,再用一根线绕在那些旅游过的城市上(钉子), 由此可以获得旅程的直观表示。 十二面体

哈密尔顿把该游戏以25英镑的价格买给了J.Jacques and Sons公司(该公司如今以制造国际象棋设备而著 名),1859年获得专利权。但商业运作失败了。 该游戏促使人们思考点线连接的图的结构特征。这 就是图论历史上著名的哈密尔顿问题。 哈密尔顿(1805--1865,爱尔兰数学家。个人生活很 不幸,但兴趣广泛:诗歌、光学、天文学和数学无所 不能。他的主要贡献是在代数领域,发现了四元数(第 一个非交换代数),他认为数学是最美丽的花朵。 2、哈密尔顿图与哈密尔顿路 定义1如果经过图G的每个顶点恰好一次后能够回到 出发点,称这样的图为哈密尔顿图,简称H图。所经过 的闭途径是G的一个生成圈,称为G的哈密尔顿圈
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 哈密尔顿(1805---1865),爱尔兰数学家。个人生活很 不幸,但兴趣广泛:诗歌、光学、天文学和数学无所 不能。他的主要贡献是在代数领域,发现了四元数(第 一个非交换代数),他认为数学是最美丽的花朵。 哈密尔顿把该游戏以25英镑的价格买给了J.Jacques and Sons公司 (该公司如今以制造国际象棋设备而著 名) ,1859年获得专利权。但商业运作失败了。 该游戏促使人们思考点线连接的图的结构特征。这 就是图论历史上著名的哈密尔顿问题。 2、哈密尔顿图与哈密尔顿路 定义1 如果经过图G的每个顶点恰好一次后能够回到 出发点,称这样的图为哈密尔顿图,简称H图。所经过 的闭途径是G的一个生成圈,称为G的哈密尔顿圈
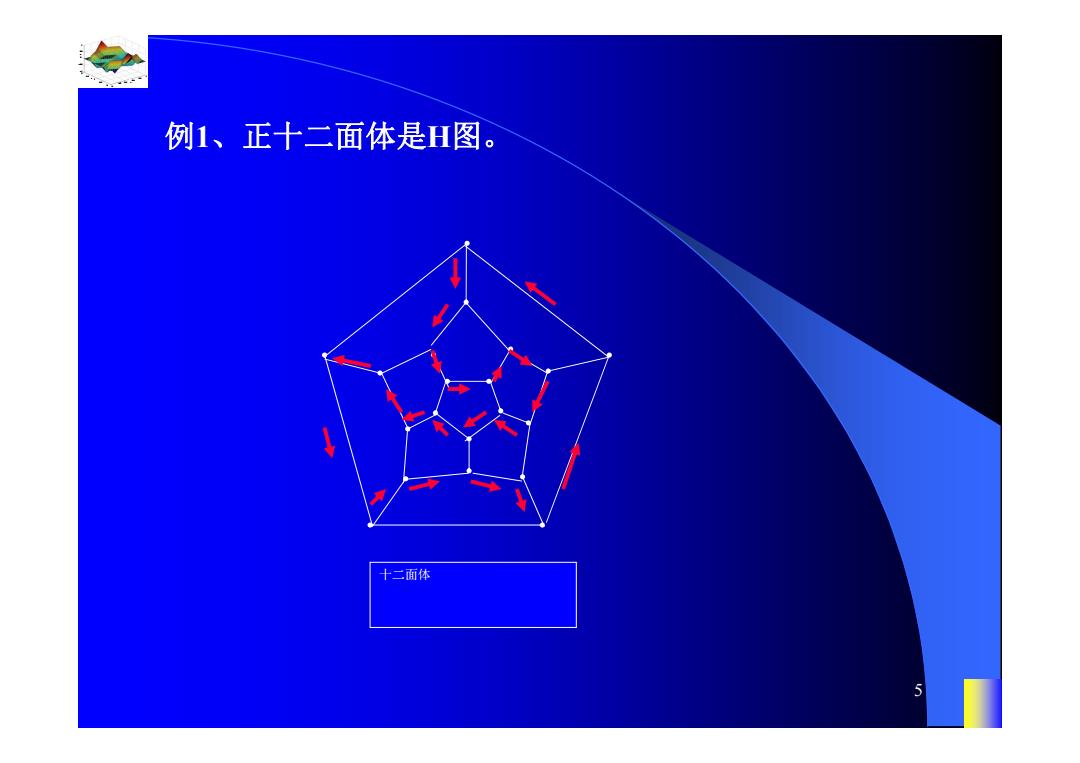
例1、正十二面体是H图。 十二面体
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 例1、正十二面体是H图。 十二面体
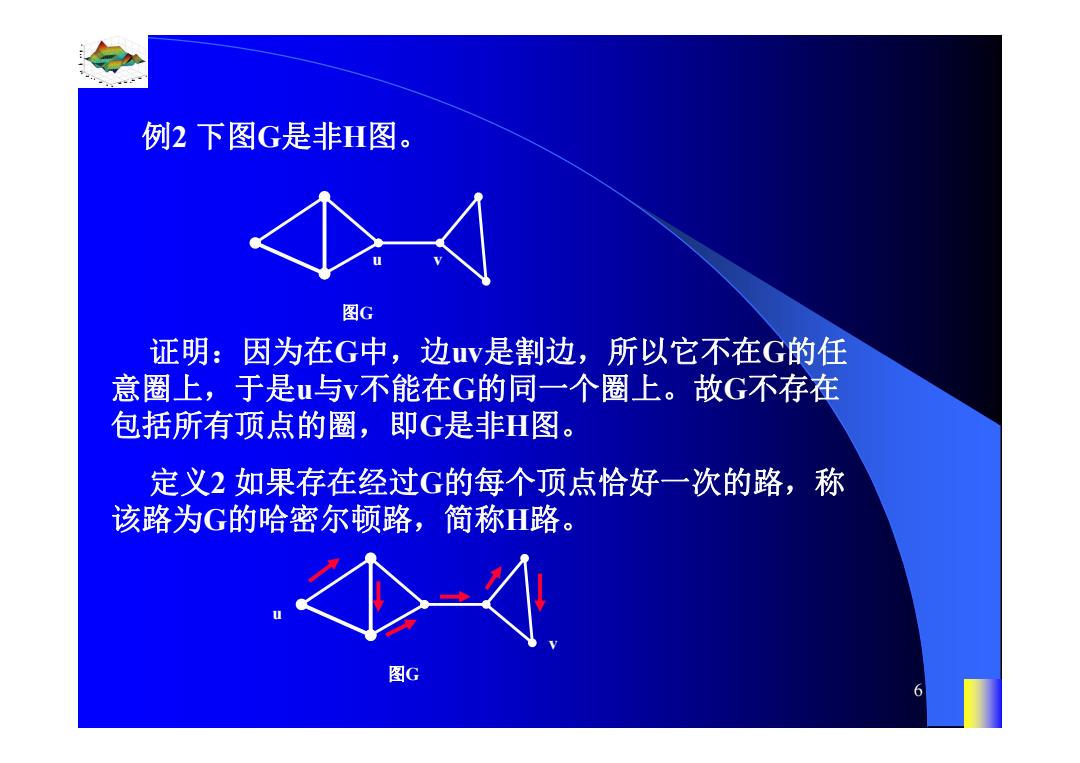
例2下图G是非H图。 图G 证明:因为在G中,边v是割边,所以它不在G的任 意圈上,于是u与v不能在G的同一个圈上。故G不存在 包括所有顶点的圈,即G是非H图。 定义2如果存在经过G的每个顶点恰好一次的路,称 该路为G的哈密尔顿路,简称H路。 图G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 例2 下图G是非H图。 证明:因为在G中,边uv是割边,所以它不在G的任 意圈上,于是u与v不能在G的同一个圈上。故G不存在 包括所有顶点的圈,即G是非H图。 图G u v 定义2 如果存在经过G的每个顶点恰好一次的路,称 该路为G的哈密尔顿路,简称H路。 u v 图G