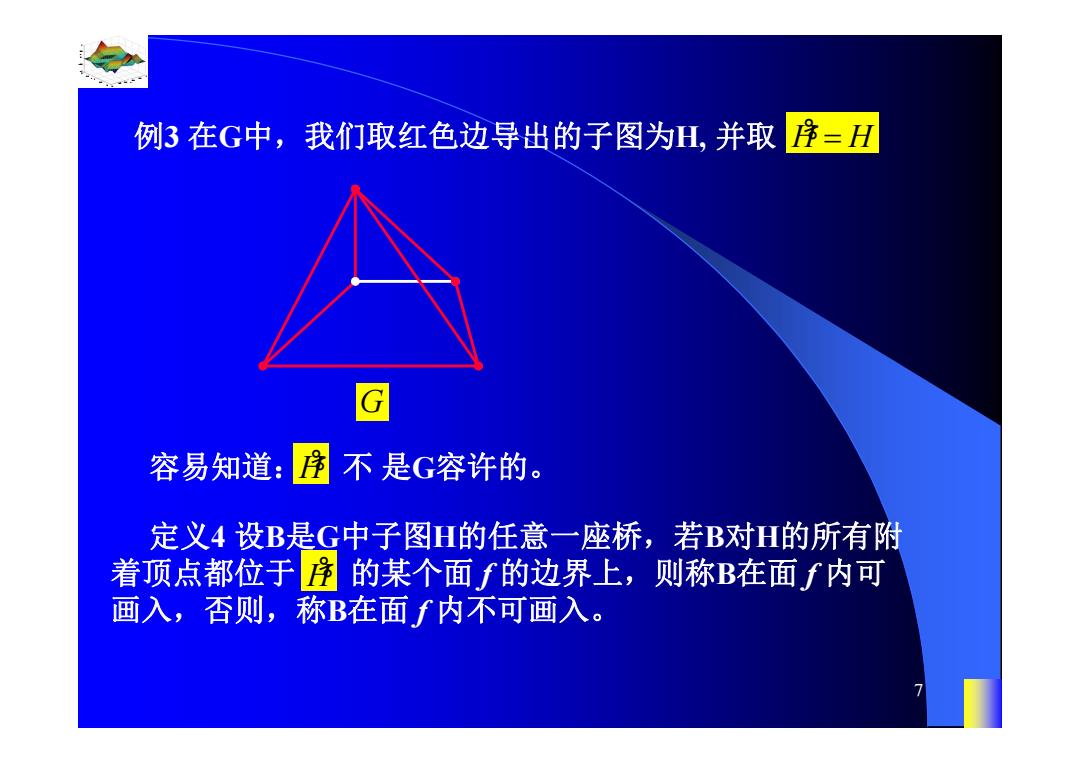
例3在G中,我们取红色边导出的子图为H,并取 序=H G 容易知道:序不是G容许的。 定义4设B是G中子图H的任意一座桥,若B对H的所有附 着顶点都位于序的某个面f的边界上,则称在面f内可 画入,否则,称B在面f内不可画入
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 例3 在G中,我们取红色边导出的子图为H, 并取 H% H 容易知道: 不 是G容许的。 G H% 定义4 设B是G中子图H的任意一座桥,若B对H的所有附 着顶点都位于 的某个面 f 的边界上,则称B在面 f 内可 画入,否则,称B在面 f 内不可画入。 H%
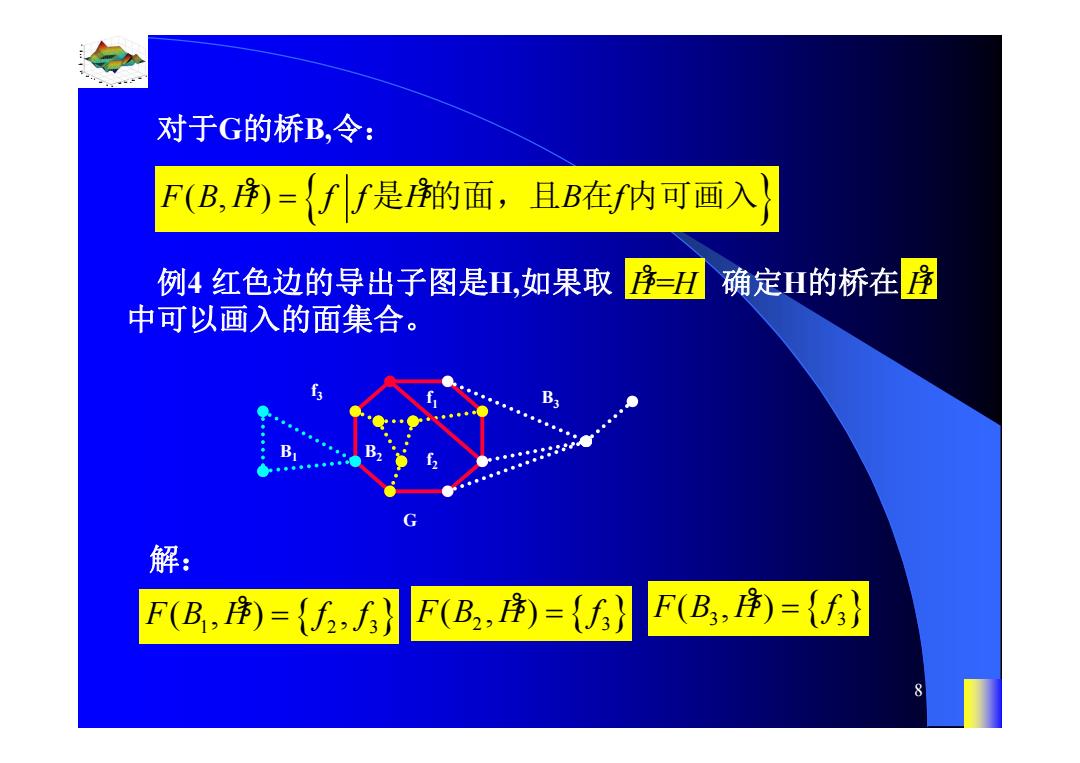
对于G的桥B,令: F(B,)={//是的面,且B在内可画入》 例4红色边的导出子图是H,如果取序=H 确定H的桥在序 中可以画入的面集合。 G 解: F(B,序={,} F(B2,净)={f} F(B,={f} 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 对于G的桥B,令: 例4 红色边的导出子图是H,如果取 确定H的桥在 中可以画入的面集合。 FBH f f H B f (, ) % % 是 的面,且 在 内可画入 H%=H H% B3 B1 B2 f3 f2 f1 G F(,) , BH f f 1 23 % 解: F(,) BH f 2 3 % F(,) BH f 3 3 %

定理1设序 是G容许的,则对于H的每座桥B: F(B,序)≠Φ 证明:因序是G容许的,由定义,存在G的一个平面嵌 入ě,使得: 序 于是,H的桥B所对应的帝 的子图,必然限制在序的 某个面内。所以: F(B,序)≠Φ 注:定理1实际上给出了一个图是可平面图的一个必要条 件。这个必要条件表明:如果存在G的一个可平面子图H
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 定理1 设 是 H% G容许的,则对于H的每座桥B: FBH (, ) % 证明:因 是G容许的,由定义,存在G的一个平面嵌 入 ,使得: H% G% H% G% 于是,H的桥B所对应的 的子图,必然限制在 的 某个面内。所以: G% H% FBH (, ) % 注:定理1实际上给出了一个图是可平面图的一个必要条 件。这个必要条件表明:如果存在G的一个可平面子图H