
本次课主要内容 网络的容错性参数 (一)、连通度的概念与性质 (二)、描述连通性的其它参数简介(内容拓展
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、连通度的概念与性质 (二)、描述连通性的其它参数简介(内容拓展) 网络的容错性参数

(一)、连通度的概念与性质 1、点连通度与边连通度的概念 定义1给定连通图G,设V©,若GV不连通, 称V为G的一个点割集,含有k个顶点的点割集 称为k顶点割。G中点数最少的顶点割称为最小顶点割。 例如: G2 在G中:{y3},,{v5,V3),{vs,V4}等是点割集。 在G,中没有点割集
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 1、点连通度与边连通度的概念 定义1 给定连通图G,设 ,若G -V' 不连通, 称V'为G的一个点割集,含有k个顶点的点割集 称为k顶点割。G中点数最少的顶点割称为最小顶点割。 例如: (一)、连通度的概念与性质 V VG ( ) G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 在G1中:{v3}, {v5, v3}, {v5, v4}等是点割集。 在G2中没有点割集
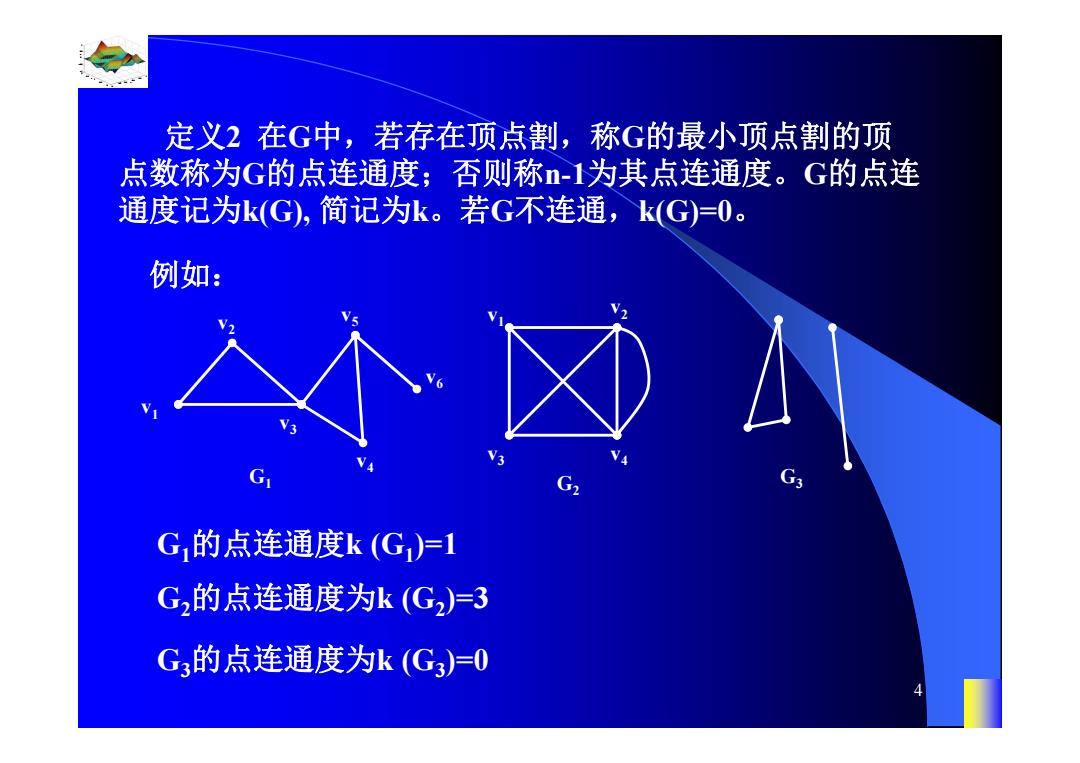
定义2在G中,若存在顶点割,称G的最小顶点割的顶 点数称为G的点连通度;否则称-1为其点连通度。G的点连 通度记为k(G),简记为k。若G不连通,k(G)=0。 例如: G,的点连通度k(G)=1 G,的点连通度为k(G2)=3 G3的点连通度为k(G3)=0
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 定义2 在G中,若存在顶点割,称G的最小顶点割的顶 点数称为G的点连通度;否则称n-1为其点连通度。G的点连 通度记为k(G), 简记为k。若G不连通,k(G)=0。 例如: G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 G1的点连通度k (G1)=1 G2的点连通度为k (G2)=3 G3 G3的点连通度为k (G3)=0
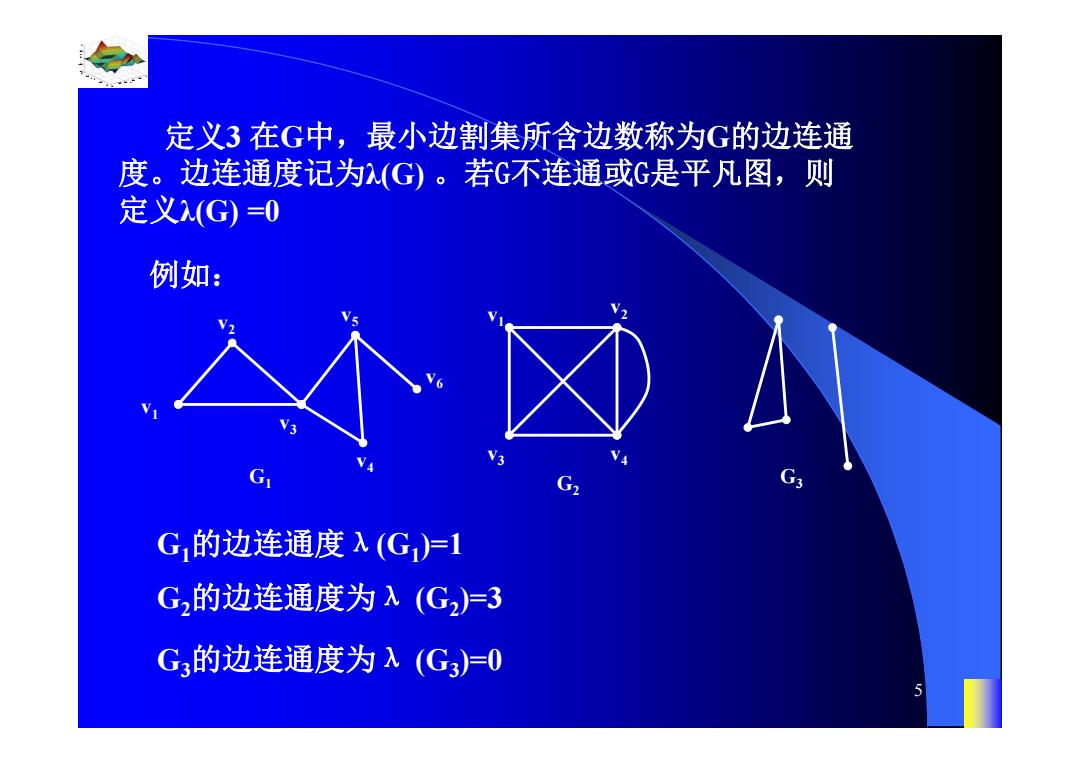
定义3在G中,最小边割集所含边数称为G的边连通 度。边连通度记为(G)。若G不连通或G是平凡图,则 定义(G)=0 例如: G,的边连通度λ(G)=1 G,的边连通度为λ(G,)=3 G的边连通度为入(G3)=0
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义3 在G中,最小边割集所含边数称为G的边连通 度。边连通度记为λ(G) 。若G不连通或G是平凡图,则 定义λ(G) =0 例如: G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 G1的边连通度λ(G1)=1 G2的边连通度为λ (G2)=3 G3 G3的边连通度为λ (G3)=0
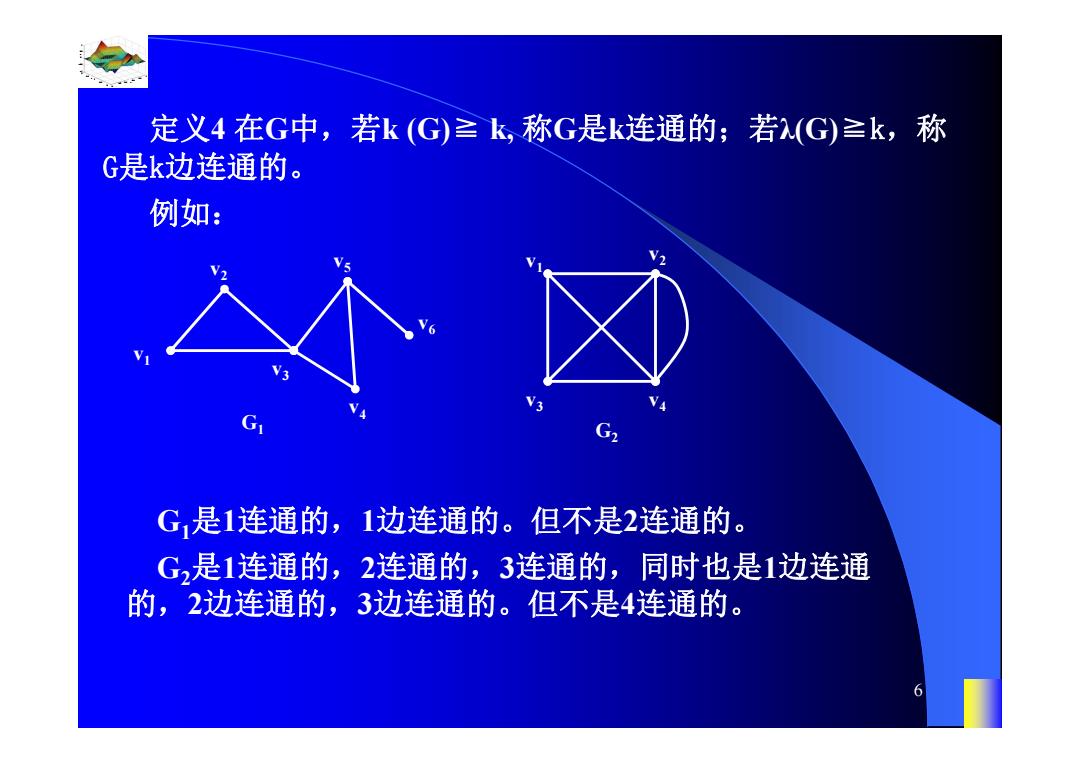
定义4在G中,若k(G)≥k,称G是k连通的;若(G)≥k,称 G是k边连通的。 例如: G,是1连通的,1边连通的。但不是2连通的。 G,是1连通的,2连通的,3连通的,同时也是1边连通 的,2边连通的,3边连通的。但不是4连通的
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义4 在G中,若k (G)≧ k, 称G是k连通的;若λ(G)≧k,称 G是k边连通的。 例如: G1 v5 v4 v3 v2 v1 v6 G2 v3 v4 v v2 1 G1是1连通的,1边连通的。但不是2连通的。 G2是1连通的,2连通的,3连通的,同时也是1边连通 的,2边连通的,3边连通的。但不是4连通的