
§4.1数学期望 定理 。设Y是随机变量X的函数:Y=g(X),其中g是连续函数 ()X是离散型随机变量,分布律为 P{X=Xx}=Pk,k=1,2,. 若级数∑g(xs)p绝对收敛,则有E(Y)=E(g(X)=∑g(xx)p -1 (X是连续型随机变量,概率密度为fx), 若积分g(x)f(x)d绝对收敛,则有 E(Y)=E(g(x))=g(x)f(x)dx 。这样求E(Y)而不必算出Y的分布 17/92
17/92 §4.1 数学期望 定理 ⚫ 设Y是随机变量X的函数:Y=g(X),其中g是连续函数 (i) X是离散型随机变量,分布律为 P{X=xk }=pk,k=1,2,… 若级数 绝对收敛,则有E(Y)=E(g(X))= (ii)X是连续型随机变量,概率密度为f(x), 若积分 绝对收敛,则有 E(Y)=E(g(X))= 这样求E(Y)而不必算出Y的分布 =1 ( ) k k pk g x =1 ( ) k k pk g x − g(x) f (x)dx − g(x) f (x)dx

§4.1数学期望 定理的证明(略),以下对离散型X进行简要说明 00 EY)=∑yP{Y=y} =∑yP{g(X)=y} k=1 k=1 00 三 :∑PX=x》=(∑PX=x》 k=1 xi:g(xi)=yk k=1 xi:g(xi)=yk 0 ∑(∑g(x)PX=x,) k=1 xi:g(xi)=yk ⊙实际上是对所有的X的取值的概率的加权求和 EY)=∑g(x,)PX=x,} t=1 9连续型的特例情况下证明,请参看教材 18/92
18/92 §4.1 数学期望 定理的证明(略),以下对离散型X进行简要说明 E(Y)= = = = = 实际上是对所有的X的取值的概率的加权求和 E(Y) = 连续型的特例情况下证明,请参看教材 = = 1 { } k k k y P Y y = = 1 { ( ) } k k k y P g X y = = = 1 : ( ) ( { }) k x g x y k i i i k y P X x = = = 1 : ( ) ( { }) k x g x y k i i i k y P X x = = = 1 : ( ) ( ( ) { }) k x g x y i i i i k g x P X x = = 1 ( ) { } t g xt P X xt

§4.1数学期望 9 推广:多维随机变量(X1,X2…,Xn)的函数Y=g(X1,X2…,Xm) 也满足以上定理。 例如:若乙=g(X,Y),且g是连续函数,则 9若X,Y)是连续型随机变量,概率密度为xy),那么 E(Z)=E(g(X,Y))=g(x,y)f(x,y)dxdy 只要该积分绝对收敛则存在 9 若(X,Y)是离散型随机变量,分布律P{X=xY=y》=P i=1,2,…那么 EZ=Eg(X,Y)=∑∑g(x,y)P, i=1 i=l 右边级数绝对收敛 19/92
19/92 §4.1 数学期望 推广:多维随机变量(X1 ,X2 ,…,Xn )的函数Y=g(X1 ,X2 ,…,Xn ) 也满足以上定理。 例如:若Z=g(X,Y),且g是连续函数,则 若(X,Y)是连续型随机变量,概率密度为f(x,y),那么 E(Z)=E(g(X,Y))= 只要该积分绝对收敛则存在 若(X,Y)是离散型随机变量,分布律P{X=xi ,Y=yj }=pij, i,j=1,2, …那么 E(Z)=E(g(X,Y))= , 右边级数绝对收敛 − − g(x, y) f (x, y)dxdy = 1 =1 ( , ) j i i j pij g x y

§4.1数学期望 例9:设随机变量(X,Y)的概率密度为 =32x,I/x<,1 0, 其它 求数学期望EY),E(1/XY) ·解此时可以看成是函数z=g(化y)=y 这样E(Z=EY)gx,yfc,y)=nfx,y) 儿2,=34 也可以先求Y的边缘概率密度,再用数学期望定义求解 9 对于第2个问题 E☑=E-寸号kna =2y= 20/92
20/92 §4.1 数学期望 例9:设随机变量(X,Y)的概率密度为 f(x,y)= 求数学期望E(Y),E(1/(XY)) 解 此时可以看成是函数z=g(x,y)=y 这样E(Z)=E(Y)= = = =3/4 也可以先求Y的边缘概率密度,再用数学期望定义求解 对于第2个问题 E(Z)=E(1/(XY))= = =3/5 0, 其它 3/(2 ), 1/ , 1 3 2 x y x y x x − − g(x, y) f (x, y)dxdy − − yf (x, y)dxdy 1 1/ 3 2 x 3 x dydx x y − − f x y dxdy xy ( , ) 1 1 1/ 4 3 2 x 1 x dydx x y
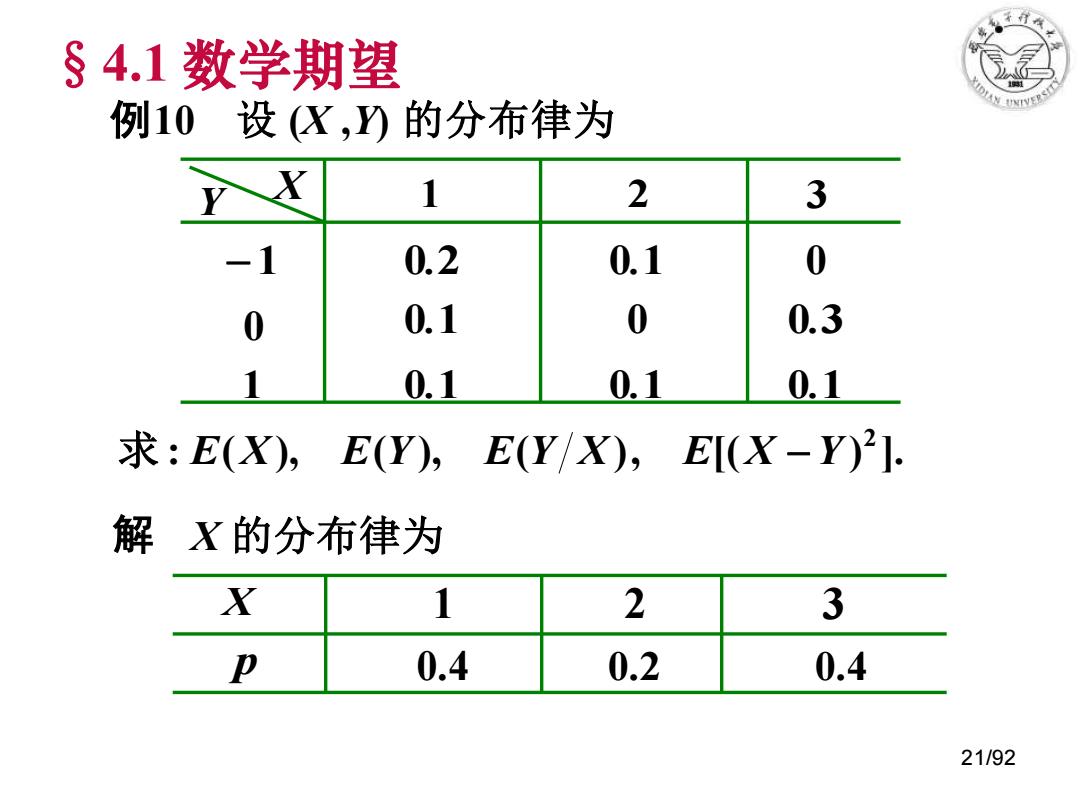
行 §4.1数学期望 例10设(X,)的分布律为 X 1 2 3 0.2 0.1 0 0 0.1 0 0.3 1 0.1 0.1 0.1 求:E(X),E(Y),E(Y/X),E[(X-Y)2] 解X的分布律为 X 1 2 3 0.4 0.2 0.4 21/92
21/92 X p 1 2 3 0.4 0.2 0.4 解 X 的分布律为 X Y 1 2 3 − 1 0 1 0.2 0.1 0.1 0.1 0.1 0.1 0 0 0.3 : ( ), ( ), ( ), [( ) ]. 2 求 E X E Y E Y X E X −Y 例10 设 (X ,Y) 的分布律为 §4.1 数学期望