不相容方程组的示例 。1 如果把第四个方程的右端常数仍取为-9,则其行阶梯变换 的结果为: 1.0000 0 0-1.6757 01.0000 0-1.8378 0 U=rref([A,b])= 0 01.00000.9820 0 0 0 0 1.0000 ·最后一个方程成了一个矛盾方程0=1。这说明方程组不相 容,无解。 ·由此也可以看出,线性方程组求解最好还是用行阶梯简化 的方法。因为它可以给出线性方程组的特征,避免计算的 盲目性
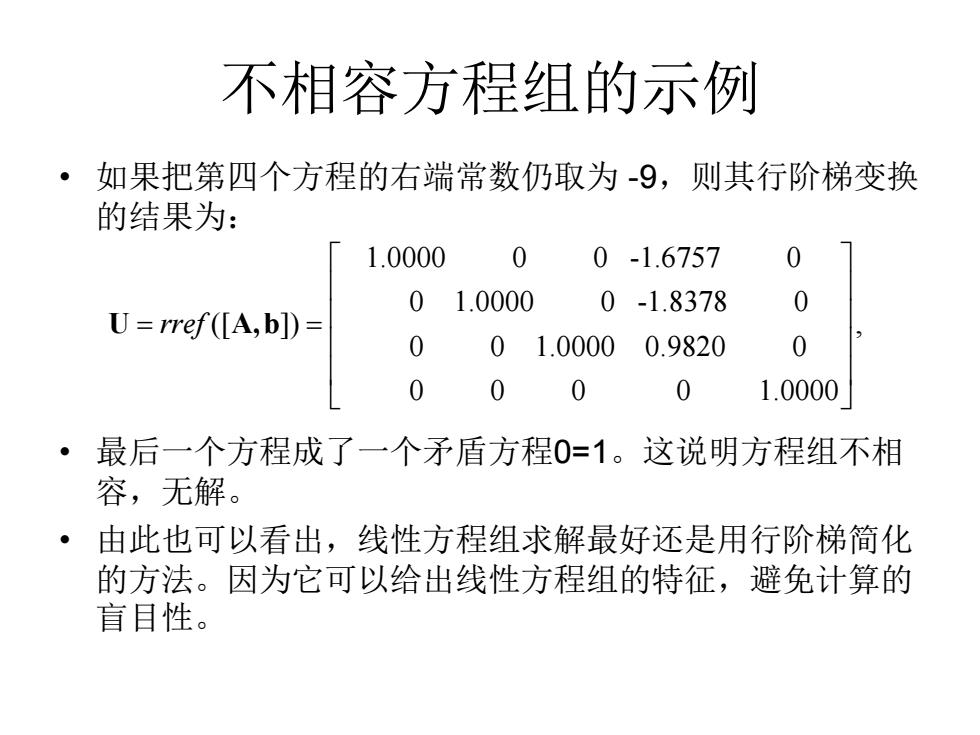
不相容方程组的示例 • 如果把第四个方程的右端常数仍取为 -9,则其行阶梯变换 的结果为: • 最后一个方程成了一个矛盾方程0=1。这说明方程组不相 容,无解。 • 由此也可以看出,线性方程组求解最好还是用行阶梯简化 的方法。因为它可以给出线性方程组的特征,避免计算的 盲目性。 1.0000 0 0 -1.6757 0 0 1.0000 0 -1.8378 0 ([ ]) 0 0 1.0000 0.9820 0 0 0 0 U A,b = = rref , 0 1.0000

【例55-4】多项式插值问题 给出平面上4个点的坐标值如右表, t 2 3 (1)。求对它进行插值的三次多项式, (2)。求t=1.5处f的近似值。 f(t) 3 0 -16 (3)。如果要求此多项式多通过一点(1,5),求其系数。 ·解:用多项式f(t)=a+a,t+at+at 来插值,令它在四点上的值与表中相同,,得到 a=3 100 0 a a+a1+a2+43=0 11 41 0 a+2a1+4a2+843=-1 12 4 8 a。+3a,+6a,+9a=613927 a 6
【例5-5-4】多项式插值问题 给出平面上4个点的坐标值如右表, (1)。求对它进行插值的三次多项式, (2)。求t=1.5处f的近似值。 (3)。如果要求此多项式多通过一点(-1,5),求其系数。 • 解:用多项式 来插值,令它在四点上的值与表中相同,,得到 ti 0 1 2 3 f(ti ) 3 0 -1 6 0 0 0 1 2 3 1 0 1 2 3 2 0 1 2 3 3 3 1 0 0 0 3 0 1 1 1 1 0 , 2 4 8 1 1 2 4 8 1 3 6 9 6 1 3 9 27 6 a a a a a a a a a a a a a a a a a = + + + = = + + + = − − + + + = 2 3 0 1 2 3 f t a a t a t a t ( ) = + + +