
一阶ODE 第六章 常微分方程初步 一阶线性ODE dy+p(x)y=q()的通解为: d y=Cea+eireafg)ersaiax 齐次方程通解 非齐次方程特解 即 y=efr[c+jteodx 注意:求解微分方程时,X,y的地位可互换 1.y-1y=-1 X 2.(2y2+y-x)dy-dr=0 12
12 一阶ODE 第六章 常微分方程初步 的通解为: 齐次方程通解 非齐次方程特解 即 注意: 求解微分方程时, 的地位可互换 . 一阶线性ODE ( )d ( )d ( ) d p x x p x x y e C q x e x

一阶ODE 第六章 常微分方程初步 Bernoul1i方程 形如 dy+p(xy=gxy(n≠0,) d 的一阶微分方程称为Bernoulli方程 当n=0或n=1时,该方程是线性ODE; 当n≠0,n≠1时,该方程不是线性的 解法:方程两边同除y”并令z=y”,化为一阶LODE 例:求方程 dy =xy+xy3 的通解 dx 13
13 一阶ODE 第六章 常微分方程初步 当 时, 该方程不是线性的 . 当 或 时,该方程是线性ODE; 例: 求方程 的通解. Bernoulli方程 形如 的一阶微分方程称为Bernoulli方程 . 解法: 方程两边同除 并令 化为一阶LODE
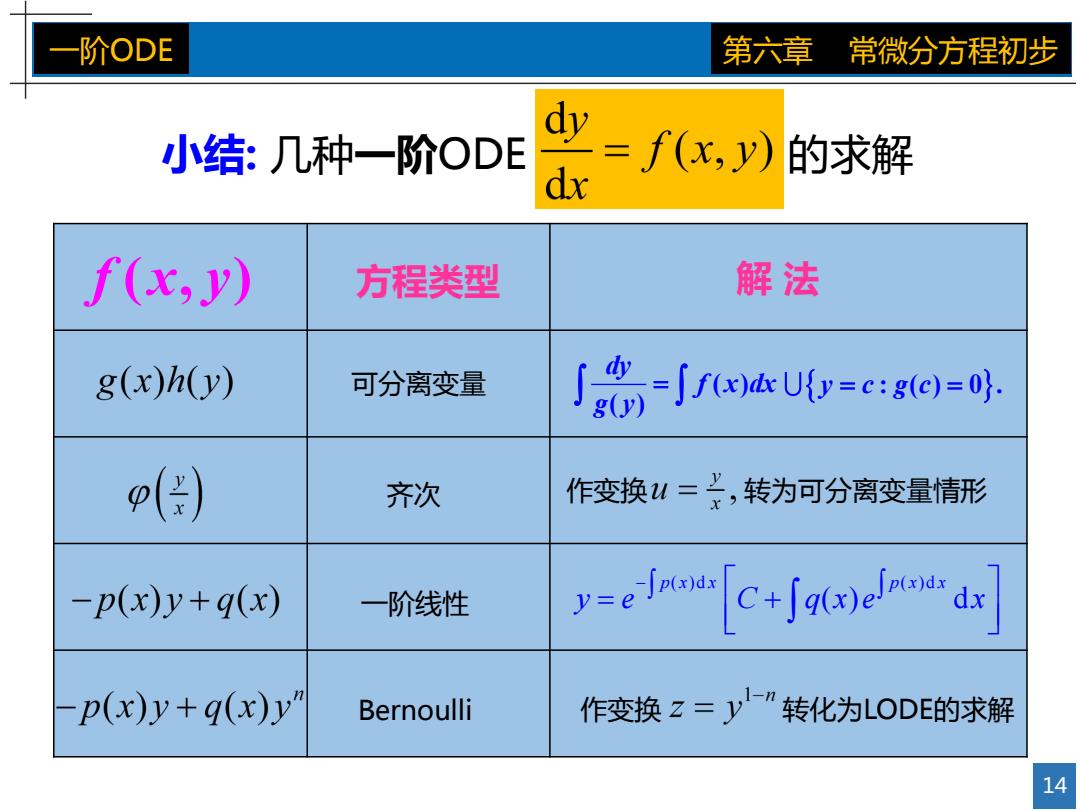
一阶ODE 第六章 常微分方程初步 小结:几种一阶ODE =f(x,)的求解 dx f(c,) 方程类型 解法 g(x)h(y) 可分离变量 J-aUy=cge= p() 齐次 作变换山=士,转为可分离变量情形 -p(x)y+q(x) 一阶线性 y=er[c+jtaedy p(x)y+q(x)y' Bernoulli 作变换z=y"转化为OD的求解 14
14 一阶ODE 第六章 常微分方程初步 小结: 几种一阶ODE 的求解 可分离变量 齐次 一阶线性 Bernoulli 方程类型 解 法 作变换 转化为LODE的求解 作变换 转为可分离变量情形 ( )d ( )d ( ) d p x x p x x y e C q x e x dy f x dx g y ( ) ( ) y c g c : ( ) 0 . f x y ( , )

可降阶的ODE 第六章 常微分方程初步 可降阶的ODE 1.ym=f(x)型ODE的解法 方程两边积分一次,得 ym-=∫f(x)dr+Ci 再积分可得 y(-2)=[[Jf(x)dx+Ci]dx+C2 =[[ff(x)dx ]dx +Cx+C2 依次通过n次积分,可得含n个任意常数的通解. 15
15 可降阶的ODE 第六章 常微分方程初步 方程两边积分一次,得 再积分可得 1. 型ODE的解法 依次通过 n 次积分, 可得含 n 个任意常数的通解 . 可降阶的ODE ( ) ( ) n y f x

可降阶的ODE 第六章 常微分方程初步 2.ODE中不显含y,以二阶为例:f(x,y,y")=0 f(x,y',y)=0p)→f(x,p,p)=0(此时y”=p') 设一阶ODEf(x,p,p)=0有通解p=p(x,C1), 三y=p(x,C)分y=∫p(x,C)d+C 例:求解方程y”+y=4x(x≠0) 16
16 可降阶的ODE 第六章 常微分方程初步 ( ) ( , , ) 0 y p x f x p p 积分 例: 求解方程 2. ODE中不显含 以二阶为例 : f x y y ( , , ) 0 (此时 ) 设一阶ODE 有通解 f x y y ( , , ) 0