
a b b b 例3计算行列式 b a b 。 b D= b b a 。 b b b b a 解:将第2,3.,n列都加到第1列得 a+(n-1)b b b a+(n-1)b a b b D=a+(n-1)b b b a+(n-1)bbb .a
b b b a b b a b b a b b a b b b D = 解:将第2,3,.,n列都加到第1列得 ( ) ( ) ( ) ( ) 1 1 1 1 a n b b b b a n b a b b D a n b b a b a n b b b a + − + − = + − + − 例3计算行列式

1 b b b 1 a b b =[a+(n-1)b] 1 b a . b bb . a 1 b b b 0 a-b 0 0 0 =[a+(n-1b0 0 a-b 0 0 =[a+(n-1)bla-b"时 0 0 0 .a-b
b b a b a b a b b b b b a n b 1 1 1 1 = + ( −1) a b a b a b b b b a n b − − − = + − 0 0 0 0 0 0 0 0 0 0 0 1 ( 1) ( 1) ( ) . −1 = + − − n a n b a b

注意:行列式的每一行的各元素之和相等时常用 此法。 例如下面的行列式 x-m X . X x2-m . 1 D- Xn x-m . l X X2 x.-m 1 .Xn-m 1 0 1 -m 0 x:-m (2x,-m(-m) i=l 1 0 m
x x x m x x m x x m x x D n n n − − − = 1 2 1 2 1 2 此法。 注意:行列式的每一行的各元素之和相等时常用 例如下面的行列式 m m x m n i i − − = − = 1 0 1 0 1 0 0 ( ) 1 1 1 ( )( ) − = = − − n n i xi m m x x m x m x x x x m n n n n i i − − = − = 2 2 2 1 1 1 1 ( )
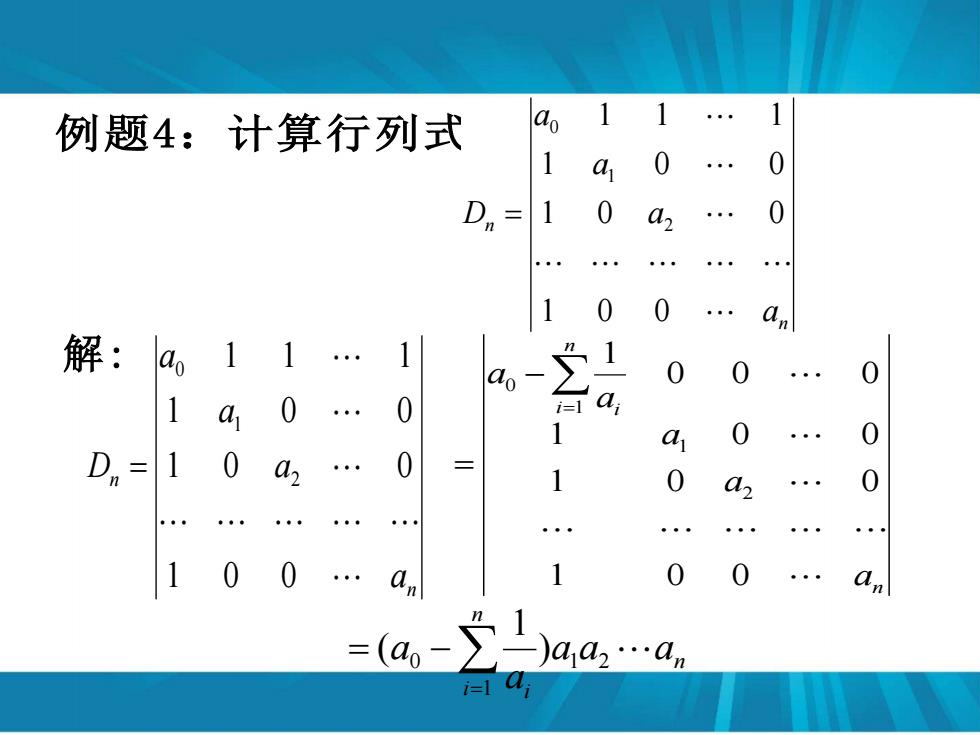
例题4:计算行列式 a 1 1 1 a 0 0 D= 1 0 a, 0 0 解: a11 . 1 ao 0 0 1 41 0 . 0 i=1 1 0 0 D,= 1 0 a 0 1 az 0 1 0 0 . 0 0 an =a,-1a4,a 14
例题4:计算行列式 n n a a a a D 1 0 0 1 0 0 1 0 0 1 1 1 2 1 0 = n n a a a a D 1 0 0 1 0 0 1 0 0 1 1 1 2 1 0 = 解: n n i i a a a a a 1 0 0 1 0 0 1 0 0 0 0 0 1 2 1 1 0 = − = n n i i a a a a a 1 2 1 0 ) 1 ( = = −

2、降阶法 5 3 -1 2 0 1 7 2 5 2 例题5:计算行列式 D= 0 -2 3 1 0 0 -4 -1 4 0 0 2 3 50 53 -12 0 1 7 2 5 2 5 3 -1 2 D- 0 -2 3 1 0 =2(←1)240 -2 3 1 0 -4 -1 4 0 -4 -1 4 0 2 3 5 0 02 3
例题5:计算行列式 0 2 3 5 0 0 4 1 4 0 0 2 3 1 0 1 7 2 5 2 5 3 1 2 0 − − − − D = 0 2 3 5 0 0 4 1 4 0 0 2 3 1 0 1 7 2 5 2 5 3 1 2 0 − − − − D = 0 2 3 5 0 4 1 4 0 2 3 1 5 3 1 2 2 ( 1) 2 5 − − − − = − + 2、降阶法