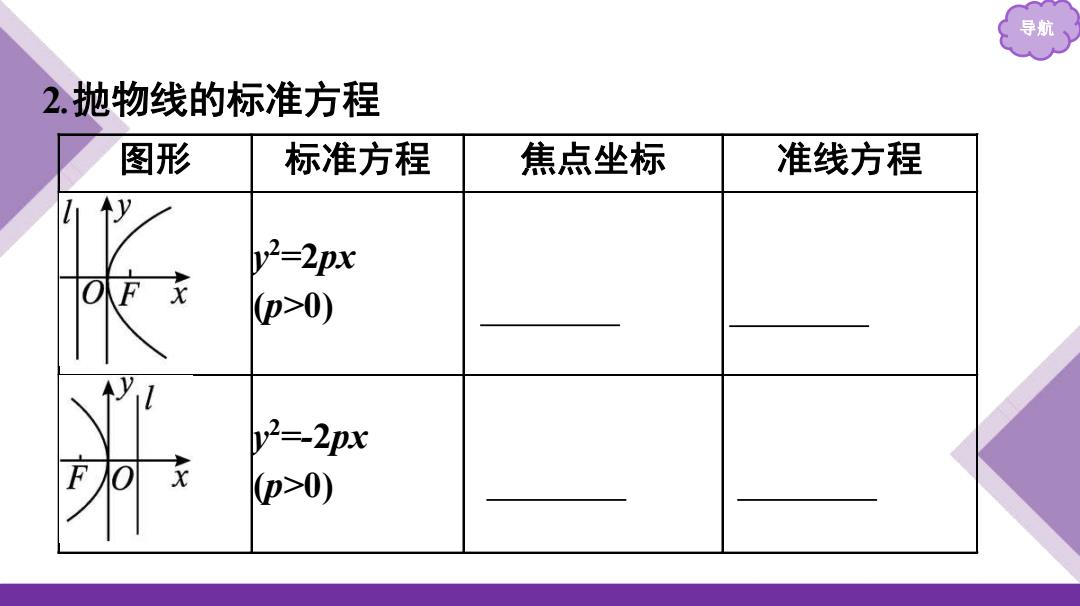
导航 2.抛物线的标准方程 图形 标准方程 焦点坐标 准线方程 y2-2px OF p>0) y2=-2px p>0)
导航 2 .抛物线的标准方程 图形 标准方程 焦点坐标 准线方程 y2=2px (p>0) 𝐩𝟐 ,𝟎 x=-𝐩𝟐 y2=-2px (p>0) - 𝐩𝟐 ,𝟎 x=𝐩𝟐
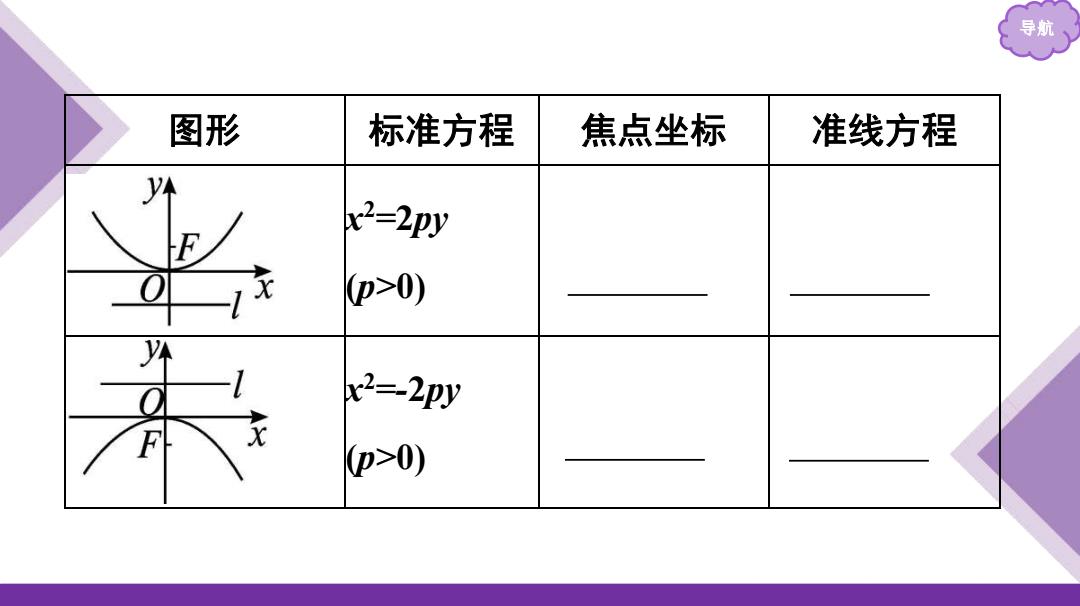
导航 图形 标准方程 焦点坐标 准线方程 x2-2py p>0) x2=-2py p>0)
导航 图形 标准方程 焦点坐标 准线方程 x 2 =2py (p>0) 𝟎, 𝐩 𝟐 y=- 𝐩 𝟐 x 2 =-2py (p>0) 𝟎,- 𝐩 𝟐 y= 𝐩 𝟐

导期 微解读抛物线一定就是二次函数的图象吗? 提示:二次函数的解析式为y=x2+bx+c(吋0),当b,c为0时y=c2 表示焦点在y轴上的地物线,标准方程为x2=二y,当>0时抛物 线开口向上,当<0时,抛物线开口向下.但当抛物线的开口向 左或向右时,方程为y2=±2px(D>0),表示一条曲线,不是二次函 数的图象
导航 微解读 抛物线一定就是二次函数的图象吗? 提示:二次函数的解析式为y=ax2+bx+c(a≠0),当b,c为0时,y=ax2 表示焦点在y轴上的抛物线,标准方程为x 2= y,当a>0时抛物 线开口向上,当a<0时,抛物线开口向下.但当抛物线的开口向 左或向右时,方程为y 2=±2px(p>0),表示一条曲线,不是二次函 数的图象. 𝟏 𝒂

导航 课堂·重难突破 根据抛物线方程求焦点坐标和准线方程 典例剖析 1.求下列抛物线的焦点坐标和准线方程: 1 (1y2=-4x;(2)y=8x2; (3)3y2-4x=0;(4)y2=x(0)
导航 课堂·重难突破 一 根据抛物线方程求焦点坐标和准线方程 典例剖析 1.求下列抛物线的焦点坐标和准线方程: (1)y 2=- x;(2)y=8x 2 ; (3)3y 2 -4x=0;(4)y 2=ax(a≠0). 𝟏 𝟒

导 解:()由方程2-知,抛物线开口向左,焦点在x轴的负半轴 上,2即4号=云所以焦点坐标为(60)准线方程为x 16 ②)抛物线方程化为2日,抛物线开口向上,焦点在y抽的正半 轴上,2p8号=2所以焦点坐标为(0,立)准线方程为 1 32
导航 解:(1)由方程 y 2 =- 𝟏 𝟒 x 知,抛物线开口向左,焦点在 x 轴的负半轴 上,2p= 𝟏 𝟒 , 𝒑 𝟐 = 𝟏 𝟏𝟔 ,所以焦点坐标为 - 𝟏 𝟏𝟔 ,𝟎 ,准线方程为 x= 𝟏 𝟏𝟔 . (2)抛物线方程化为 x 2 = 𝟏 𝟖 y,抛物线开口向上,焦点在 y 轴的正半 轴上,2p= 𝟏 𝟖 , 𝒑 𝟐 = 𝟏 𝟑𝟐 ,所以焦点坐标为 𝟎, 𝟏 𝟑𝟐 ,准线方程为 y=- 𝟏 𝟑𝟐