
第二章环路参数与相位噪声分析 若在环路中采用如图2-3所示的二阶滤波器,即三阶低通滤波器的电阻R3 取为零。那么二阶低通滤波器的传输函数2]: (1+§) 1 ZF.2nd(S) sC,+C2+Cg)(1+s) (2.2) Wp 其中 1 W:-RC C,+C2+Cg=(b+10w, w。=RC,(C2+C) (2.3) 2.1.2根轨迹法 根轨迹法不但可以方便的得到闭环系统的零极点分布,更能够从直观上把握 开环参数与环路稳定性之间的直接联系[1]。简单起见,以采用二阶滤波器的三阶 锁相环为例,阐述基于根轨迹的环路设计方法。 根据环路传输函数式(2.1)和二阶滤波器传输函数式(2.2),可以得到三阶环路 开环传输函数: Ho(S)=K_S+@: s2(S+W,) (2.4) 其中K=IpKvcobl(2TNC)。环路传输函数有一个零点和三个极点。两个极 点在原点,另外的一个极点ω,和零点2都位于左半平面的实轴上。闭环系统传 输函数: HLs)-H图s+u,+Ks+K0 NH(s)NK(s+@z) (2.5) NK(s+w) H.(S)=(s2+2ω.+w)5+ws) (2.6) ?为二阶系统的阻尼因子,w为自然频率。闭环系统和开环系统相比,零点 位置并没有发生变化,极点分布发生变化了。通过解闭环传输函数H(S)可以得 到闭环的零极点,但是纯粹的数学方法并不能给我们带来直观的物理意义。采用 根轨迹法,可以方便的得到闭环系统的零极点分布,更能够从直观上把握开环参 数与环路稳定性之间的直接联系。图2-4中E点w。表示开环非零极点,F点表 7
第二章 环路参数与相位噪声分析 7 若在环路中采用如图 2-3 所示的二阶滤波器,即三阶低通滤波器的电阻 R3 取为零。那么二阶低通滤波器的传输函数[2]: z F,2nd 123 p (1+ ) 1 ( )= ( ) (1 ) s ω Z s sC C C s ω (2.2) 其中 123 zp z 11 11 2 3 1 ( 1) ( ) CCC ω ω b ω RC RC C C (2.3) 2.1.2 根轨迹法 根轨迹法不但可以方便的得到闭环系统的零极点分布,更能够从直观上把握 开环参数与环路稳定性之间的直接联系[1]。简单起见,以采用二阶滤波器的三阶 锁相环为例,阐述基于根轨迹的环路设计方法。 根据环路传输函数式(2.1)和二阶滤波器传输函数式(2.2),可以得到三阶环路 开环传输函数: ' z o 2 p ( ) ( ) s ω Hs K s s ω (2.4) 其中 K’ =IcpKvcob/(2π NC1)。环路传输函数有一个零点和三个极点。两个极 点在原点,另外的一个极点 ωp和零点 ωz 都位于左半平面的实轴上。闭环系统传 输函数: ' o z c 3 2' ' op z ( ) ( ) ( ) 1+ ( ) NH s NK s ω H s Hs s ω s Ks K ω (2.5) ' z c 2 2 n n p3 ( ) ( ) ( 2 )( ) NK s ω H s s ζω ω s ω (2.6) ζ 为二阶系统的阻尼因子,ωn为自然频率。闭环系统和开环系统相比,零点 位置并没有发生变化,极点分布发生变化了。通过解闭环传输函数 Hc(s)可以得 到闭环的零极点,但是纯粹的数学方法并不能给我们带来直观的物理意义。采用 根轨迹法,可以方便的得到闭环系统的零极点分布,更能够从直观上把握开环参 数与环路稳定性之间的直接联系。图 2-4 中 E 点 ωp表示开环非零极点,F 点表

2~2.4GHz分数分频频率综合器设计 示零点,另外两个极点在原点处。随着开环增益K逐渐增大,闭环极点w1、w2 和w3位置随之发生变化,其中w1和w2为一对共轭极点。当?=V2/2时,对 应B和C两点为系统的稳定边界。在B点,若开环增益K减小,则闭环极点进 入不稳定区域。在C点,若开环增益K增大,则闭环极点同样进入不稳定区域。 因此,为了保证较好的稳定性,应该尽量设置开环增益K?在稳定边界的左半部 分。根轨迹法的本质是选择最优的开环增益使得系统具有最佳的稳定性。 为了计算方便,变量w和K'分别对零点w2归一化 W mwz (2.7) X open loop poles √2 closed loop poles 2 unstable stable B region region .0p1 DA 2 0 =1 图2-4根轨迹示意图 K=kw2 (2.8) 其中m和k分别是wn和K的归一系数。 将式(2.7)和(2.8)代入(2.5)和(2.6)可以得到: 2gm2-(42+b)m+23(b+1)=0 (2.9) k=(1-432)m2+2(b+1)m (2.10) 由式(2.9)和(2.10)得到稳定边界处B和C点的开环增益: k=(1-432)m6+23(b+1)me (2.11) k.=(1-432)m6+23(b+1)m。 (2.12) 其中me和mc为式(2.9)的两个根,满足 8
2~2.4 GHz 分数分频频率综合器设计 8 示零点,另外两个极点在原点处。随着开环增益 K’逐渐增大,闭环极点 ωp1、ωp2 和 ωp3位置随之发生变化,其中 ωp1和 ωp2为一对共轭极点。当ζ 2 2时,对 应 B 和 C 两点为系统的稳定边界。在 B 点,若开环增益 K’减小,则闭环极点进 入不稳定区域。在 C 点,若开环增益 K’增大,则闭环极点同样进入不稳定区域。 因此,为了保证较好的稳定性,应该尽量设置开环增益 K’在稳定边界的左半部 分。根轨迹法的本质是选择最优的开环增益使得系统具有最佳的稳定性。 为了计算方便,变量 ωn和 K’分别对零点 ωz 归一化 ωn z mω (2.7) 2 2 ζ 图 2-4 根轨迹示意图 ' 2 K k ωz (2.8) 其中 m 和 k 分别是 ωn和 K’的归一系数。 将式(2.7)和(2.8)代入(2.5)和(2.6)可以得到: 2 2 2 (4 ) 2 ( 1) 0 ζm ζ b m ζ b (2.9) 2 2 k (1 4 ) 2 ( 1) ζ m ζ b m (2.10) 由式(2.9)和(2.10)得到稳定边界处 B 和 C 点的开环增益: 2 2 kBB B =(1 4 ) 2 ( 1) ζ m ζ b m (2.11) 2 2 kCC C =(1 4 ) 2 ( 1) ζ m ζ b m (2.12) 其中 mB和 mC为式(2.9)的两个根,满足

第二章环路参数与相位噪声分析 42+b me mc 23 (2.13) mem。=b+1 (2.14) 最优的开环增益为k阳和kc的几何平均值,有 Kopt =Kgkc (2.15) kt=Vmm.[1-42)2mm。+2(b+1(1-42)(m3+me)+42(b+102](2.16) 将?=√2/2、式(2.13)和(2.14)代入式(2.16),计算得到: kt=(b+1)32 (2.17) 此时开环环路增益: Kt=(b+1)32w2 (2.18) 将式(2.18)代入式(2.4)并令 H(S)= S+Wz K jw.+w,=1 s2(s+wp) (jw)2(jw.+wp) (2.19) 可以得到: (2.20) 将式(2.18)和(2.20)代入式(2.4),得 H,(s)=(b+)2ws+w,/D+1 (2.21) s2(s+V(b+10w.) 至此可以看出,如果开环增益取稳定边界B和C两点的几何平均值,那么 开环传输函数H(S)只和电容比值b和开环环路带宽wc有关。在电容比值和开环 环路带宽确定的情况下,开环传输函数便能够唯一确定了。 由式(2.18)和(2.20),得 K =(b+1)2w2 (2.22) 9
第二章 环路参数与相位噪声分析 9 2 B C 4 2 ζ b m m ζ (2.13) mm b B C 1 (2.14) 最优的开环增益为 kB和 kC的几何平均值,有 opt B C k kk (2.15) 22 2 2 2 opt B C B C B C k mm (1 4 ) 2 ( 1)(1 4 )( ) 4 ( 1) ζ m m ζ b ζ m m ζ b (2.16) 将ζ 2 2、式(2.13)和(2.14)代入式(2.16),计算得到: 3 2 opt k b ( 1) (2.17) 此时开环环路增益: ' 32 2 opt z K b ( 1) ω (2.18) 将式(2.18)代入式(2.4)并令 ' ' z c z o 2 2 p c cp j () 1 ( ) (j ) (j ) s ω ω ω Hs K K s s ω ω ωω (2.19) 可以得到: c z 1 ω ω b (2.20) 将式(2.18)和(2.20)代入式(2.4),得 1/2 2 c o c 2 c 1 ( ) ( 1) ( ( 1) ) s ω b Hs b ω ss b ω (2.21) 至此可以看出,如果开环增益取稳定边界 B 和 C 两点的几何平均值,那么 开环传输函数 Ho(s)只和电容比值 b 和开环环路带宽 ωc 有关。在电容比值和开环 环路带宽确定的情况下,开环传输函数便能够唯一确定了。 由式(2.18)和(2.20),得 ' 1/2 2 cp vco opt z 1 ( 1) 2π IK b K b ω NC (2.22)
2~2.4GHz分数分频频率综合器设计 1 Wc w,=R,C,b+1 (2.23) 计算得到二阶滤波器的环路参数: lcpKvco b C,=2mNb+1w号 (2.24) C2+C3 -ClKvco 1 =b2TN√b+1w (2.25) 2TTN (b+1)w. R,= lcpKvco b (2.26) 2.1.3相位裕度最大法 相位裕度最大法从开环传输函数的波特图出发,研究环路稳定性和环路参数 之间的关系[2]。开环传输函数Ho(s)在原点处有两个极点,增益以40dB/Dec下 降,之后遇到左半平面的零点,因而增益开始以20dB/Dec下降。再经过开环 环路带宽之外的极点后,增益继续以40dB/Dec下降。若为三阶滤波器,则在 环路带宽之外有两个极点,因而遇到第二个非零极点后,以60dB/Dec下降, 用来抑制DSM调制器引入的量化噪声。下面以二阶滤波器为例,说明相位裕度 最大法求解环路参数的设计流程。 0 中m 0 Wz Wc Wp 图2-5三阶环路开环传输函数的波特图 10
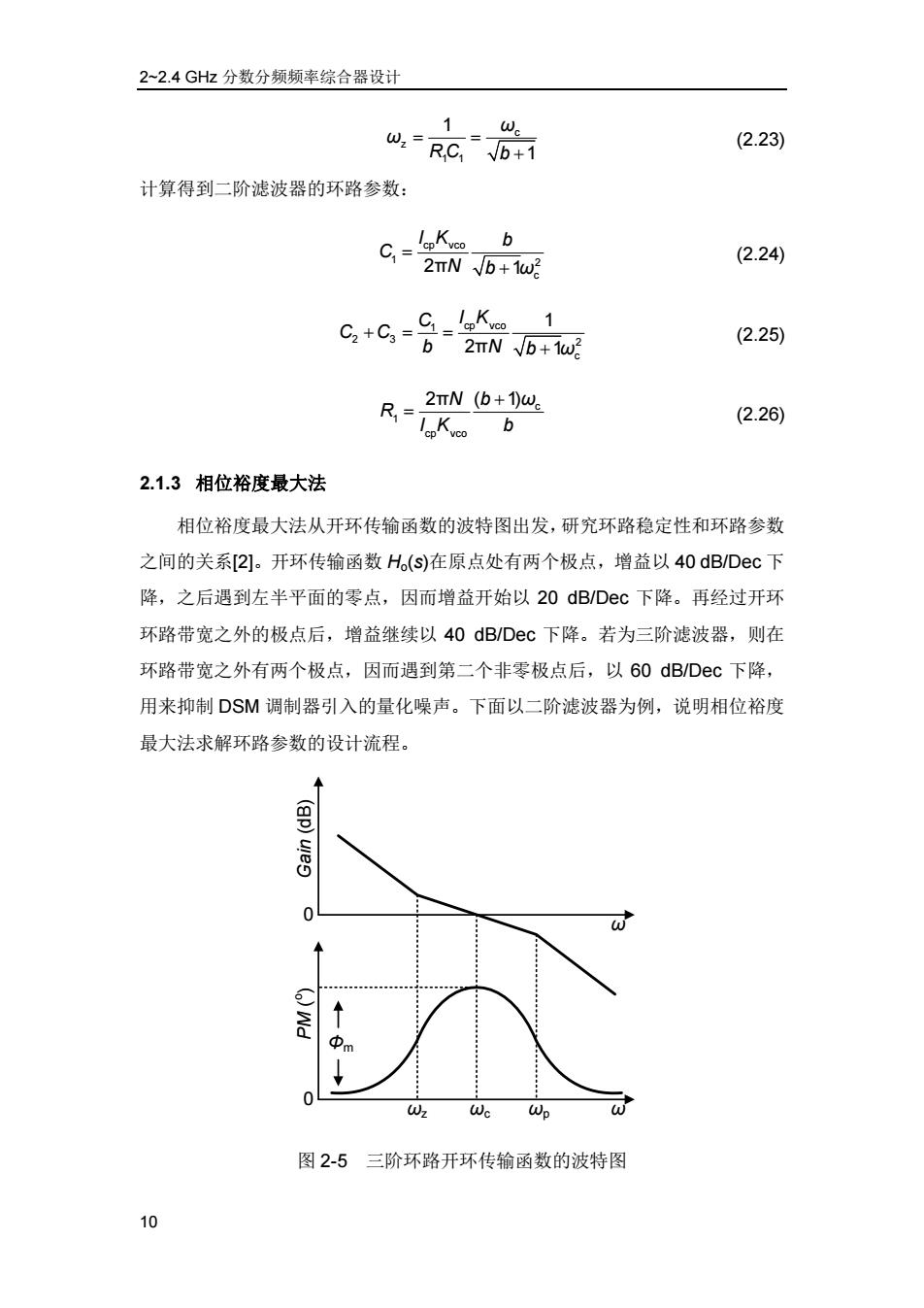
2~2.4 GHz 分数分频频率综合器设计 10 c z 1 1 1 1 ω ω R C b (2.23) 计算得到二阶滤波器的环路参数: cp vco 1 2 c 2π 1 I K b C N b ω (2.24) 1 cp vco 2 3 2 c 1 2π 1 C I K C C b N b ω (2.25) c 1 cp vco 2πN ( 1) b ω R IK b (2.26) 2.1.3 相位裕度最大法 相位裕度最大法从开环传输函数的波特图出发,研究环路稳定性和环路参数 之间的关系[2]。开环传输函数 Ho(s)在原点处有两个极点,增益以 40 dB/Dec 下 降,之后遇到左半平面的零点,因而增益开始以 20 dB/Dec 下降。再经过开环 环路带宽之外的极点后,增益继续以 40 dB/Dec 下降。若为三阶滤波器,则在 环路带宽之外有两个极点,因而遇到第二个非零极点后,以 60 dB/Dec 下降, 用来抑制 DSM 调制器引入的量化噪声。下面以二阶滤波器为例,说明相位裕度 最大法求解环路参数的设计流程。 Gain (dB) PM ( o ) 0 0 ωz ωc ωp Φm ω ω 图 2-5 三阶环路开环传输函数的波特图

第二章环路参数与相位噪声分析 如图2-5所示,开环传输函数在零点处有两个极点,因而相移为180°,相 位裕度为0°。滤波器电阻和电容的串联支路引入左半平面的零点ω2,相移减小, 相位裕度增加。由于滤波器并联电容支路引入了一个极点w,相移增加,相位 裕度减小。因此,在零点和极点之间相移最小。如果把开环带宽ω。设置在相移 最小的点,那么就可以获得环路最大的相位裕度,环路具有最佳的稳定性。由式 (2.4)可以得出,在开环带宽wc处,环路的相位裕度: (w)=arctan-arctan W (2.27) W2 为了求得最大相位裕度,两边进行求正切和求导运算: w./w2-w/w) a (tan((w))) 1+w/w2W。=0 (2.28) ow. 8w. 得 w。=Vw,w。=Vb+1w2 (2.29) 此时最大相位裕度: Pm.max arctanb+1-arctan1/b+1 (2.30) 如果用相位裕度最大法设置环路参数,环路相位裕度只与滤波器电容比值有 关。b越大,相位裕度越大,环路就越稳定。环路相位裕度最大法和根轨迹方法 尽管分析方法不一样,但得到的开环带宽和零极点的关系是一样的,因而计算得 到的滤波器参数是完全相同的。 三阶滤波器的传输函数[2]: (s)=1 1+RCS 5 RRC.C.C.s+[R.C.(C.+C3)+RjCj(C.+C.)Js+C,+Cz+C(2.31) 假设电容C2=C3,传输函数可以简化为: (1+) 1 Z3h(S) sC,+C2+C)(1+sX1+s) (2.32) Wp3 其中 11
第二章 环路参数与相位噪声分析 11 如图 2-5 所示,开环传输函数在零点处有两个极点,因而相移为 180°,相 位裕度为 0°。滤波器电阻和电容的串联支路引入左半平面的零点 ωz,相移减小, 相位裕度增加。由于滤波器并联电容支路引入了一个极点 ωp,相移增加,相位 裕度减小。因此,在零点和极点之间相移最小。如果把开环带宽 ωc 设置在相移 最小的点,那么就可以获得环路最大的相位裕度,环路具有最佳的稳定性。由式 (2.4)可以得出,在开环带宽 ωc 处,环路的相位裕度: c c m c z p ( ) arctan arctan ω ω φ ω ω ω (2.27) 为了求得最大相位裕度,两边进行求正切和求导运算: cz cp 2 m c z p c c ( ) (tan( ( ))) 1 0 c ωω ωω φ ω ω ωω ω ω (2.28) 得 ω ωω c zp z b 1ω (2.29) 此时最大相位裕度: φm,max arctan 1 arctan1 1 b b (2.30) 如果用相位裕度最大法设置环路参数,环路相位裕度只与滤波器电容比值有 关。b 越大,相位裕度越大,环路就越稳定。环路相位裕度最大法和根轨迹方法 尽管分析方法不一样,但得到的开环带宽和零极点的关系是一样的,因而计算得 到的滤波器参数是完全相同的。 三阶滤波器的传输函数[2]: 1 1 F,3th 2 1 312 3 11 2 3 3 3 1 2 1 2 3 1 1 ( ) ()() RCs Z s s RRCCC s RC C C RC C C s C C C (2.31) 假设电容 C2=C3,传输函数可以简化为: z F,3th 123 p2 p3 (1+ ) 1 ( )= ( ) (1 )(1 ) s ω Z s sC C C s s ω ω (2.32) 其中