复旦大学：《微电子学与固体电子学》教学资源（硕士士学位论文）2~2.4GHz分数分频频率综合器设计

2~2.4GHz分数分频频率综合器设计 1 1 w.-RCR(C+C)bu: C2+C3 (2.33) R3C2C3 可见在电容比b=C1(C2+C3)比较大时，二阶滤波器和三阶滤波器零点相同， 环路带宽之外的第一个极点w2近似相同。唯一不同的是，三阶环路滤波器比 二阶滤波器在带外多出一个极点ω3。于是在三阶滤波器环路参数计算的过程 中，就可以先按照二阶滤波器计算出C1和C2+C3,根据第三个极点的位置就可 以直接计算出滤波器另外一个电阻值R3。 按照和二阶滤波器相同的方法，可以求得三阶滤波器参数R1和(2.26)相等， 由式(2.33)进而得到： Ckee bvn (2.34) 2πN(b+1)w2 c-4品0o9 (2.35) R 4TNw。b+1 (2.36) pleKvco b 其中p为采用三阶滤波器时，开环环路带外的第三个极点w3和开环环路带宽wc 的比值。至此可以看到，一旦电容比值b和开环环路带宽w。确定，滤波器参数 和其他的环路参数就可以计算出来。而事实上，电容比值b决定了环路的相位裕 度，而开环环路带宽ωc决定了环路的建立时间。 2.2全差分频率综合器噪声建模 在全差分频率综合器中，差分电荷泵和差分滤波器使得子模块噪声传输函数 与单端调谐频率综合器噪声传输函数相比变得较为复杂。图2-6为单端调谐频率 综合器的噪声模型。ni为输入参考时钟的相位噪声，n.div和n.o分别为分频 器相位噪声和输出的相位噪声，单位为rad2Hz。Pncp为电荷泵输出电流噪声， 单位为AHz。Vnpt为滤波器输出电压噪声，单位为V2Hz。n.vco为压控振荡 器输出相位噪声，单位为rad/Hz。各个子模块到输出的噪声传输函数分别为： H(s)-9e-2I NH,(s) (2.37) Incp lop1+H。(s) 12

2~2.4 GHz 分数分频频率综合器设计 12      2 3 z p2 z p3 11 1 2 3 3 2 3 1 1 ( ) C C ω ω bω ω RC R C C RCC (2.33) 可见在电容比 b=C1/(C2+C3)比较大时，二阶滤波器和三阶滤波器零点相同， 环路带宽之外的第一个极点 ωp2 近似相同。唯一不同的是，三阶环路滤波器比 二阶滤波器在带外多出一个极点 ωp3。于是在三阶滤波器环路参数计算的过程 中，就可以先按照二阶滤波器计算出 C1 和 C2+C3，根据第三个极点的位置就可 以直接计算出滤波器另外一个电阻值 R3。 按照和二阶滤波器相同的方法，可以求得三阶滤波器参数 R1和(2.26)相等， 由式(2.33)进而得到： 3 2 cp vco 1 2 2π c ( 1) I K b C N b ω   (2.34) 1 cp vco 2 3 2 2 4π c ( 1) C I K b C C b Nb ω    (2.35) c 3 cp vco 4πNω b 1 R pI K b   (2.36) 其中 p 为采用三阶滤波器时，开环环路带外的第三个极点 ωp3和开环环路带宽 ωc 的比值。至此可以看到，一旦电容比值 b 和开环环路带宽 ωc确定，滤波器参数 和其他的环路参数就可以计算出来。而事实上，电容比值 b 决定了环路的相位裕 度，而开环环路带宽 ωc 决定了环路的建立时间。 2.2 全差分频率综合器噪声建模 在全差分频率综合器中，差分电荷泵和差分滤波器使得子模块噪声传输函数 与单端调谐频率综合器噪声传输函数相比变得较为复杂。图 2-6 为单端调谐频率 综合器的噪声模型。θ2 n,i 为输入参考时钟的相位噪声，θ2 n,div 和 θ2 n,o 分别为分频 器相位噪声和输出的相位噪声，单位为 rad2 /Hz。i 2 n,cp 为电荷泵输出电流噪声， 单位为 A2 /Hz。v2 n,lpf 为滤波器输出电压噪声，单位为 V2 /Hz。θ2 n,vco为压控振荡 器输出相位噪声，单位为 rad2 /Hz。各个子模块到输出的噪声传输函数分别为：    n,o o cp n,cp cp o 2π ( ) ( ) 1 () θ NH s H s i I Hs (2.37)

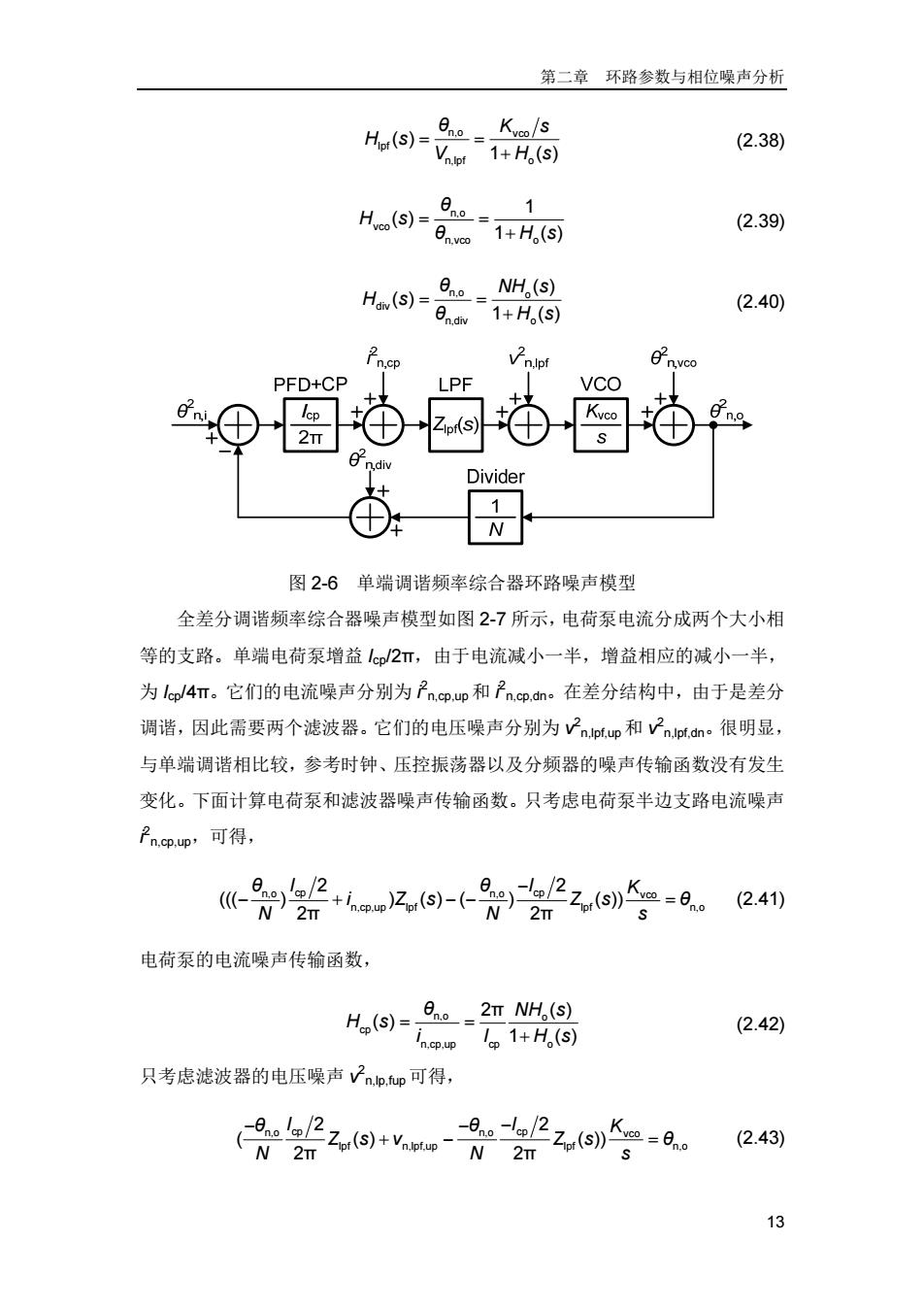
第二章环路参数与相位噪声分析 6n0- Kvo/s H,s)=e1+H.⑨) (2.38) Hs)= 9n。= 1 1+H(S) (2.39) Haiv (S)=- exo NH (s) n1+H(S) (2.40) nvco PFD+CP LPF VCo Zpr(S) Kvco Divider 1 W 图2-6单端调谐频率综合器环路噪声模型 全差分调谐频率综合器噪声模型如图2-7所示，电荷泵电流分成两个大小相 等的支路。单端电荷泵增益1c2π，由于电流减小一半，增益相应的减小一半， 为lep/4T。它们的电流噪声分别为子ncp.p和子ncp.dn。在差分结构中，由于是差分 调谐，因此需要两个滤波器。它们的电压噪声分别为n.pfup和n.Jp.dn。很明显， 与单端调谐相比较，参考时钟、压控振荡器以及分频器的噪声传输函数没有发生 变化。下面计算电荷泵和滤波器噪声传输函数。只考虑电荷泵半边支路电流噪声 Pn.cp.up'可得， -2aw2间-0会22s-0. (2.41) 电荷泵的电流噪声传输函数， 片(S)= 9。-2TNH,(S) In.cp.up Icp 1+H(s) (2.42) 只考虑滤波器的电压噪声Vnp,p可得， 是222回，是会2z-a (2.43) N2π 13

第二章 环路参数与相位噪声分析 13 n,o vco lpf n,lpf o ( ) 1 () θ K s H s V Hs    (2.38) n,o vco n,vco o 1 ( ) 1 () θ H s θ H s    (2.39) n,o o div n,div o ( ) ( ) 1 () θ NH s H s θ H s    (2.40) 图 2-6 单端调谐频率综合器环路噪声模型 全差分调谐频率综合器噪声模型如图 2-7 所示，电荷泵电流分成两个大小相 等的支路。单端电荷泵增益 Icp/2π，由于电流减小一半，增益相应的减小一半， 为 Icp/4π。它们的电流噪声分别为 i 2 n,cp,up 和 i 2 n,cp,dn。在差分结构中，由于是差分 调谐，因此需要两个滤波器。它们的电压噪声分别为 v2 n,lpf,up和 v2 n,lpf,dn。很明显， 与单端调谐相比较，参考时钟、压控振荡器以及分频器的噪声传输函数没有发生 变化。下面计算电荷泵和滤波器噪声传输函数。只考虑电荷泵半边支路电流噪声 i 2 n,cp,up，可得， n,o n,o cp cp vco n,cp,up lpf lpf n,o 2 2 ((( ) ) ( ) ( ) ( )) 2π 2π θ θ I I K i Zs Zs θ N Ns      (2.41) 电荷泵的电流噪声传输函数，    n,o o cp n,cp,up cp o 2π ( ) ( ) 1 () θ NH s H s i I Hs (2.42) 只考虑滤波器的电压噪声 v2 n,lp,fup 可得， n,o n,o cp cp vco lpf n,lpf,up lpf n,o 2 2 ( ( ) ( )) 2π 2π θ θ I I K Zs v Zs θ N Ns      (2.43)

2~2.4GHz分数分频频率综合器设计 滤波器的电压噪声传输函数， Hpt(s)=- 9。- Kvco/s (2.44) piup 1+H(S) n.cp.up V子n.lpf.up PFD+CP LPF Iop/2 Zipf(S) f子nvoo 2m n.cp.dn n,lpf.dn -lcp/2 Zipf(S) 2T Divider N 图2-7全差分调谐频率综合器噪声模型 在差分调谐结构中，电荷泵电流噪声传输函数和滤波器噪声传输函数与单端 调谐相比并没有发生变化。因此差分调谐和单端调谐的噪声传输函数完全相同。 电荷泵输出电流噪声对输出的相位噪声贡献为： 民。ep=(匠pup+incp( 2TT NH (S))2 p1+H。(S) (2.45) 在全差分调谐结构中，电荷泵电流被分成大小相同的两部分，输出电流噪声 ncpp和子np.dn相等，为单端调谐时输出电流噪声的一半。因此，与单端调谐 结构相比，电荷泵对输出的相位噪声贡献没有发生变化。 滤波器输出电压噪声对对输出的相位噪声贡献为： O脱opr=(u+p) Kvco/S)2 1+H(S) (2.46) 在差分结构中，需要使用两个完全相同的滤波器，电压噪声Vn.lpf.up和Vn.lpf.dn 与单端调谐时电压噪声大小相等，那么差分滤波器对输出的相位噪声贡献是单端 调谐结构的两倍。 14

2~2.4 GHz 分数分频频率综合器设计 14 滤波器的电压噪声传输函数， n,o vco lpf n,lpf,up o ( ) 1 () θ K s H s v Hs    (2.44) -Icp/2 2π 1 N θ2 n,i Zlpf(s) Divider Icp/2 2π Kvco s PFD+CP Zlpf(s) i 2 n,cp,up LPF v2 n,lpf,up v2 i n,lpf,dn 2 n,cp,dn θ2 n,vco θ2 n,o θ2 n,div 图 2-7 全差分调谐频率综合器噪声模型 在差分调谐结构中，电荷泵电流噪声传输函数和滤波器噪声传输函数与单端 调谐相比并没有发生变化。因此差分调谐和单端调谐的噪声传输函数完全相同。 电荷泵输出电流噪声对输出的相位噪声贡献为： 2 22 2 o n,o,cp n,cp,up n,cp,dn cp o 2π ( ) ( )( ) 1 () NH s θ i i I Hs    (2.45) 在全差分调谐结构中，电荷泵电流被分成大小相同的两部分，输出电流噪声 i 2 n,cp,up 和 i 2 n,cp,dn 相等，为单端调谐时输出电流噪声的一半。因此，与单端调谐 结构相比，电荷泵对输出的相位噪声贡献没有发生变化。 滤波器输出电压噪声对对输出的相位噪声贡献为： 2 22 2 vco n,o,lpf n,lpf,up n,lpf,dn o ( )( ) 1 () K s θ v v H s    (2.46) 在差分结构中，需要使用两个完全相同的滤波器，电压噪声 v2 n,lpf,up 和 v2 n,lpf,dn 与单端调谐时电压噪声大小相等，那么差分滤波器对输出的相位噪声贡献是单端 调谐结构的两倍

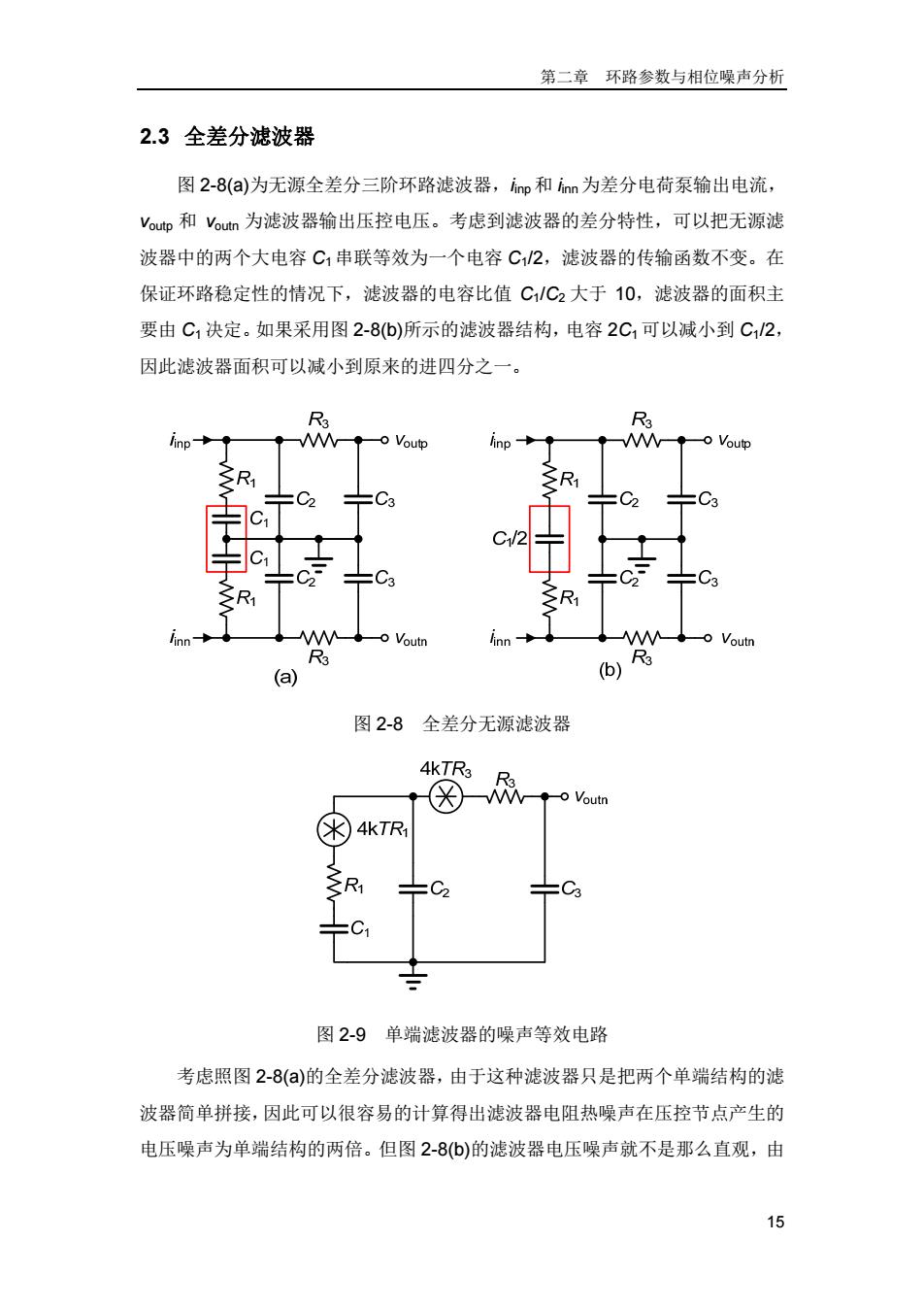
第二章环路参数与相位噪声分析 2.3全差分滤波器 图2-8(a)为无源全差分三阶环路滤波器，np和inn为差分电荷泵输出电流， Voup和vn为滤波器输出压控电压。考虑到滤波器的差分特性，可以把无源滤 波器中的两个大电容C1串联等效为一个电容C2,滤波器的传输函数不变。在 保证环路稳定性的情况下，滤波器的电容比值C/C2大于10，滤波器的面积主 要由C1决定。如果采用图2-8(b)所示的滤波器结构，电容2C1可以减小到C12, 因此滤波器面积可以减小到原来的进四分之一。 R R3 o Voutp 乞R R =C2 =C2 c -C 3R1 R inn Mo Voutn R3 R3 (a) (b) 图2-8 全差分无源滤波器 4kTR3 oVoutn 米 4kTR ÷C 图2-9单端滤波器的噪声等效电路 考虑照图2-8()的全差分滤波器，由于这种滤波器只是把两个单端结构的滤 波器简单拼接，因此可以很容易的计算得出滤波器电阻热噪声在压控节点产生的 电压噪声为单端结构的两倍。但图2-8b)的滤波器电压噪声就不是那么直观，由 15

第二章 环路参数与相位噪声分析 15 2.3 全差分滤波器 图 2-8(a)为无源全差分三阶环路滤波器，iinp 和 iinn为差分电荷泵输出电流， voutp 和 voutn 为滤波器输出压控电压。考虑到滤波器的差分特性，可以把无源滤 波器中的两个大电容 C1串联等效为一个电容 C1/2，滤波器的传输函数不变。在 保证环路稳定性的情况下，滤波器的电容比值 C1/C2 大于 10，滤波器的面积主 要由 C1决定。如果采用图 2-8(b)所示的滤波器结构，电容 2C1可以减小到 C1/2， 因此滤波器面积可以减小到原来的进四分之一。 图 2-8 全差分无源滤波器 图 2-9 单端滤波器的噪声等效电路 考虑照图 2-8(a)的全差分滤波器，由于这种滤波器只是把两个单端结构的滤 波器简单拼接，因此可以很容易的计算得出滤波器电阻热噪声在压控节点产生的 电压噪声为单端结构的两倍。但图 2-8(b)的滤波器电压噪声就不是那么直观，由

2~2.4GHz分数分频频率综合器设计 于电容C12的存在，使得上下两个滤波器关联，那么直接求出电压噪声的表达 式非常困难。 图2-9为单端滤波器的噪声等效电路，为了计算方便，令： A-R+G8-R+Gc-G0-d sC3 (2.47) 电阻R1在输出端产生的电压噪声： R+训 1 Vn.Out.R1=14kTR- sC3 SC2 sC3 11R+ 1 (2.48) +(R3+ sC sC3 sC2 sCa 即： AlIC D VoR=4KTR,B+AIIC A (2.49) 化简可得： Vo(S)=4KTR AB+AC+BC CD (2.50) 电阻R3在输出端产生的电压噪声： 1 Vn.OuLR3 =V4k TR3- SC3 (2.51) R+G+R+ 1 sC, 即： Vno=4kTR3 A+BlIC (2.52) 化简可得： -K顶B9A82ac (2.53) 16

2~2.4 GHz 分数分频频率综合器设计 16 于电容 C1/2 的存在，使得上下两个滤波器关联，那么直接求出电压噪声的表达 式非常困难。 图 2-9 为单端滤波器的噪声等效电路，为了计算方便，令： 3 1 3 123 1 111 AR BR C D sC sC sC sC      ， ，， (2.47) 电阻R1在输出端产生的电压噪声： 3 32 3 n,out,R1 1 13 3 1 32 3 11 1 ( )// 4k 1 11 1 ( )// R sC sC sC v TR RR R sC sC sC sC      (2.48) 即： n,out,R1 1 //C 4k //C A D v TR BA A   (2.49) 化简可得： n,out,R1 1 ( ) 4k CD v s TR AB AC BC    (2.50) 电阻 R3在输出端产生的电压噪声： 3 n,out,R3 3 3 1 3 12 1 4k 1 11 ( )// sC v TR R R sC sC sC    (2.51) 即： n,out,R3 3 4k //C D v TR A B   (2.52) 化简可得： n,out,R3 3 ( ) 4k B CD v TR AB AC BC     (2.53)