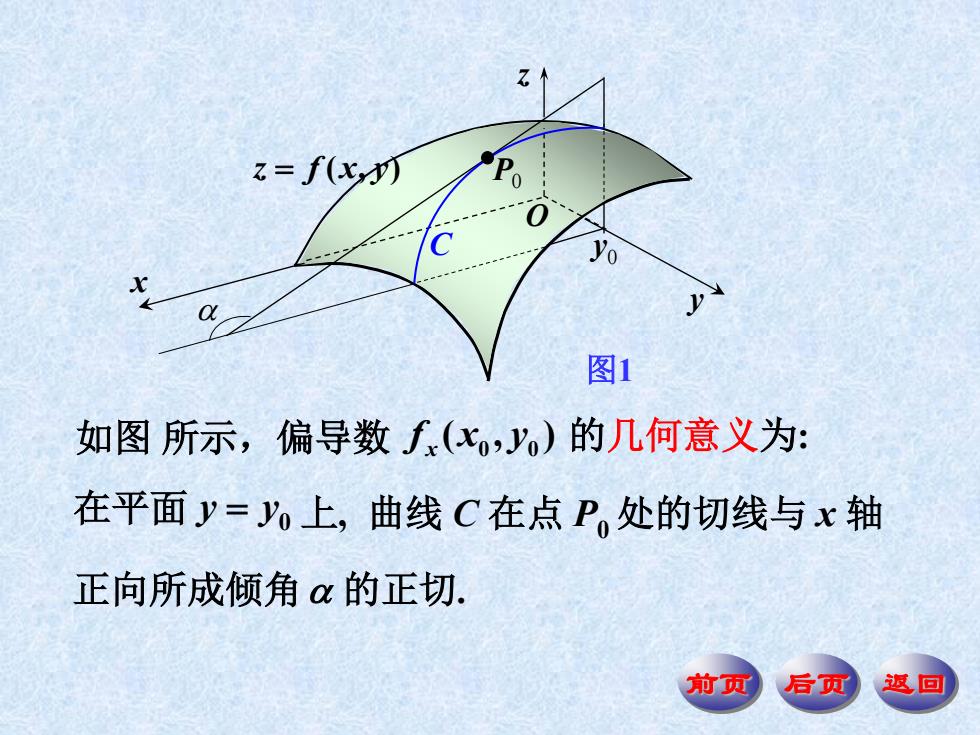
z=f(x,y) 图1 如图所示,偏导数f(x,y)的几何意义为: 在平面y=上,曲线C在点P,处的切线与x轴 正向所成倾角a的正切. 前页 后页 返回
前页 后页 返回 如图 所示,偏导数 0 0 ( , ) x f x y 的几何意义为: 在平面 0 y y 上, 曲线 C 在点 P0 处的切线与 x 轴 正向所成倾角 的正切. x y z O P0 0 y z f x y ( , ) C 图1

例2求函数f(xy)=x3+2x2y-y3在点(1,3)处关 于x和关于y的偏导数, 例3求函数z=x'(x>0)的偏导数. 4段心n-平+山 0x2+y2=0 求fx(x,y),f(x,) 前页 后页 返回
前页 后页 返回 例2 3 2 3 求函数 在点 处关 f x y x x y y ( , ) 2 (1,3) 于 x 和关于 y 的偏导数. 例3 求函数 ( 0) y z x x 的偏导数. 例4 设 0, 0 , 0, ( , ) 2 2 2 2 2 2 x y x y x y xy f x y 求 f (x, y), f (x, y). x y

三、可微性条件 由可微定义易知:若f在点P(x,y)可微,则f在 ,必连续.这表明: 连续是可微的一个必要条件. 定理17.1若二元函数f在其定义域内一点(x,yo) 处可微,则f在该点关于每个自变量的偏导数都存 在,且()式中的 A=f(xo,vo),B=f(xo2yo) 前页 后页 返回
前页 后页 返回 三、可微性条件 0 0 0 由可微定义易知: 若 f P x y f 在点 可微 则 在 ( , ) , P0 必连续.这表明: 连续是可微的一个必要条件. 定理17.1 若二元函数 f 在其定义域内一点 ( x0 , y0 ) 处可微, 则 f 在该点关于每个自变量的偏导数都存 在 ,且(1) 式中的 0 0 0 0 ( , ) , ( , ). A f x y B f x y x y

于是,函数在点(x,y)的全微分(2)可惟一地表 示为 df(xoyo)=f(xo,yo)△x+f,(xo,yo)△y 则全微分又可写为 df(Xo>Yo)=f(xo>Yo)dx+f(xoYo)dy. (△x=dx,△y=dy) 前页 后页 返回
前页 后页 返回 于是, 函数 0 0 f x y 在点( , ) 的全微分(2)可惟一地表 示为 d ( , ) ( , ) ( , ) . 0 0 0 0 0 0 x y f x y f x y x f x y y ( d , d ) x x y y 则全微分又可写为 d ( , ) ( , )d ( , )d . 0 0 0 0 0 0 x y f x y f x y x f x y y

若函数f在区域D的每一点(化,y)都可微,则称函 数f在区域D上可微,且f在D上的全微分为 df(x,y)=f(x,y)dx+f(x,y)dy. 定理17.1的应用:对于函数 f(xy)=x+y, 由于f(x,0)=|x,f0,y)=|y,它们分别在x=0 与y=0都不可导,即f(0,0)与f,(0,0)都不存在, 故f(x,y)在点(0,0)不可微. 前 后 返回
前页 后页 返回 若函数 f 在区域 D 的每一点 (x, y) 都可微, 则称函 数 f 在区域 D 上可微,且 f 在 D 上的全微分为 d ( , ) ( , )d ( , )d . x y f x y f x y x f x y y 定理17. 1 的应用: 对于函数 2 2 f x y ( , ) , x y 由于 f x x f y y ( ,0) | |, (0, ) | |, 它们分别在 x 0 与 y 0 (0,0) x 都不可导,即 f 与 (0,0) , y f 都不存在 故 f x y ( , ) (0,0) . 在点 不可微