
尔5考察函颈)'+产20 y 0,x2+y2=0 在原点的可微性. 定理17.2(可微的充分条件)若函数z=f(x,y)在 点P(x,y)的某邻域内存在偏导数fx与f,且它 们在点P连续,则f在点P可微. 前页 后页 返回
前页 后页 返回 在原点的可微性. 2 2 2 2 2 2 , 0, ( , ) 0, 0 xy x y f x y x y x y 例5 考察函数 定理 17.2 (可微的充分条件) 若函数 z f x y ( , ) 在 0 0 0 P x y ( , ) , x y 点 的某邻域内存在偏导数 f f 与 且它 P0 f 们在点 连续 在点 P0 , 则 可微

例3中的函数z=x'在{(x,y)川x>0,-0<y<+∞} 上满足定理17.2的条件,亦在其定义域上可微 注意偏导数连续并不是可微的必要条件,例如 x2+y2=0. 它在原点(0,0)处可微,但∫x与f,却在该点不连续 前页 后页 返回
前页 后页 返回 3 {( , ) | 0, } y 例 中的函数 在 z x x y x y 上满足定理 17.2 的条件, 亦在其定义域上可微. 注意 偏导数连续并不是可微的必要条件,例如 2 2 2 2 2 2 2 2 1 ( )sin , 0, ( , ) 0, 0. x y x y f x y x y x y 它在原点(0,0)处可微, 但 x y f f 与 却在该点不连续

若f(x,y)的偏导数f与f在点(xy)都连续,则 称f在点(,y)连续可微. 定理17.3设函数f在点(x,y)的某邻域内存在偏 导数,若(,y)属于该邻域,则存在 5=+81(x-x)和n=y0+02(y-y), 0<0,02<1, 使得 f(x,y)-f(xo,vo)=f(s,y)(x-xo) +,(xo)(0y-yo) 前页 后页 返回
前页 后页 返回 f x y ( , ) 0 0 若 的偏导数 f f x y 与 在点( , ) x y 都连续, 则 0 0 称 在点 f x y ( , ) 连续可微. 导数,若 属于该邻域 则存在 ( , ) , x y 0 0 0 0 0 ( , ) ( , ) ( , ) ( ) ( , ) ( ). x y f x y f x y f y x x f x y y 0 0 定理 17.3 设函数 f x y 在点( , ) 的某邻域内存在偏 1 2 0 , 1, x x x 0 1 0 ( ) 和 0 2 0 y y y ( ), 使得
四、可微性的几儿何意义及应用 定义3设曲面S上一 点P,Ⅱ为通过点P的 一个平面,S上的动点 2到定点P和到平面Ⅱx 图2 的距离分别记为d和h.若当2在S上以任意方式 老近于P时,恒有鲁0 则称Ⅱ为曲面S在点P的切平面,称P为切点. 返回
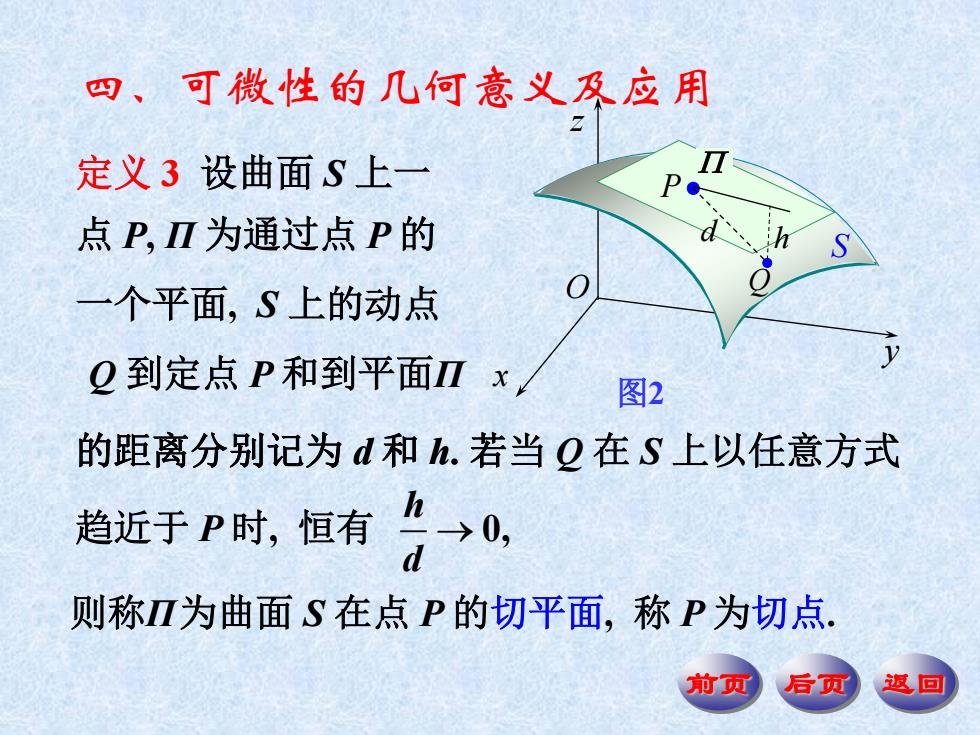
前页 后页 返回 四、可微性的几何意义及应用 定义 3 设曲面 S 上一 一个平面, S 上的动点 P Q d h x y z O S 点 P, Π 为通过点 P 的 的距离分别记为 d 和 h. 若 趋近于 P 时, 恒有 的距离分别记为 d 和 h. 若当 Q 在 S 上以任意方式 Q 到定点 P 和到平面Π 0, h d 则称Π为曲面 S 在点 P 的切平面, 称 P 为切点. 图2

定理17.4曲面z=f(x,y)在点P(x0y0,f(x,y) 存在不平行于z轴的切平面的充要条件是:函数f 在点P(x,y)可微. 定理17.4说明:函数在点(x,)可微,则曲面 z=f(,y)在点P(x,)处的切平面方程为 z-0=(x,y)x-x)+f,(xo,y)y-y0). 前页 后页 返回
前页 后页 返回 定理 17.4 曲面 0 0 0 0 z f x y P x y f x y ( , ) ( , , ( , )) 在点 存在不平行于 z 轴的切平面的充要条件是: 函数 f 在点 0 0 0 P x y ( , ) 可微. 0 0 0 定理 17.4 说明: 函数 在点 P x y ( , ) 可微, 则曲面 0 0 0 z f x y P x y z ( , ) ( , , ) 在点 处的切平面方程为 0 0 0 0 0 0 0 ( , )( ) ( , )( ). x y z z f x y x x f x y y y