
二、导数的定义 定义1.设函数y=f(x)在点x,的某邻域内有定义 若 1imf)-fo)=1imAy △y=f(x)-f(x》 X→x0 x-X0 △x→0△X △X=X-X0 存在,则称函数f(x)在点x处可导, 并称此极限为 y=∫(x)在点x。的导数记作 w器- df(x) dx =xo 即 x=f(xo)lim,Ay Ax→0△X lim f(x,+△x)-(xo) lim f(xo+h)-f(xo) △x→0 △x -→0 HIGH EDUCATION PRESS 凯动目录上页下页返回结束
二、导数的定义 定义1 . 设函数 在点 0 lim x→x 0 0 ( ) ( ) x x f x f x − − x y x = →0 lim ( ) ( )0 y = f x − f x 0 x = x − x 存在, 并称此极限为 记作: ; 0 x x y = ( ) ; 0 f x ; d d 0 x x x y = d 0 d ( ) x x x f x = 即 0 x x y = ( ) 0 = f x x y x = →0 lim 则称函数 若 的某邻域内有定义 , 在点 处可导, 在点 的导数. 机动 目录 上页 下页 返回 结束
运动质点的位置函数S=f(t) f(,) 在t时刻的瞬时速度 v lim f()-f()」 1→10 t-to 曲线C:y=f(x)在M点处的切线斜率 =lim f(x)-f(x)】 y x→x0 x-Xo f(xo) HIGH EDUCATION PRESS ◆0C08 机动目录上页下页返回结束
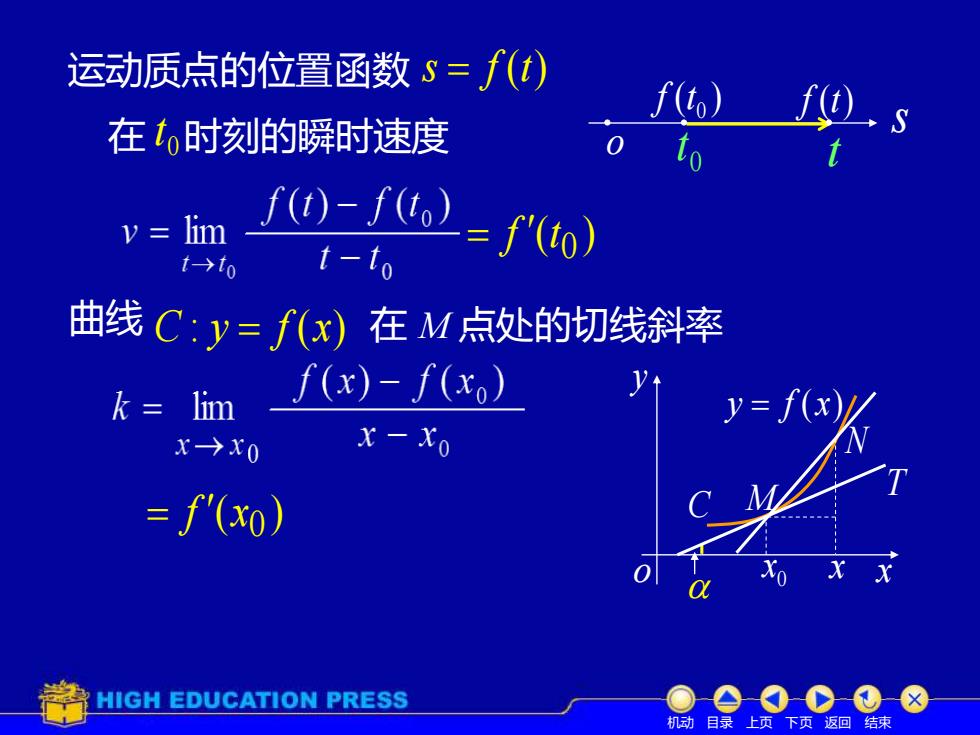
运动质点的位置函数 s = f (t) s o 0 t ( )0 f t f (t) 在 时刻的瞬时速度 t 0 t 曲线 C : y = f (x) 在 M 点处的切线斜率 x y o y = f (x) C N T 0 x M x ( ) 0 = f t ( ) 0 = f x 机动 目录 上页 下页 返回 结束

lim f(x)-∫() lim △y △y=f(x)-f(x) x→x0 x-xo △x→0△X △X=X-X0 若上述极限不存在,就说函数在点x不可导 若1imy=0,也称/()在xo的导数为无穷大 △x>0△X 若函数在开区间1内每点都可导,就称函数在1内可导 此时导数值构成的新函数称为导函数 记作y:): .df(x) d ’dx 注意)==≠ dx HIGH EDUCATION PRESS 机动目录上页下页返回结束
( ) ( )0 y = f x − f x 0 x = x − x 若上述极限不存在 , 在点 不可导. 0 x 若 lim , 0 = → x y x 也称 在 若函数在开区间 I 内每点都可导, 此时导数值构成的新函数称为导函数. 记作: y ; f (x) ; ; d d x y . d d ( ) x f x 注意: ( )0 f x 0 ( ) x x f x = = x f x d d ( ) 0 就说函数 就称函数在 I 内可导. 的导数为无穷大 . 机动 目录 上页 下页 返回 结束

例1.求函数f(x)=C(C为常数)的导数 解:y=imfx+Aw)-f1im C-C =0 △x→0 △x △x→0△X 即 (C)y'=0 例2.求函数f(x)=x”(n∈N)在x=a处的导数, 解:f'o)=lmf)-f@=1im-a x-→a x-a x→ax-a =lim(x"-+ax"-2+a2x"-3+.+a-l) x→a =nan-l HIGH EDUCATION PRESS 机动目录上页下页返回结束
例1. 求函数 (C 为常数) 的导数. 解: y 即 例2. 求函数 解: x a f x f a − ( ) − ( ) x→a = lim x a x a n n x a − − = → lim lim( x→a = n−1 x −2 + n a x 2 −3 + n a x + ) −1 + n a x f x x f x ( + ) − ( ) 0 lim → = x 机动 目录 上页 下页 返回 结束