
第之节 第三章 岛数图形的描狯 曲线的渐近线 二、函数图形的描绘 HIGH EDUCATION PRESS 机动目录上页下页返回结束
第六节 一、 曲线的渐近线 二、 函数图形的描绘 机动 目录 上页 下页 返回 结束 函数图形的描绘 第三章

一、 水平与铅直渐近线 若1imf(x)=b,则曲线y=f(x)有水平渐近线y=b X→+00 (或x→-o) 若1imf(x)=o,则曲线y=f(x)有垂直渐近线 x=X0 x→x0 (或x→x) 例1.求曲线y= +2的渐近线 x-1 解:1im(1,+2)=2 X→0x-1 .y=2为水平渐近线 阿2)=,.=1为垂直近线 HIGH EDUCATION PRESS 机动目录上页下页返回结束
一、 水平与铅直渐近线 若 则曲线 有水平渐近线 y = b. (或x → −) 若 则曲线 有垂直渐近线 . 0 x = x ( ) 0 → − 或x x 例1. 求曲线 的渐近线 . 解: 2) 2 1 1 lim ( + = x→ x − y = 2 为水平渐近线; 2) , 1 1 lim( 1 + = x→ x − x =1 为垂直渐近线. 2 1 机动 目录 上页 下页 返回 结束

二、 函数图形的描绘 步骤: 1.确定函数y=f(x)的定义域,并考察其对称性及周 期性; 2.求f'(x),f"(x),并求出f'(x)及f"(x)为0和不存在 的点; 3.列表判别增减及凹凸区间,求出极值和拐点; 4. 求渐近线; 5.确定某些特殊点,描绘函数图形 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、函数图形的描绘 步骤 : 1. 确定函数 的定义域 , 期性 ; 2. 求 并求出 及 3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求渐近线 ; 5. 确定某些特殊点 , 描绘函数图形 . 为 0 和不存在 的点 ; 并考察其对称性及周 机动 目录 上页 下页 返回 结束
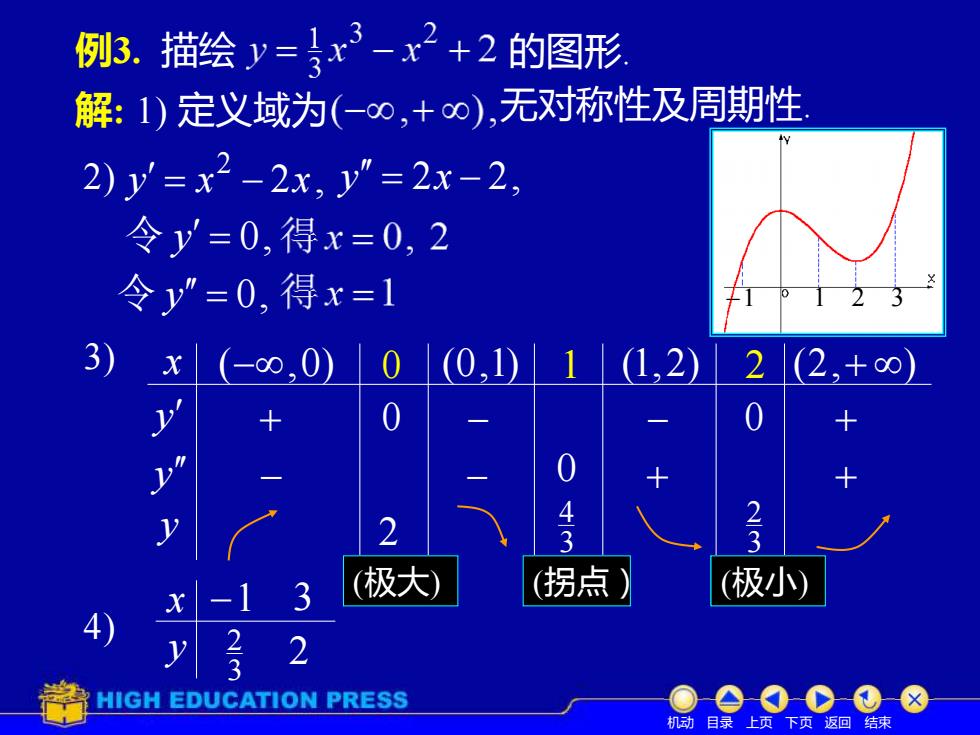
例3.描绘y=}x3-x2+2的图形 解:1)定义域为(-0,+∞),无对称性及周期性 2)y=x2-2x,y=2x-2 令y=0,得x=0,2 令y”=0,得x=1 ∞000102220 0 a 3 23 -1 3 (极大) 拐点》 (极小) 2 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例3. 描绘 的图形. 解: 1) 定义域为 无对称性及周期性. 2) 2 , 2 y = x − x y = 2x − 2, 令 y = 0, 令 y = 0, 3) x y y y (−,0) 0 (0,1) 1 (1,2) 2 (2,+ ) + 0 − − 0 + − − + + 2 3 4 (极大) (拐点) 3 2 (极小) 4) x y −1 3 3 2 2 0 机动 目录 上页 下页 返回 结束 −1 1 2 3

例5.描绘函数y=2元 的图形 解:1)定义域为(-0,+∞),图形对称于y轴 2)求关键点 y'= xe 2 √2π y 1ea-) 令y=0得x=0;令y”=0得x=±1 0 (0,1) 1,+0 3)判别曲线形态 17 0 2πe (极大) 拐点) HIGH EDUCATION PRESS 凯动目录上页下页返回结束
例5. 描绘函数 的图形. 解: 1) 定义域为 图形对称于 y 轴. 2) 求关键点 y = 2 1 − , 2 2 x x e − y = 2 1 − 2 2 x e − (1 ) 2 − x 令 y = 0得 x = 0; 令 y = 0得x = 1 机动 目录 上页 下页 返回 结束 − − − + 2 1 0 0 2 e 1 x y y y 0 (0, 1) 1 (1, + ) 3) 判别曲线形态 (极大) (拐点)