
第五节 第三章 岛数的极值与 最大值最小值 函数的极值及其求法 二、最大值与最小值问题 HIGH EDUCATION PRESS D-C①8 机动目录上页下页返回结束
二、最大值与最小值问题 一、函数的极值及其求法 第五节 机动 目录 上页 下页 返回 结束 函数的极值与 最大值最小值 第三章

函数的极值及其求法 定义:设函数f(x)在(a,b内有定义,x0∈(a,b) 若存在x,的一个邻域,在其中当x≠xo时, (1)f(x)<f(xo),则称xo为f(x)的极大点, 称f(xo)为函数的极大值, (2)f(x)>f(xo),则称xo为(x)的极小点, 称f(xo)为函数的极小值 极大点与极小点统称为极值点 HIGH EDUCATION PRESS 机动目录上页下页返回结束
一、函数的极值及其求法 定义: 在其中当 时, (1) 则称 为 的极大点 , 称 为函数的极大值 ; (2) 则称 为 的极小点 , 称 为函数的极小值 . 极大点与极小点统称为极值点 . 机动 目录 上页 下页 返回 结束
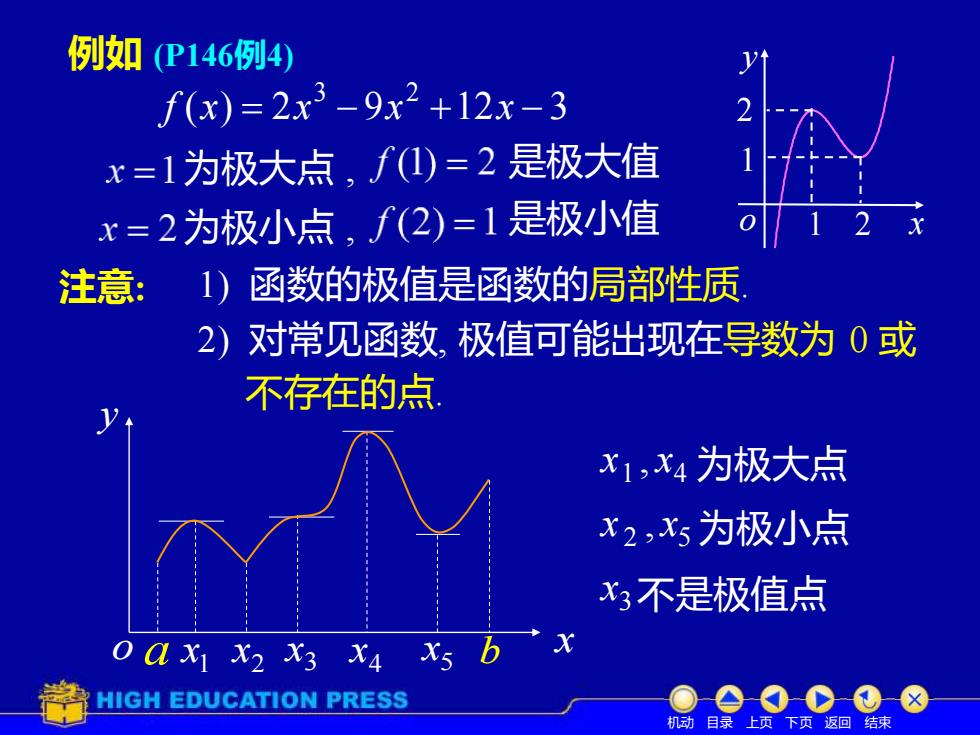
例如P146例4 f(x)=2x3-9x2+12x-3 x=1为极大点,f)=2是极大值 x=2为极小点,f(2)=1是极小值 注意: 1)函数的极值是函数的局部性质 2)对常见函数,极值可能出现在导数为0或 不存在的点 x1,x4为极大点 x2,x5为极小点 x3不是极值点 oaX1 x2 x3 xA x5 bx HIGH EDUCATION PRESS 机动目录上页下页返回结束
注意: 3 x 1 x 4 x 2 x 5 a x x o b y 1 4 x , x 为极大点 2 5 x , x 为极小点 3 x 不是极值点 2) 对常见函数, 极值可能出现在导数为 0 或 不存在的点. 1) 函数的极值是函数的局部性质. ( ) 2 9 12 3 3 2 f x = x − x + x − 例如 (P146例4) 为极大点 , 是极大值 为极小点 , 是极小值 1 2 o x y 1 2 机动 目录 上页 下页 返回 结束
定理1(极值第一判别法) 设函数f(x)在,的某邻域内连续,且在空心邻域 内有导数,当x由小到大通过x时, (1)f'(x)“左正右负”,则f(x)在x,取极大值 (2)手'(x)“左负右正”,则f(x)在x取极小值, (自证) 点击图中任意处动画播放暂停 HIGH EDUCATION PRESS 机动目录上页下页返回结束
定理 1 (极值第一判别法) ( ) , 设函数 f x 在x0的某邻域内连续 且在空心邻域 内有导数, , 当x由小到大通过 x0时 (1) f (x) “左正右负” , ( ) ; (2) f (x) “左负右正” , 则 f x 在x0 取极小值 ( ) . 则 f x 在x0 取极大值 (自证) 机动 目录 上页 下页 返回 结束 点击图中任意处动画播放\暂停

例1.求函数f(x)=(x-1)x3的极值 解)求导数了x=+(x-)子= 2)求极值可疑点 令f"(x)=0,得x1=;令f'(x)=o,得x2=0 3)列表判别 (-0,0 25 (,+∞) f'(x) f(x) 0.33 .x=0 是极大点其极大值为f(0)=0 x= 是极小点其极小值为f()=-0.33 HIGH EDUCATION PRESS 0-00C08 机动目录上页下页返回结束
例1. 求函数 的极值 . 解: 1) 求导数 = 3 + 2 f (x) x 3 1 3 2 ( 1) − x − x 3 5 2 3 5 x x− = 2) 求极值可疑点 令 f (x) = 0 , 得 ; 5 2 x1 = 令 f (x) = , 得 0 x2 = 3) 列表判别 x f (x) f (x) 0 5 2 0 + − + 0 − 0.33 (−, 0) (0 , ) 5 2 ( , ) 5 2 + 是极大点,其极大值为 是极小点,其极小值为 机动 目录 上页 下页 返回 结束