
上次课内容复习 1、无穷级数的定义;无穷级数的部分和数列; 无穷级数收敛及其发散的概念。 2、无穷级数的性质。 3、无穷级数收敛的必要条件。 4、等比级数(几何级数)的敛散性及其条件
上次课内容复习 1、无穷级数的定义;无穷级数的部分和数列; 无穷级数收敛及其发散的概念。 2、无穷级数的性质。 3、无穷级数收敛的必要条件。 4、等比级数(几何级数)的敛散性及其条件

§9.2正项级数 若4n之0,则称∑4为正项级数· 定理1正项级数 》4n收敛部分和序列Sn n=1 (n=1,2,.有界 证:> 若∑4n收敛,则{Sn收敛,故有界。 n=l .un≥0,.部分和数列{Sn}单调递增, 又已知{Sn}有界,故{Sn}收敛,从而∑4n也收敛. n三
§9.2 正项级数 若 0, un 则称 为正项级数 . n=1 un 定理1 正项级数 收敛 部分和序列 有界 . 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 单调递增, 收敛 , 也收敛. 证:

0 定理2(比较审敛法)设∑4n,∑yn是两个正项级数, n=l n=1 且存在N∈Z+,对一切n>N,有un≤kyn(常数k>0), 则有 00 00 (1)若强级数∑yn收敛,则弱级数∑4n也收敛; n=l n=l 00 (2)若弱级数入4n发散,则强级数)yn也发散. n=1 n=1
定理2 (比较审敛法) 设 且存在 对一切 有 (1) 若强级数 则弱级数 (2) 若弱级数 则强级数 则有 收敛 , 也收敛 ; 发散 , 也发散 . 是两个正项级数, (常数k >0)
例1证明级数 之2”+金 (k>0) 是收敛的。 例2讨论P一级数 1 1+2 立+.+市+.常数n0 1 的敛散性。 例3判断级数 之a+ln+④ 的敛散性
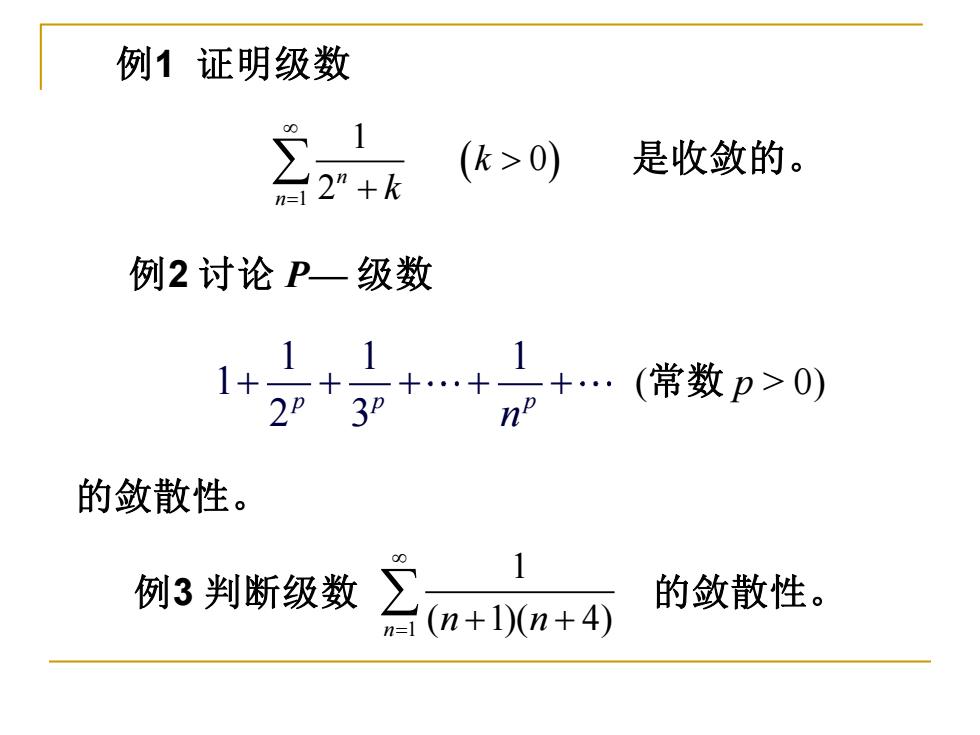
例1 证明级数 ( ) 1 1 0 2 n n k k = + 是收敛的。 1 1 1 1 2 3 p p p n + + + + + 例2 讨论 P— 级数 (常数 p > 0) 的敛散性。 例3 判断级数 的敛散性。 1 1 n ( 1)( 4) n n = + +

定理3 (比较审敛法的极限形式)设两正项级数 ∑4n,∑yn满足1im4n=l,则有 n=l n=l n-→oVn (1)当 0<时0 两个级数同时收敛或发散; 00 (2)当1=0且∑yn收敛时,∑4n也收敛; n=1 n=1 (③)当1=o且∑yn发散时,∑4n也发散. n=1 n=1
定理3 (比较审敛法的极限形式) lim l, v u n n n = → 则有 两个级数同时收敛或发散 ; 设两正项级数 满足 (1) 当 0 l 时, (2) 当 l = 0 (3) 当 l =