
无穷级数习题课 数项级数的审敛方法总结: 包括:正项级数的审敛方法; 交错级数的审敛方法; 一般项级数的审敛方法
无穷级数习题课 数项级数的审敛方法总结: 包括:正项级数的审敛方法; 交错级数的审敛方法; 一般项级数的审敛方法
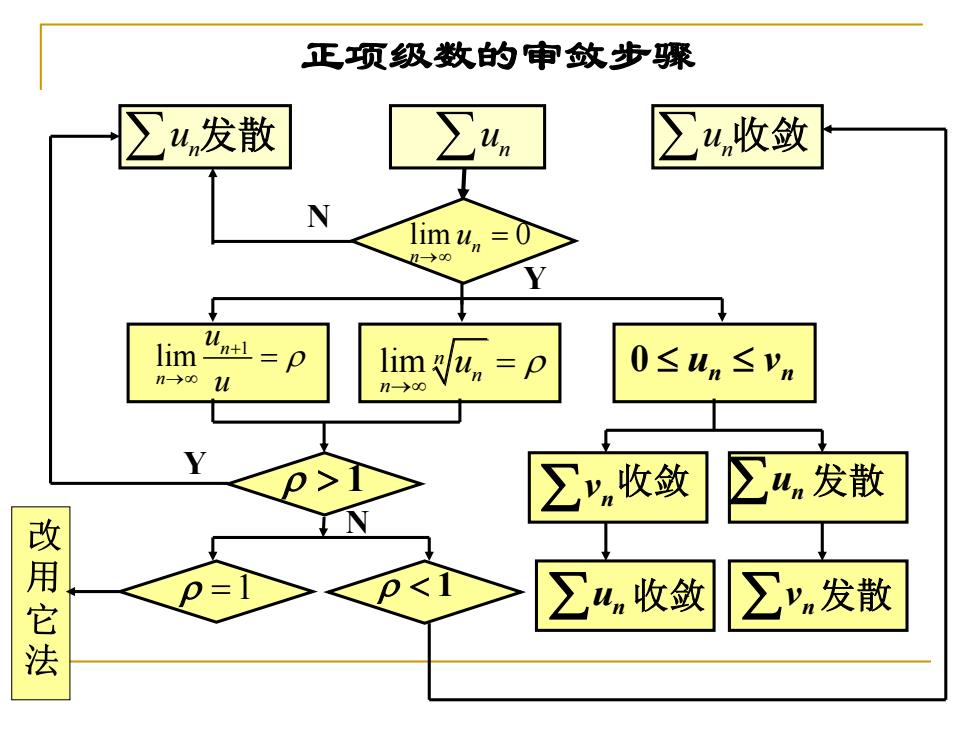
正项级数的审敛步骤 ∑4,发散 ∑4 ∑4,收敛 lim u,=0 Y lim n→00 0≤un≤yn u limu,=p ∑y收敛 ∑4n发散 改用它法 ∑un收敛 ∑yn发散
正项级数的审敛步骤 n u n u 发散 n u 收敛 lim 0 n n u → = N 1 lim n n u u + → = lim n n n u → = n n 0 u v 1 收敛 发散 收敛 n v un un n v 发散 1 Y =1 N Y
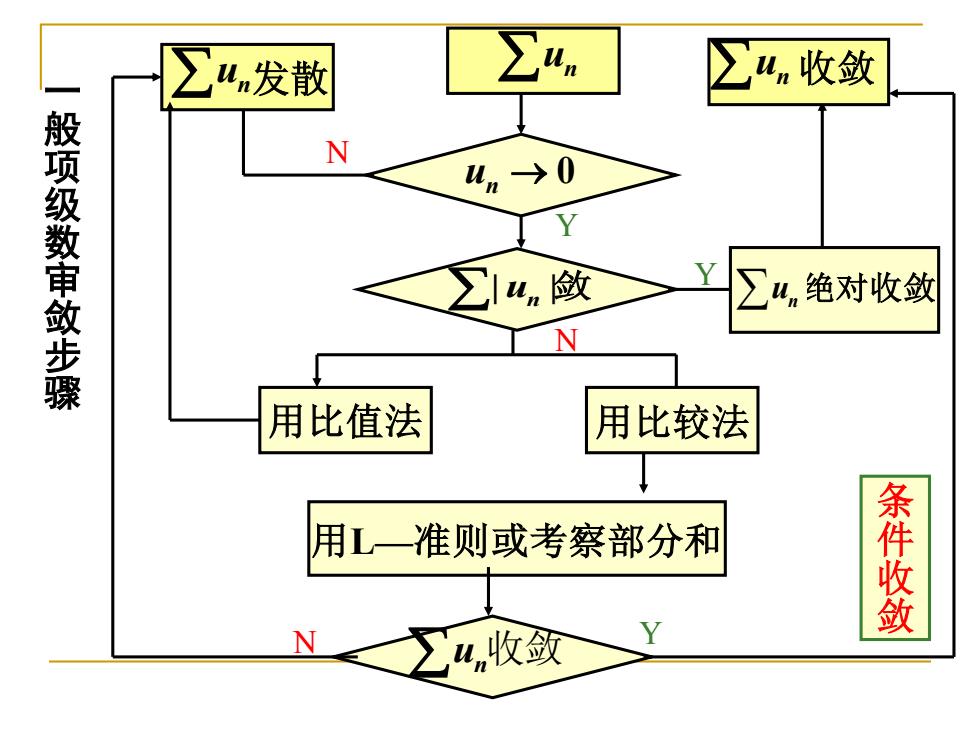
4n发散 ∑4n ∑4收敛 N 般项级数审敛步骤 4n→0 ∑14n做 ∑4,绝对收敛 N 用比值法 用比较法 用L一准则或考察部分和 条件收敛 un收敛
u n → 0 u n N u n 发散 Y | u n |敛 Y u n 绝对收敛 u n 收敛 N 用比值法 用比较法 用L—准则或考察部分和 N u n收敛 Y 条件收敛 一般项级数审敛步骤

例1判断级数 是否收敛?如果收敛, n=1 n -Inn 是条件收敛还是绝对收敛? 解 1>1 >一 n-Inn 而 发散, (-1)” 1 n=l n -Inn un-t 发散, 即原级数非绝对收敛, ,二是交级数,由来布和尼茨定理 Inn Inx ·lim n→+o∞ =lim =lim二=0, x-→+0X x→+o0X
解 , 1 ln 1 n n n − , 1 1 而 发散 n= n , ln 1 ln ( 1) 1 1 发散 = = − = − − n n n n n n n 即原级数非绝对收敛. , ln ( 1) 1 是交错级数 = − − n n n n 由莱布尼茨定理: x x n n n x ln lim ln lim →+ →+ = 0, 1 = lim = x→+ x 例1 是条件收敛还是绝对收敛? 判断级数 是否收敛?如果收敛, = − 1 ( 1) n n n −lnn

1 1 lim- lim- n-=0, n>+oon-nn n→+oo Inn n f(x)=x-Inx (x>0), f=1-1>0(x>I,在L,o)上单增, 即 单减,故1一 x-Inx 当n>1时单减, n-Inn .儿n= n-Inn (n+1)-ln(n+1) =L+1(n>1), 所以此交错级数收敛,故原级数是条件收敛
0, ln 1 1 lim ln 1 lim = − = − →+ →+ n n n n n n n f (x) = x − ln x (x 0), 0 ( 1), 1 ( ) = 1− x x f x 在 (1,+) 上单增, , ln 1 即 单减 x − x 1 , ln 1 故 当 时单减 − n n n ( 1), ( 1) ln( 1) 1 ln 1 = 1 + − + − = u + n n n n n u n n 所以此交错级数收敛,故原级数是条件收敛.