
第十章 微分方程与差分方程 探索和研究变量与变量之间的关系是社会科学与 自然科学问题中所面临的重要课题。一般而言,变量 与变量之间有如下两种关系: 1、确定性关系 立方体的体积与边长之间的关系; 自由落体运动中距离与时间的关系等。 2、随机性关系 人的身高与体重之间的关系; 人的年龄与血压之间的关系等
第十章 微分方程与差分方程 探索和研究变量与变量之间的关系是社会科学与 自然科学问题中所面临的重要课题。一般而言,变量 与变量之间有如下两种关系: 1、确定性关系 立方体的体积与边长之间的关系; 自由落体运动中距离与时间的关系等。 2、随机性关系 人的身高与体重之间的关系; 人的年龄与血压之间的关系等

微分方程是寻求具有确定性关系的变量之间的 关系的科学; 概率论与数理统计则是研究具有随机性关系的 变量之间的关系的科学。 方程的概念: 代数方程一含有未知数的方程。 微分方程一含有未知函数的导数或微分的方程
微分方程是寻求具有确定性关系的变量之间的 关系的科学; 概率论与数理统计则是研究具有随机性关系的 变量之间的关系的科学。 方程的概念: 代数方程 — 含有未知数的方程。 微分方程 — 含有未知函数的导数或微分的方程
§10.1微分方程的基本概念 引例1一曲线通过点(1,2),在该曲线上任意点 处的切线斜率为2x,求该曲线的方程. dy 方程: =2x dx yx1=2 通解:y=x2+C 特解:y=x2+1
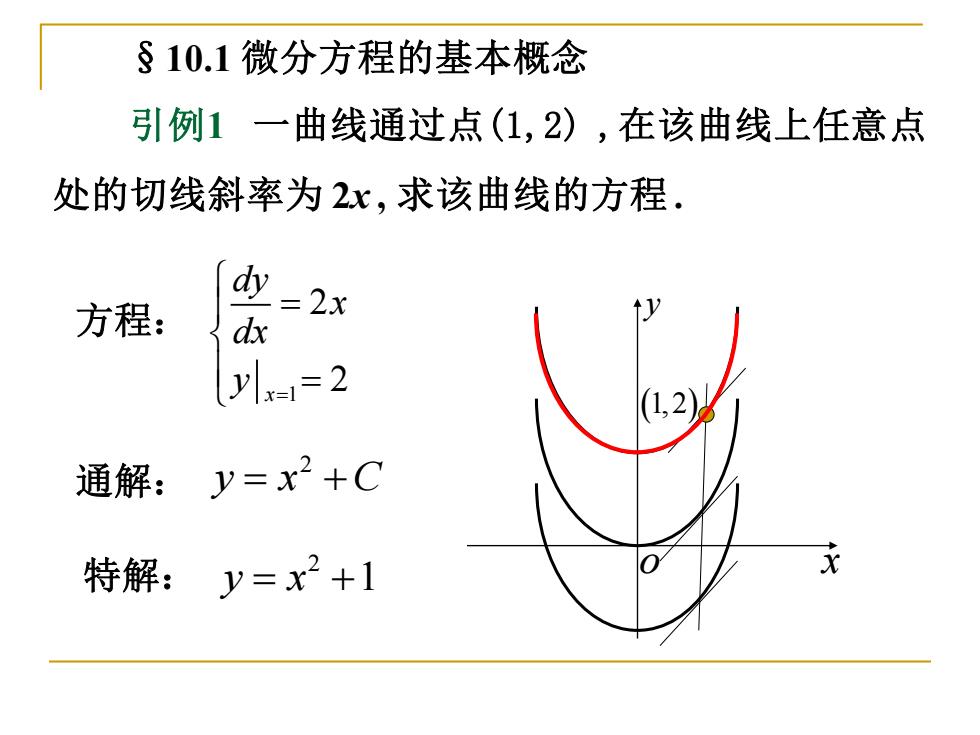
§10.1 微分方程的基本概念 引例1 一曲线通过点(1,2) ,在该曲线上任意点 处的切线斜率为 2x , 求该曲线的方程 . x y o 方程: 1 2 2 x dy x dx y = = = 通解: 2 y x C = + 特解: 2 y x = +1 (1, 2)

引例2列车在平直路上以20m/s的速度行驶, 制动时获得加速度a=-0.4m/s2,求制动后列车的 运动规律. d2s 方程: =-0.4 d:2 ds S=0=0, dtt=020 通解:s=-0.2t2+C1t+C2 特解:8=-0.2t2+20t
引例2 列车在平直路上以 的速度行驶, 制动时获得加速度 求制动后列车的 运动规律. 0 , s t=0 = 方程: 通解: 1 2 2 s = − 0.2t +C t +C 特解: s 0.2 t 20 t 2 = − +

定义1一个方程,如果含有未知函数的导数或 微分,则称该方程为微分方程;微分方程中出现的 未知函数的导数的最高阶数称为这个方程的阶.未知 函数是一元函数的微分方程称为常微分方程 未知函数是多元函数的微分方程,称为偏微分 方程 常微分方程(本章内容) 分类 偏微分方程
定义1 一个方程,如果含有未知函数的导数或 微分,则称该方程为微分方程;微分方程中出现的 未知函数的导数的最高阶数称为这个方程的阶. 未知 函数是一元函数的微分方程称为常微分方程. 未知函数是多元函数的微分方程,称为偏微分 方程. 常微分方程 偏微分方程 (本章内容) 分类