
例:从电话公司每月长途电话的帐单中,随机抽取37张,计 算平均费用为33.15元,标准差为21.21元.假定费用服从正 态分布N(4,σ2),σ未知,要检验假设 H0:4=30,H,:4≠30 解:取检验统计量T= x-~t(n-1) S/n 依样本计算检验统计量的值为T,= 33.15-30 =0.90338 21.21 37 41-(n-1)=1-(37-1)=2.03, T≤2.03 说明样本支持原假设,故要接受原假设
例:从电话公司每月长途电话的帐单中, 随机抽取37张, 计 算平均费用为33.15元, 标准差为21.21元. 假定费用服从正 态分布 , 未知, 要检验假设 , N( , ) 2 2 H0 : 30 H1 : 30 S / n X T 解 ~ t( n 1) :取检验统计量 依样本计算检验统计量的值为 0.90338 33.15 30 T 37 21.21 0 说明样本支持原假设,故要接受原假设. 0.05 2 2 1 1 0 t (n 1) t (37 1) 2.03, T 2.03

2.方差σ2的检验 设总体XN(u,o2),X1,X2…,Xn为一组样本, 1)σ的检验(未知) (x检验) 1)提出原假设和备择假设:H0:σ2=o2,H1:σ2≠02 2)选择检验统计量: (n-1)S2 la成立~X(n-) 2=X(n-1) f(x) 3)给定,取 2 2=X2(n-10 0a/2 有P01<22)=1-a 所以,拒绝条件为 x2<X2(n-1) 2 台足或 话母成 否定域 或x2>X2(n-1)
接受域 2) 选择检验统计量: 1) 提出原假设和备择假设: 3) 给定α,取 H0 : σ2 = σ0 2 ; H1 : σ2 ≠ σ0 2 | 0成立 ( 1) 2 0 2 2 H n S ~ (n 1) 2 2 1 2 2 2 1 2 ( 1) ( 1) n n X f(x) α/2 α/2 λ1 λ2 否定域 否定域 设总体X~N(μ,σ2), X1 ,X2 ,…,Xn为一组样本, (1) σ2的检验( μ未知) ( ) 2检验 有P(λ1< <λ2)=1-α 2 所以,拒绝条件为 2 2 2 2 2 1 2 ( 1) ( 1) n n 或 2. 方差σ2的检验

例:在正常的生产条件下,某产品的测试指标 总体XN(o,02),其中o0=023.后来改变生产工艺,出了新产 品,假设新产品的测试指标总体仍为X,且X~N(μ,σ2).从新产 品中随机地抽取10件,测得样本值为x1,x2,…,x10,计算得到 样本标准差S=0.33.试在检验水平=0.05的情况下检验:方 差σ2有没有显著变化? 解建立假设 H:o2=o=0.232,H:o≠o 新产品指标的方差与正常情况下产品指标的方差比较没有 显著变化 21=X2(n-1)=2.7 (10-1)0.33 ≈18.53 2 0.232 2=Xn-1)=19.023 2.7<18.53<19.023,接受H:σ2=o=0.23
例:在正常的生产条件下, 某产品的测试指标 总体X~N(μ0 ,σ0 2),其中σ0=0.23.后来改变生产工艺,出了新产 品,假设新产品的测试指标总体仍为X,且X~N(μ,σ2). 从新产 品中随机地抽取10件, 测得样本值为x1 ,x2 ,…,x10 ,计算得到 样本标准差S=0.33. 试在检验水平α=0.05的情况下检验: 方 差σ2有没有显著变化? 解 建立假设 : 0.23 , 2 2 0 2 H0 2 0 2 1 H : 新产品指标的方差与正常情况下产品指标的方差比较没有 显著变化 . 2 1 2 2 2 1 2 ( 1) 2.7 ( 1) 19.023 n n 18.53 0.23 ( 1) (10 1)0.33 2 2 2 0 2 2 n S 2.7<18.53<19.023,接受 2 2 0 2 0 H : 0.23
P(Z>Z1-a)<a (x) Φ(21-g)=1-a :Z1-u X ◆ 安受成 否定成或 单侧(右侧)统计检验 原假设的确定一般应遵循以下原则 要把等号放在原假设里
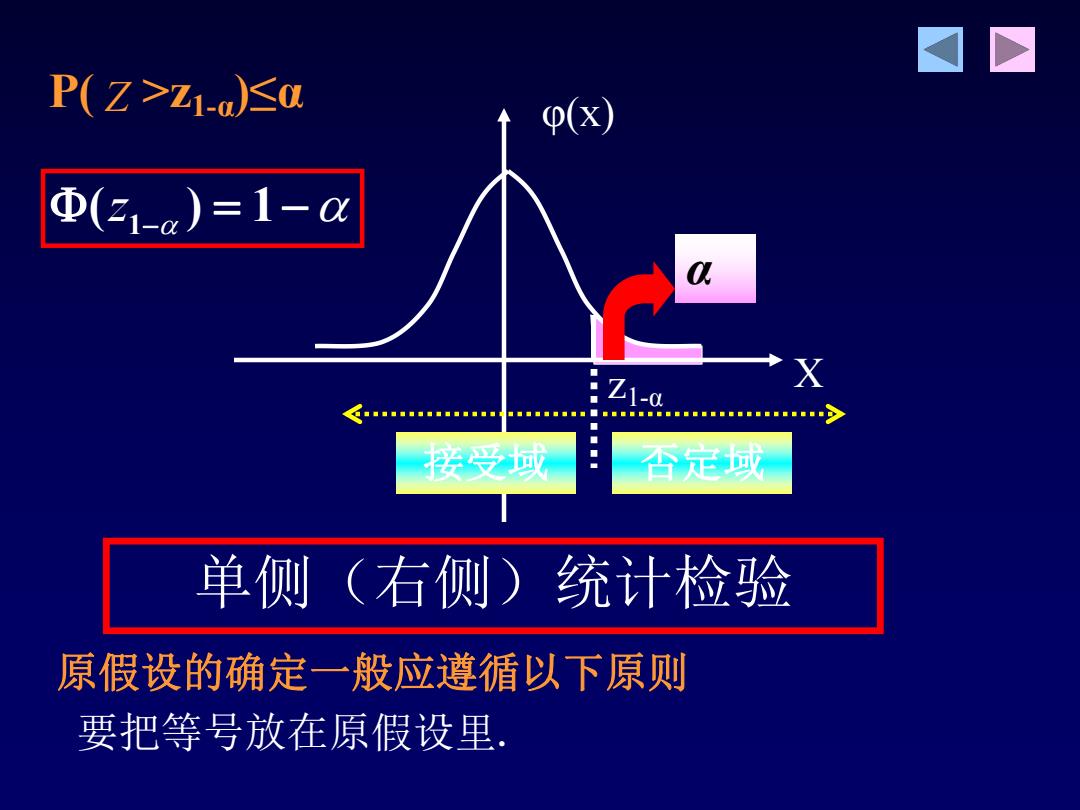
α X φ(x) 接受域 否定域 z1-α 单侧(右侧)统计检验 1 (z ) 1 P( >z1-α Z )≤α 原假设的确定一般应遵循以下原则 要把等号放在原假设里

设总体XN(u,o2),X1,X2…,Xn为一组样本, Ho:μ≤o(已知);H1>o 1)提出原假设和备择假设:H0so,HP>o, 2)对统计量:Z= X-Ho 在H下有 X-丛X-丹 olvn o/√n/√n 对给定的a有 治 所以 P名小n- 3)故拒绝条件为Z>Z1a,其中, Φ3-a)=1-a
2) 对统计量: 设总体X~N(μ,σ2), X1 ,X2 ,…,Xn为一组样本, 1 (z ) 1 . 1) 提出原假设和备择假设: H0 :μ≤μ0 ; H1 :μ>μ0 , 3) 故 拒绝条件为Z> z1-α ,其中, n X Z / 0 对给定的α有 在H0下有 , / / 0 n X n X 0 1 1 { } { } / / X X z z n n 所以 0 1 1 ( ) ( ) / / X X P z P z n n ② H0:μ≤μ0(已知); H1:μ>μ0