
弃真 ≤OX 3.两类错误 取伪 根据小概率原理否定原假设,有可能把本来客观上正确的 假设否定了,造成犯“弃真”的错误,称为第一类错误, Q就是犯第一类错误的概率的最大允许值 另一方面,当原假设不成立时,却作出接受原假设的结论, 造成犯“取伪”的错误,称为第二类错误, 般用B表示犯第二类错误的概率。 当样本容量n一定时,小,B就大,反之,B外,C就大 另外,一般a+B≠1 注意: 增大样本容量n时,可以使a和B同时减小
另一方面,当原假设不成立时,却作出接受原假设的结论, 造成犯“取伪”的错误,称为第二类错误, 就是犯第一类错误的概率的最大允许值. 一般用 表示犯第二类错误的概率. 根据小概率原理否定原假设,有可能把本来客观上正确的 假设否定了,造成犯“弃真”的错误,称为第一类错误, 弃真 取伪 当样本容量n 一定时,小, 就大,反之,小, 就大. 另外,一般 1 3.两类错误 注意: 增大样本容量n时,可以使α和β同时减小

单正态总体的统计检验 设总体XN(以,o2),X1,X2,…,Xn为一组样本, 1.期望的检验 (1)总体方差σ已知时 ①H:μ=o(已知);H1μ≠0 1)提出原假设和备择假设: H0μ=0,H1呋0 2)确定检验统计量:Z= ~N(0,1) 3)对给定a,由原假设成立时P(Z>z12=a得 拒绝条件为ZPZ12,其中, (Z)=1- 2
2) 确定检验统计量: | 0成立 / 0 H n X Z ~ N(0,1) 设总体X~N(μ,σ2), X1 ,X2 ,…,Xn为一组样本, (1) 总体方差σ2已知时 1 2 ( ) 1 . 2 Z ① H0:μ=μ0(已知); H1:μ≠μ0 1) 提出原假设和备择假设: H0 :μ=μ0 ; H1 :μ≠μ0 , 3) 对给定α,由原假设成立时P(|Z|> z1-α/2)=α得 拒绝条件为|Z|> z1-α/2 ,其中, 1.期望的检验 单正态总体的统计检验

p(x) P(ZPz1-a2戶a Z检验 /2 0W2 Z1-2 X 否定成或 ◆ 安受或 否足成或 双侧统计检验
α/2 α/2 X φ(x) 接受域 P(|Z|>z1-α/2)=α 否定域 否定域 z1-α/2 - z1-α/2 双侧统计检验 Z检验

例:用精确方法测量某化工厂排放的气体中有害气体含量 服从正态分布N(23,22),现用一简便方法测量6次得一组数据 23,21,19,24,18,18(单位:十万分之一),若用简便方法测得有害气体含量 的方差不变,问用该方法测得有害气体含量的均值是否有系统偏差? 分析用简便方法测得有害气体含量X~N(u,22), 基本检验H0:=023, 备择检验H1:呋023, 若H成立,则 =-N(0.1) 若取a=0.05,则P{Z>z1-2}=a,即:P{IZP1.96=0.05 在假设成立的条件下,Z>1.96为概率很小事件,一般认为: 小概率事件在一次实验中是不会发生的, 将样本观测值代入Z得Z=X-23=306Z196 小概率事件在一次实验中发生了,故假设不合情理
例:用精确方法测量某化工厂排放的气体中有害气体含量 服从正态分布N(23,22),现用一简便方法测量6次得一组数据 23,21,19,24,18,18(单位:十万分之一),若用简便方法测得有害气体含量 的方差不变,问用该方法测得有害气体含量的均值是否有系统偏差? 分析 用简便方法测得有害气体含量X~N(μ,2 2), 若H0成立,则 ~ (0,1) / 0 N n X Z 若取α=0.05,则 P{|Z|>z1-α/2}=a, 即: P{|Z|>1.96}=0.05, 在假设成立的条件下,|Z|>1.96为概率很小事件,一般认为: 小概率事件在一次实验中是不会发生的, 将样本观测值代入Z得 3.06, 2/ 23 n X Z |Z|>1.96, 基本检验H0 : μ=μ0=23; 备择检验H1 : μ≠ μ0= 23; 小概率事件在一次实验中发生了,故假设不合情理, 即:否定原假设,简便方法测得均值有系统偏差
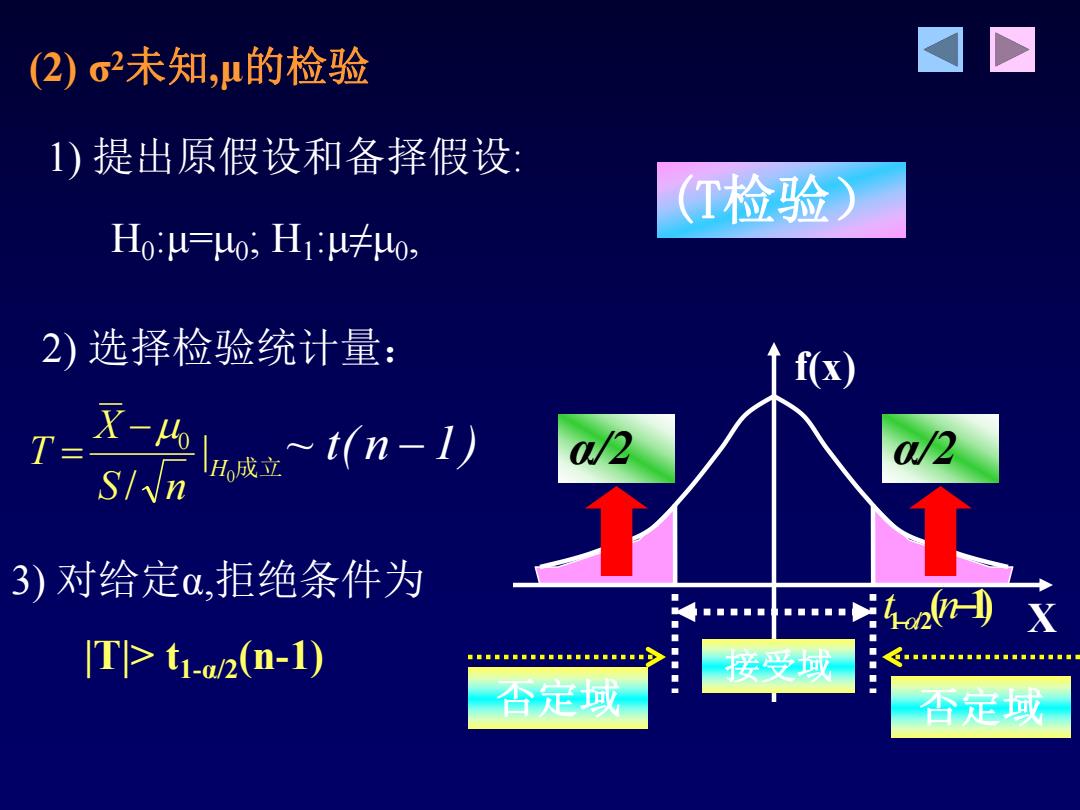
(2)σ未知,n的检验 1)提出原假设和备择假设: (T检验) H0u=0,H1味0, 2)选择检验统计量: ↑fx) T= X /2 a/2 S/√n la成~t(n-l) 3)对给定,拒绝条件为 ■■■■ …n0HX T>t1-a2(n-1) 受或 否足或 否定或
2) 选择检验统计量: 1) 提出原假设和备择假设: H0 :μ=μ0 ; H1 :μ≠μ0 , 3) 对给定α,拒绝条件为 |T|> t1-α/2(n-1) | 0成立 / 0 H S n X T ~ t( n 1) 1 /2 t (n 1) X f(x) α/2 α/2 接受域 否定域 否定域 (T检验) (2) σ2未知,μ的检验