
③ Ho:≥o(已知);H1μ<0 1)提出原假设和备择假设:H2o,H1μ<o 2)选择统计量: Z= X-4 o/√n 3)对给定,否定域为Z<-Z1a 其中 Φz-a)=1-c
2) 选择统计量: 1 (z ) 1 . 1) 提出原假设和备择假设: H0 :μ≥μ0 ; H1 :μ<μ0 , 3) 对给定α, 否定域为Z<- z1-α , 其中 n X Z / 0 ③ H0:μ≥μ0(已知); H1:μ<μ0
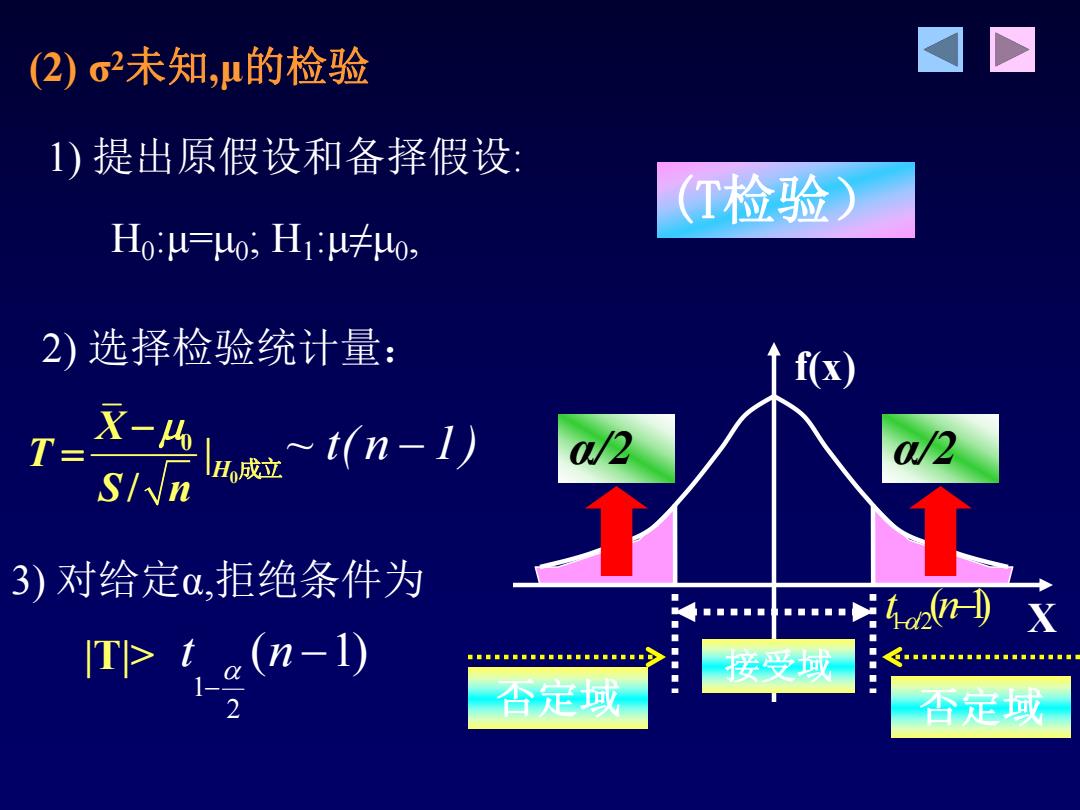
(2)σ未知,n的检验 1)提出原假设和备择假设: (T检验) H0u=0,H1味0, 2)选择检验统计量: ↑fx) TE X一4 a/2 a/2 SIn ms:(n1) 3)对给定,拒绝条件为 ■■■■■ …4n)X ITP t &(n-1) 受成 否足或 否定或
2) 选择检验统计量: 1) 提出原假设和备择假设: H0 :μ=μ0 ; H1 :μ≠μ0 , 3) 对给定α,拒绝条件为 |T|> 0 0 | / H X T S n 成立 ~ t( n 1) 1 /2 t (n 1) X f(x) α/2 α/2 接受域 否定域 否定域 (T检验) (2) σ2未知,μ的检验 1 2 t (n 1)

类似可得: σ2未知,期望的单侧统计检验 统计检验H:μso,H1:心的拒绝条件为 T>t-a(n-1) 统计检验H:2o,H:H<o的拒绝条件为 T<-t-a(n-1)
类似可得: σ2未知,期望的单侧统计检验 H0 :μ≤μ0 ; H1 统计检验 :μ>μ0的拒绝条件为 H0 :μ≥μ0 ; H1 统计检验 :μ<μ0的拒绝条件为 1 T t (n 1) 1 T t (n 1)
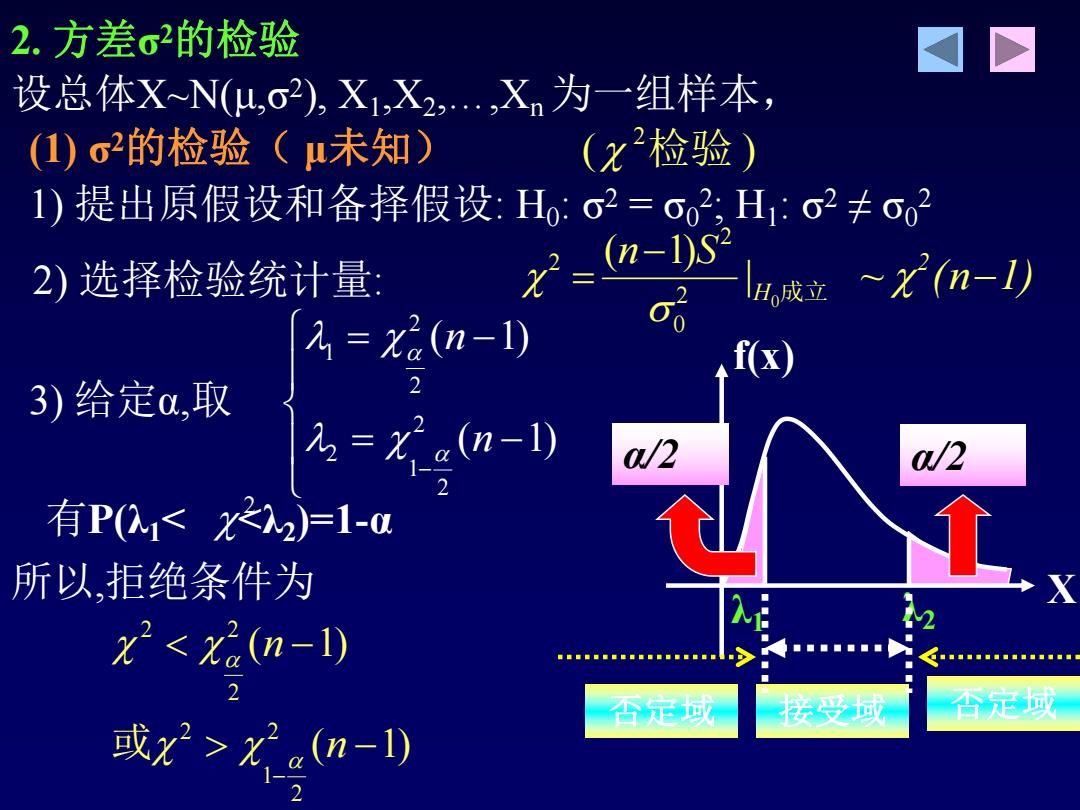
2.方差σ2的检验 设总体XN(u,o2),X1,X2…,Xn为一组样本, (1)σ的检验(未知) (x检验) 1)提出原假设和备择假设:H,:o2=o2,H1:σ2≠o2 2)选择检验统计量: la成立~X(n-) 2=X2(n-1) f(x) 3)给定α,取 2 =X22n-1) a/2 0a/2 有P01<x22=1-u 所以,拒绝条件为 x2<x2(n-1) 2 台元或 话母成 否行域 或x>xX(n-1)
接受域 2) 选择检验统计量: 1) 提出原假设和备择假设: 3) 给定α,取 H0 : σ2 = σ0 2 ; H1 : σ2 ≠ σ0 2 | 0成立 ( 1) 2 0 2 2 H n S ~ (n 1) 2 2 1 2 2 2 1 2 ( 1) ( 1) n n X f(x) α/2 α/2 λ1 λ2 否定域 否定域 设总体X~N(μ,σ2), X1 ,X2 ,…,Xn为一组样本, (1) σ2的检验( μ未知) ( ) 2检验 有P(λ1< <λ2)=1-α 2 所以,拒绝条件为 2 2 2 2 2 1 2 ( 1) ( 1) n n 或 2. 方差σ2的检验

总体期望未知时,σ的单侧假设检验 1)提出原假设和备择假设:H:σ2≤o2;H1:2>o2 2)选择统计量X=n-1S 则在H,下 (u-)s -)s -in-1) 2 对含定a有“2>元m》=0心云.-w 脚把xa-小公w小 3)所以,拒绝条件为 x2>2(n-1)
1) 提出原假设和备择假设: H0: σ2 ≤σ0 2; H1: σ2 >σ0 2 2 2 2 2 0 (n 1)S (n 1)S ~ (n 1) 2 2) 选择统计量 2 2 2 0 (n 1)S 则在H0下 对给定的α,有 即 3) 所以,拒绝条件为 2 2 1 (n 1) 2 2 2 2 2 1 2 1 0 ( 1) ( 1) { ( 1)} { ( 1)} n S n S n n 2 2 2 2 2 1 2 1 0 ( 1) ( 1) ( 1) ( 1) n S n S P n P n 总体期望μ未知时,σ2的单侧假设检验