《线性代数》课程教学资源（PPT课件，A）4-2齐次线性方程组

第四章线性方程组二、基础解系及其求法如果方程组（4-5）有非零解，它一定有无穷多非零解1、基础解系设5,52…,5,是方程组（4-5）的一组解向量，若满足：1)线性无关；2)方程组的任意解向量都能由1,2.,5,线性表示；则称1,52,5,是方程组的基础解系

第四章 线性方程组 二、基础解系及其求法 如果方程组(4-5)有非零解，它一定有无穷多非零解. 1、基础解系 1)线性无关； 1 2 , , , - r 设    是方程组（4 5）的一组解向量，若满足：

第四章线性方程组2、存在性及求法定理：如果方程组（4-5)有非零解，它必有基础解系并且基础解系所含向量的个数为n一R(A)证明：设A经过初等行变换可化为：br+nbrr+rn1

第四章 线性方程组 2、存在性及求法 定理：如果方程组(4-5)有非零解，它必有基础解系， 并且基础解系所含向量的个数为 n R A − ( ). 证明： 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I + +               =            

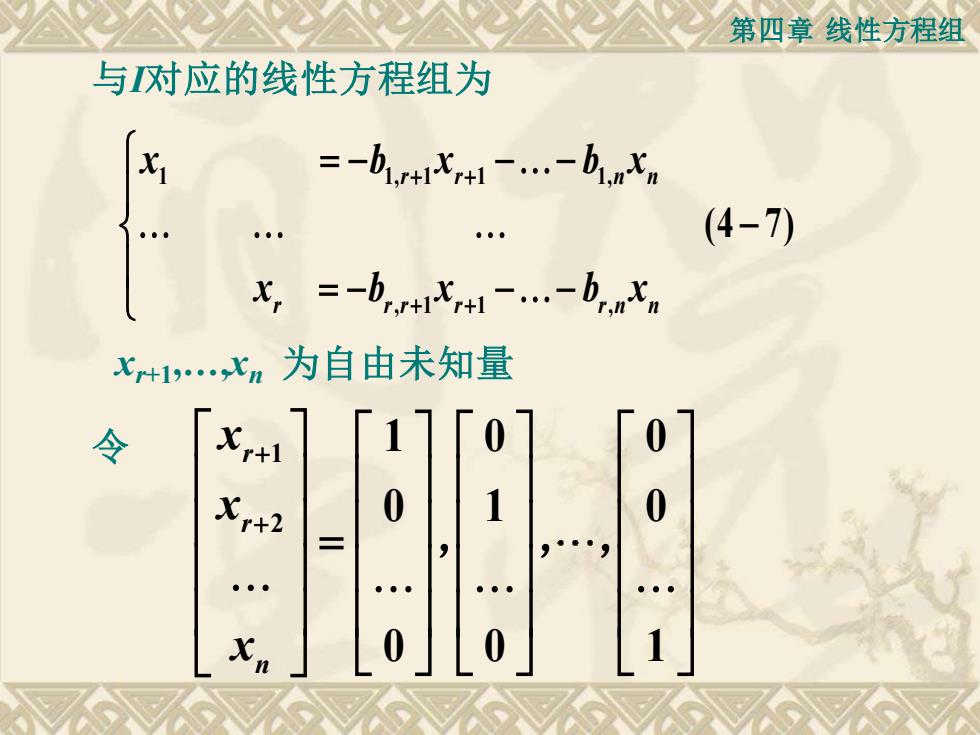
第四章线性方程组与I对应的线性方程组为Xi+1Xr+1 -...-b,1(4-7)=-bx.-bXPr,r+1Xr+1 -.r-nXr+1n为自由未知量x今r+10七r+2

第四章 线性方程组 1 1, 1 1 1, , 1 1 , (4 7) r r n n r r r r r n n x b x b x x b x b x + + + +  = − −−     −  = − −−  与I对应的线性方程组为 xr+1,.,xn 为自由未知量 1 2 1 0 0 0 1 0 0 0 1 r r n x x x + +                   =                                   ， ， ， 令

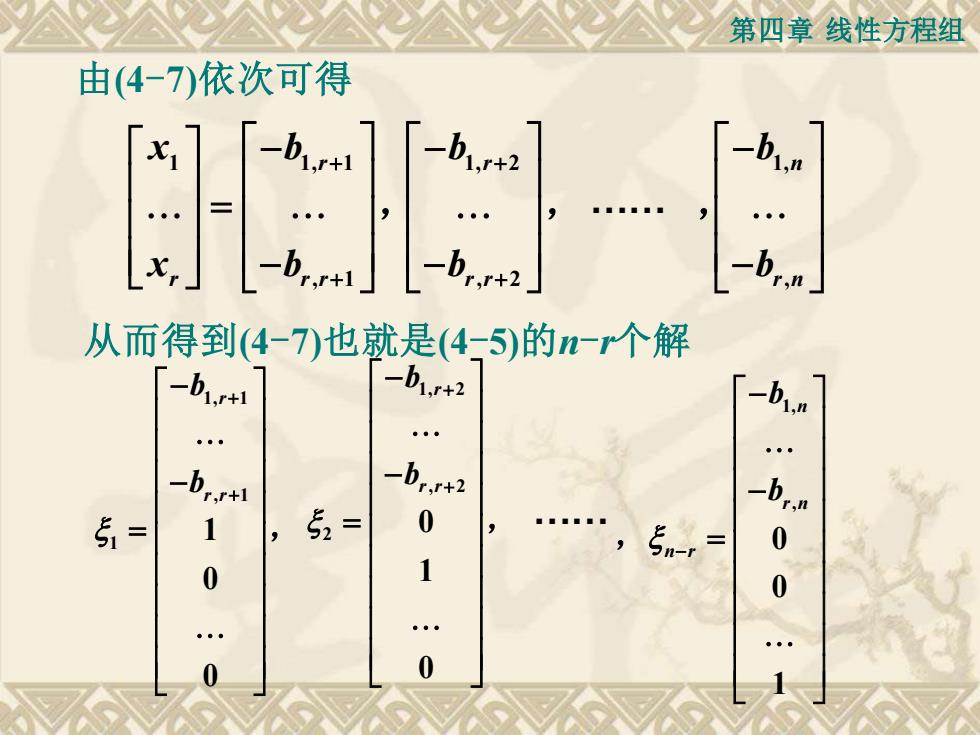
第四章线性方程组由（4-7)依次可得h-hx.1,r+1.r+1r.r+l,r+2从而得到(4-7)也就是(4-5)的n-r个解-b1,r+2-b1,+16-b,r+2-b,r+15 =00

第四章 线性方程组 1 1, 1 , 1 r r r r x b x b + +     −        =          −  ， 1, 2 , 2 r r r b b + +   −        −  ， 1, , n r n b b   −        −  ， 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解 1, 1 , 1 1 1 0 0 r r r b b  + +   −        −   =              ， 1, 2 , 2 2 0 1 0 r r r b b  + +   −        −   =              ， 1, , 0 0 1 n r n n r b b  −   −        −   =              ，