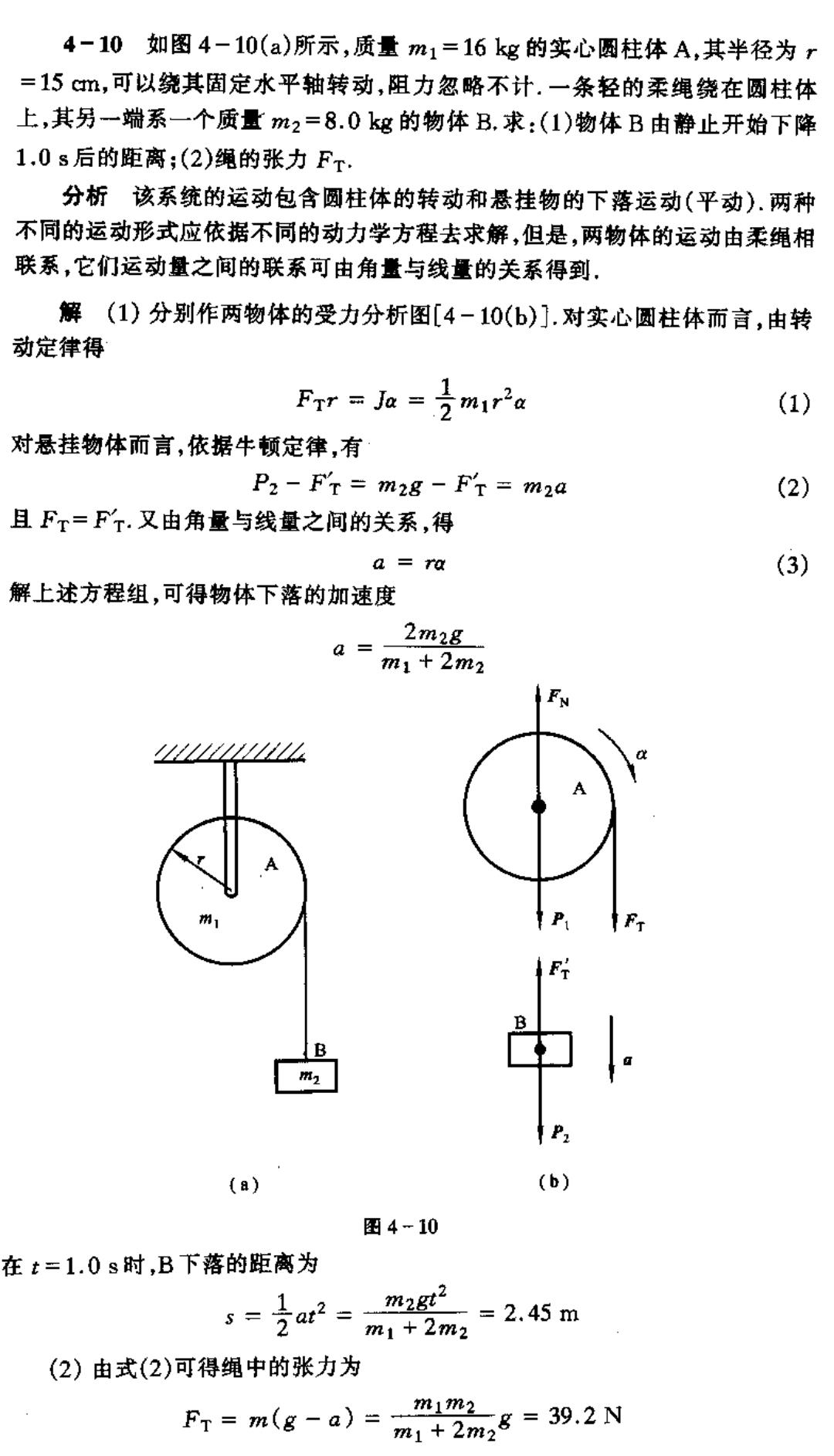
4-10如图4-10(a)所示,质量m1=16kg的实心圈柱体A,其半径为r =15,可以绕其固定水平轴转动,阻力忽略不计.一条轻的柔绳绕在圆柱体 上,其另一端系一个质量m2=8.0kg的物体B.求:(1)物体B由静止开始下降 1.0s后的距离:(2)绳的张力FT. 分析该系统的运动包含圆柱体的转动和悬挂物的下落运动(平动).两种 不同的运动形式应依据不同的动力学方程去求解,但是,两物体的运动由柔绳相 联系,它们运动量之间的联系可由角置与线量的关系得到. 解(1)分别作两物体的受力分析图[4-10(b)].对实心圆柱体而言,由转 动定律得 (1) 对悬挂物体而言,依据牛顿定律,有 P2 FT m28 -FT m2a (2) 且Fr=Fr.又由角量与线量之间的关系,得 a=ra (3) 解上述方程组,可得物体下落的加速度 a= 2m28 m1+2m2 B (a) (b) 图4-10 在t=1.0s时,B下落的距离为 s-ar= agt =2.45m m1+2m2 (2)由式(2)可得绳中的张力为 Ft=m(g-a)=m8=39.2N m1+2m2
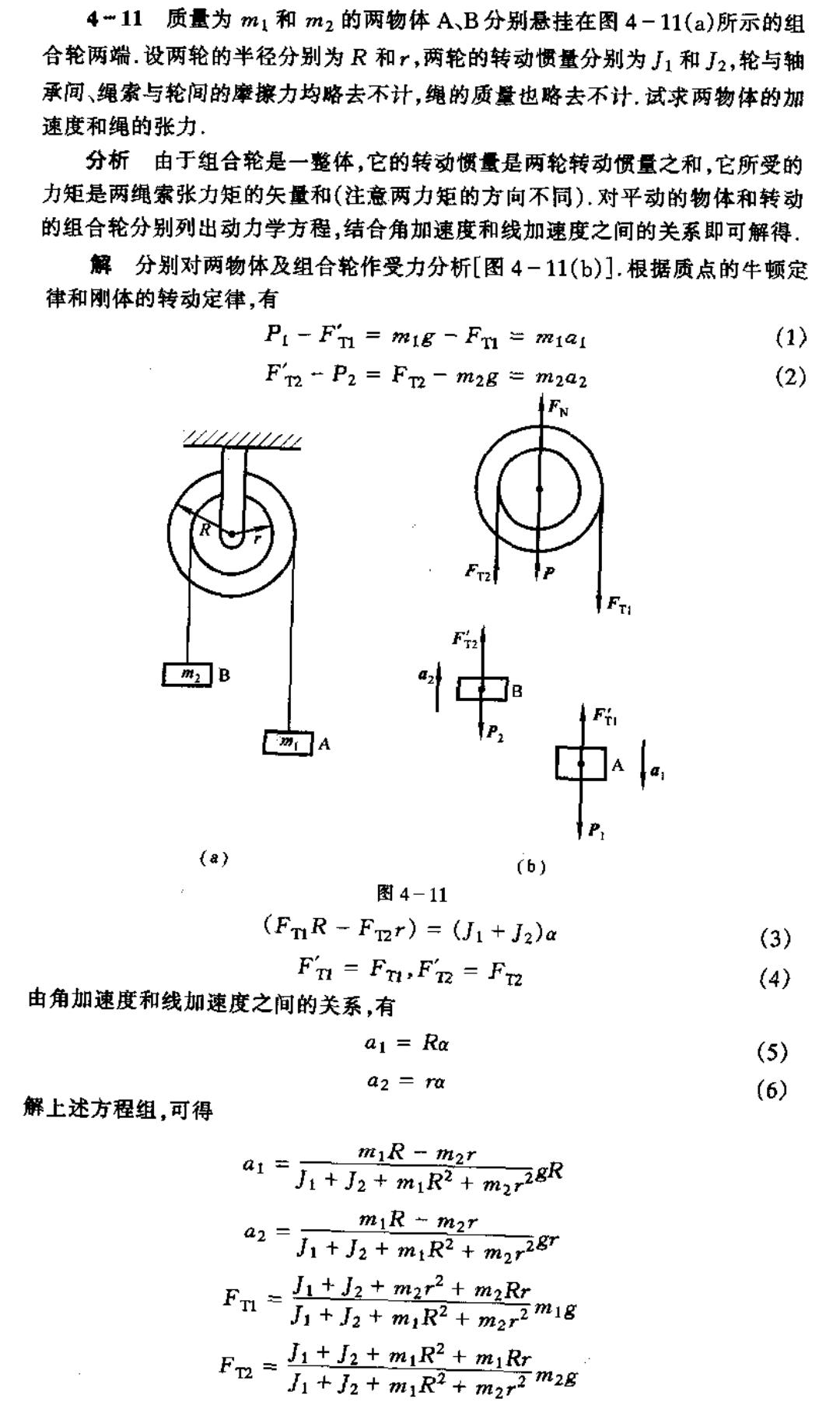
4-11质量为m1和m2的两物体A、B分别悬挂在图4-11(a)所示的组 合轮两端.设两轮的半径分别为R和r,两轮的转动惯量分别为J1和J2,轮与轴 承问、绳索与轮间的摩擦力均略去不计,绳的质量也略去不计.试求两物体的加 速度和绳的张力. 分析由于组合轮是一整体,它的转动惯量是两轮转动惯量之和,它所受的 力矩是两绳索张力矩的矢量和(注意两力矩的方向不同),对平动的物体和转动 的组合轮分别列出动力学方程,结合角加速度和线加速度之间的关系即可解得. 解分别对两物体及组合轮作受力分析[图4一11(b)].根据质点的牛顿定 律和刚体的转动定律,有 P1-F'T =m1g-FT mial (1) F'T2 P2 Fm-m2g m2a2 (2) tttultllits m2 B () 图4-11 (FnR-Fzr)=(Ji+J2)a (3) FT=FT,FT=Ft (4) 由角加速度和线加速度之间的关系,有 a1 Ra (5) a2=ra (6) 解上述方程组,可得 mR m2r a1=人+J2+mR2+m27歌 mR-m2r a2=1+J2+m1R2+m278 Fn+martmaRr 2+mR2+mm1g Fn=++m1R2+m1R +m+m2m2g

4-12如图4一12所示装置,定滑轮的半径为r,绕转轴的转动惯量为J, 滑轮两边分别悬挂质量为m1和m2的物体A、B.A置于倾角为日的斜面上,它 和斜面间的摩擦因数为4.若B向下作加速运动时,求:(1)其下落加速度的大 小:(2)滑轮两边绳子的张力.(设绳的质量及伸长均不计,绳与滑轮间无滑动,滑 轮轴光滑) (b) 图4-12 分析这是连接体的动力学问题,对于这类问题仍采用隔离体的方法,从受 力分析若手,然后列出各物体在不同运动形式下的动力学方程.物体A和B可 视为质点,则运用牛颠定律,由于绳与潜轮间无滑动,滑轮两边绳中的张力是不 同的,滑轮在力矩作用下产生定轴转动,因此,对滑轮必须运用刚体的定轴转动 定律,列出动力学方程,并考忠到角量与线量之间的关系,即能解出结果来。 解作A、B和滑轮的受力分析图4-12(b).其中A是在张力F1、重力 P1,支持力F、和摩擦力F:的作用下运动,根据牛顿定律,沿斜面方向有 FTI-migsin 8-umigoos 0 miat (1) 而B则是在张力F卫和重力P2的作用下运动,有 m2g -FT2 m2a2 (2) 由于绳子不能伸长、绳与轮之间无滑动,则有 al=a2=ra (3) 对滑轮而言,根据定轴转动定律有 Fzr-Fnr±Ja (4) 且有 Fn FT,FR=FT (5) 解上述各方程可得 a1=a2= m28 migsin 6-umigoos 6 m1+m2+名 Fn=m1m,81+m9+4cos0)+(sin日+es0)m1l2 mI m2 Jir2 mim2g(1 +sin 0+ucos )+m2gl/r2 n1+m2+J/r2