
4一5用落体观察法测定飞轮的转动惯蟹,是将半径为R的飞轮支承在O 点上,然后在绕过飞轮的绳子的一端挂一质量为m的重物,令重物以初速度为 零下落,带动飞轮转动(图4一5).记下重物下落的距离和时间,就可算出飞轮的 转动惯量.试写出它的计算式.(假设轴承间无摩擦) 分析在运动过程中,飞轮和重物的运动形 式是不同的.飞轮作定轴转动,而重物是作落体 运动,它们之间有着内在的联系.由于绳子不可 伸长,并且质量可以忽略.这样,飞轮的转动惯 量,就可根据转动定律和牛顿定律联合来确定, 其中重物的加速度,可通过它下落时的匀加速运 动规律来确定 该题也可用功能关系来处理.将飞轮、重物 和地球视为系统,绳子张力作用于飞轮、重物的 图4-5 功之和为零,系统的机械能守恒.利用匀加速运 动的路程、速度和加速度关系,以及线速度和角速度的关系,代人机械能守恒方 星中即可解得. 解1设绳子的拉力为F,对飞轮而言,根据转动定律,有 FTR Ja (1) 而对重物而言,由牛顿定律,有 mg -FT=ma (2) 由于绳子不可伸长,因此,有 a Ra (3) 重物作匀加速下落,则有 h=Tar (4) 由上述各式可解得飞轮的转动惯量为 J=mR2器 -1 解2根据系统的机械能守恒定律,有 -m8gh+m2+号a2=0 (1) 而线速度和角速度的关系为 =Ro (2) 义根据重物作匀加速运动时,有 =at (3) v2=2ah (4) 由上述各式可得 J=mR(器- 若轴承处存在摩擦,上述测量转动惯量的方法仍可采用.这时,只需通过用 两个不同质量的重物做两次测量即可消除摩擦力矩带来的影响

4-6一飞轮由一直径为30cm,厚度为2.0cm的圆盘和两个直径为 10cm,长为8.0cn的共轴圆柱体组成,设飞轮的密度为7.8×103kg"m3,求飞 轮对轴的转动惯量. 分析根据转动惯量的可叠加性,飞轮对轴 的转动惯量可视为圆盘与两圆柱体对同轴的转 动惯量之和;而匀质圆盘、圆柱体对轴的转动惯 量的计算可查书中公式,或根据转动惯量的定 义,用简单的积分计算得到 解根据转动惯量的叠加性,由匀质圆盘、 图4-6 圆柱体对轴的转动惯量公式可得 J=1+五=2×分m(+m(月 =6ro(ad1+3a)=0.136kgm
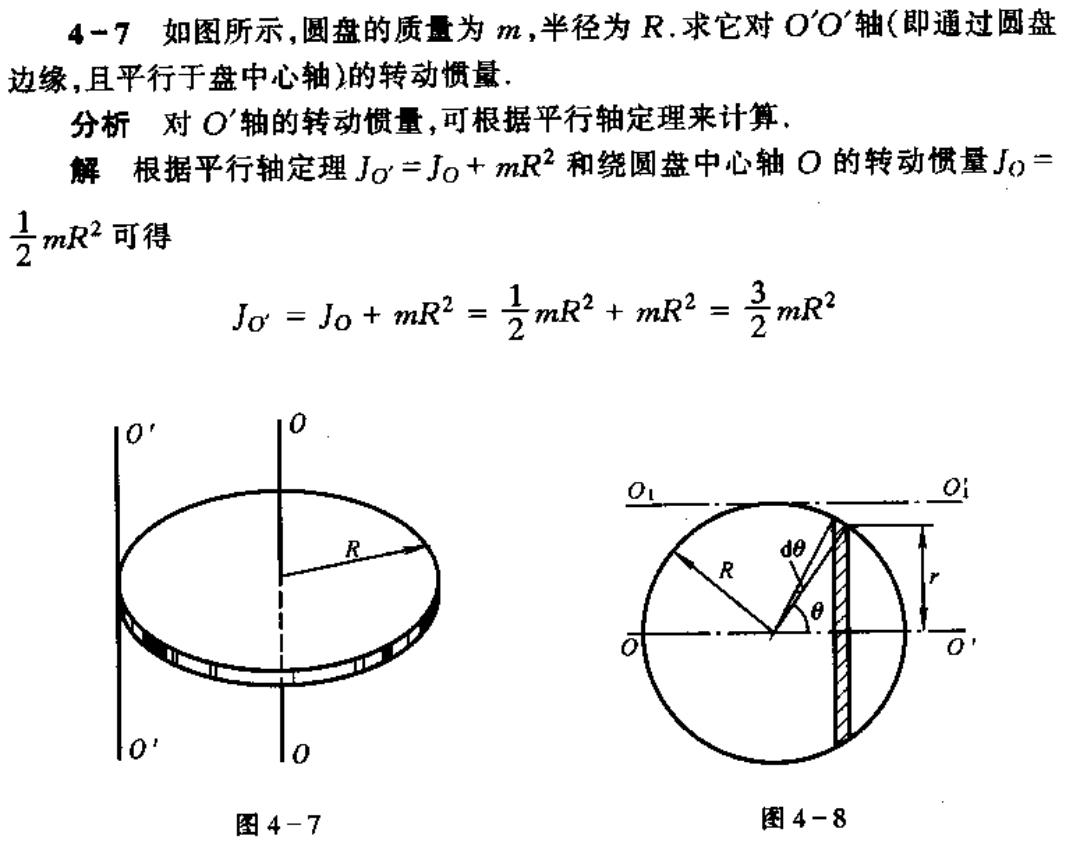
4一7如图所示,圆盘的质量为m,半径为R.求它对OO轴(即通过圆盘 边缘,且平行于盘中心轴的转动惯量. 分析对O轴的转动惯量,可根据平行轴定理来计算, 解根据平行轴定理Jo=J0+mR2和绕圆盘中心轴O的转动惯量Jo= 名mR2可得 Jo Jo+mR2 -mki+m2m 0 图4-7 图4-8

4~8试证明质量为m,半径为R的均匀球体,以直径为转轴的转动惯量 为号mR2,如以和球体相切的线为轴,其转动惯墨又为多少? 分析匀质球体以直径为转轴的转动惯量可视为一系列垂直于转轴的圆盘 组成,这样,在已知圆盘绕其中心轴的转动惯量的基础上,根据转动惯量的叠加 性,采用积分的方法,即可求出球体的转动惯量. 证如图4-8所示,图中阴影部分的小圆盘对O0轴的转动惯量为 d =rdm =(R2-2)p(R2-)dz 式中p=没为匀质球体的密度.则球体以其直径00'为转轴的转动惯量为 J-j小U-2o(R2-2ar=号mR 又由平行轴定理可得球绕O1O轴的转动惯量为 了=J+mR2=子mR2

4一9质量面密度为。的均匀矩形板,试证其对与板面垂直的,通过几何 中心的轴线的转动惯量为员b(2+62).其中1为矩形板的长,b为它的宽。 分析根据转动惯量定义,可直接采用面积 分的方法对匀质矩形板进行计算. 证取如图4-9所示坐标,在板上取一质元 m dm=adxdy,它对与板面垂直的,通过几何中心 b 的轴线的转动惯量为 dI =(z2+y2)adxdy 整个矩形板对该轴的转动惯量为 图4一9 2lb(12+b2)