OA、多元函数的概念7在几何上,U(P,d)表示以P(x.,y)为中心,d为半径的圆的内部(不含圆周),如图9.1所示,04图9.1
图 9.1 一、多元函数的概念 6 O x y P0

0O?0一、多元函数的概念上述邻域U(P.d)去掉中心P(xa,y)后,称为P(xo.y)的去心邻域,记作U(Pd),即U(P,d)= fx, )lo <V(x- xo)* +(y- yo) <d如果不需要强调邻域的半径d,则用U(P)表示点P(xo,Jo)的邻域,用U(P)表示点P(xo.y)的去心邻域
一、多元函数的概念 7

OOA0一、多元函数的概念(2)区域设E是xOy平面上的一个点集,P是xOy平面上的一点,则P与E的关系有如下情形:①内点:如果存在P的某个邻域U(P),使得U(P)iE,则称点P为E的内点,如图9.2所示②边界点:如果在点P的任何邻域内,既有属于E的点,也有不属于E的点,则称点P为E的边界点.E的边界点的集合称为E的边界,如图9.3所示,图9.2图9.3
(2)区域 图 9.2 一、多元函数的概念 8 P E E P 图 9.3

A一、多元函数的概念③开集:如果点集E的每一点都是E的内点,则称E为开集④连通集:设E是平面点集,如果对于E中的任何两点,都可用完全含于E的折线连接起来,则称E是连通集③开区域:连通的开集称为开区域,也称区域6闭区域:开区域连同它的边界称为闭区域?
一、多元函数的概念 9
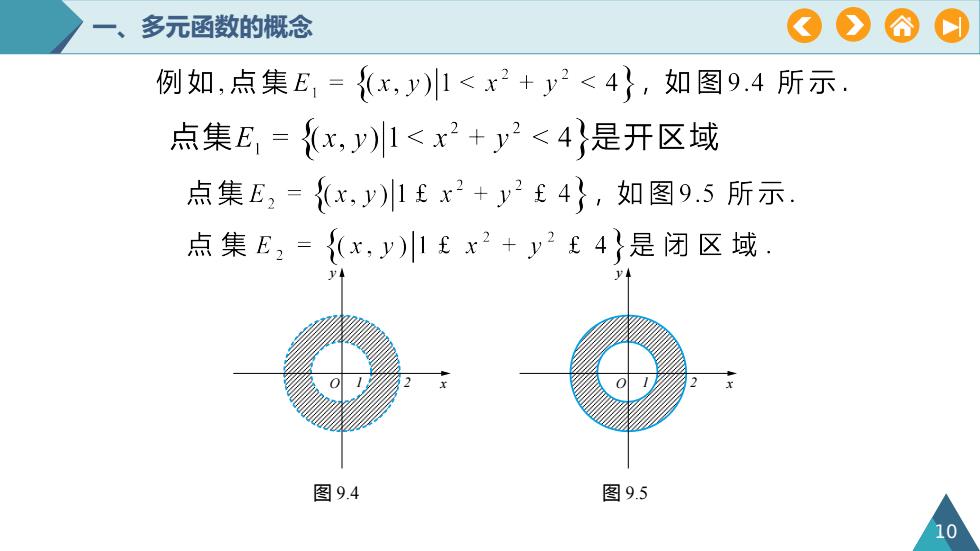
O#A一、多元函数的概念例如,点集E,=(x,)1x2+2<4,如图9.4所示,点集E,=(x,)1x2+2<4是开区域点集E=(x)1x2+4,如图9.5所示点集=()+24是闭区域.图9.4图9.5
图 9.4 一、多元函数的概念 10 O 1 2 y x O 1 2 y x 图 9.5