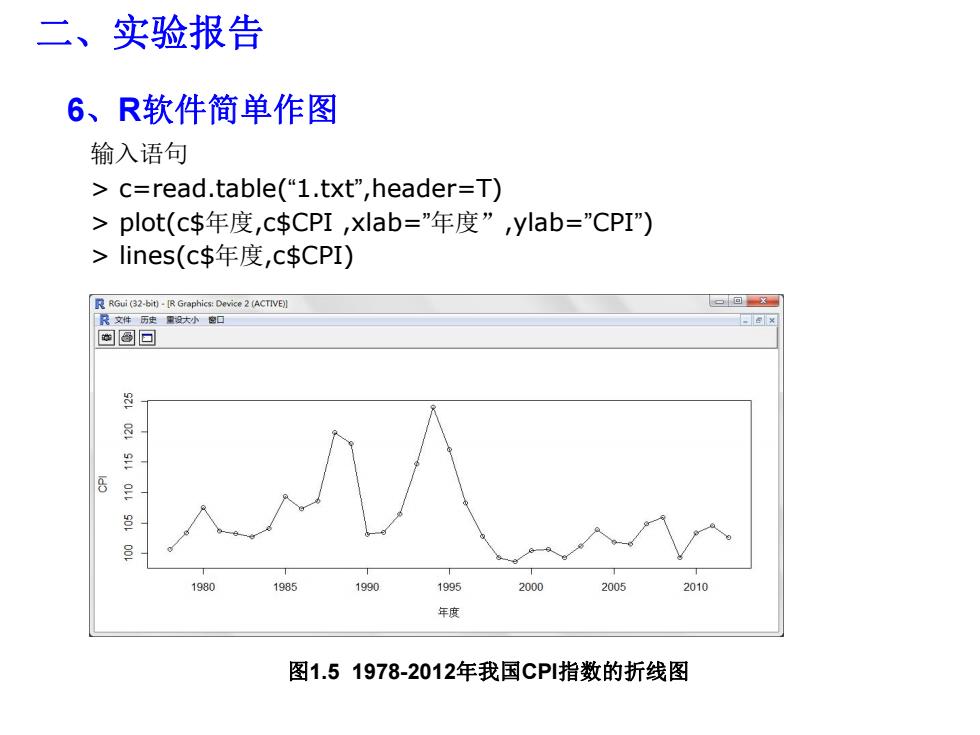
二、实验报告 6、R软件简单作图 输入语句 c=read.table("1.txt",header=T) >plot(c$年度,c$CPI,Xlab="年度”,ylab=”CPI") >lines(c$年度,c$CPI) RGui(32-bit)-[R Graphics:Device 2 (ACTIVE)] 回× 表文件历使需设大小险口 海图回 e 1980 1985 1990 1995 2000 2005 2010 年度 图1.51978-2012年我国CP1指数的折线图
二、实验报告 6、R软件简单作图 输入语句 > c=read.table(“1.txt”,header=T) > plot(c$年度,c$CPI ,xlab=”年度” ,ylab=”CPI”) > lines(c$年度,c$CPI) 图1.5 1978-2012年我国CPI指数的折线图

二、实验报告 6、R软件简单作图 运用简单的R编程,得到关于GDP与CPI的双折线图语句如下: cl=read.csv("1.csv",header=T) X<-cl$年度 y<-cl$GDP plot(x,y,type="",main="折线图",xlab="年度 ",ylab="GDPCPI",xlim=c(1978,2012),ylim=c(95,125)) y2<-cl$CPI points(x,y2,type="I",col="red")
运用简单的R编程,得到关于GDP与CPI的双折线图语句如下: cl=read.csv("1.csv" ,header=T) x<-cl$年度 y<-cl$GDP plot(x,y,type= "l" ,main= "折线图" ,xlab= "年度 " ,ylab= "GDP或CPI" ,xlim=c(1978,2012),ylim=c(95,125)) y2<-cl$CPI points(x,y2,type= "l" ,col= "red") 6、R软件简单作图 二、实验报告
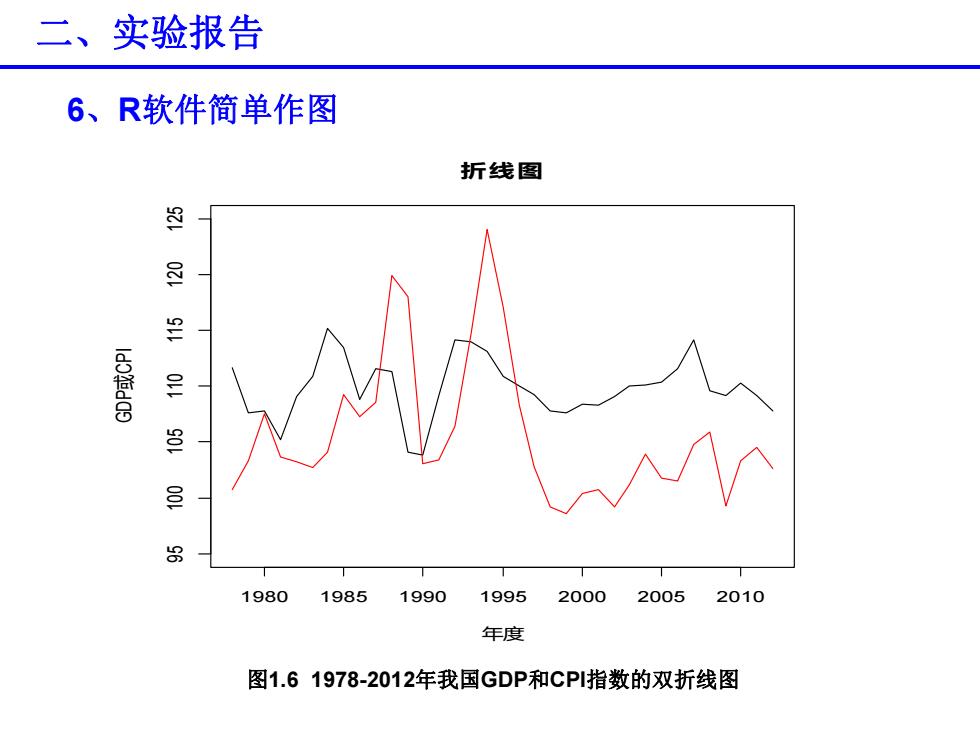
二、实验报告 6、R软件简单作图 折线图 超 8 1980198519901995200020052010 年度 图1.61978-2012年我国GDP和CPI指数的双折线图
6、R软件简单作图 二、实验报告 1980 1985 1990 1995 2000 2005 2010 9 5 10 0 10 5 110 115 12 0 12 5 折线图 年度 G D P 或 C PI 图1.6 1978-2012年我国GDP和CPI指数的双折线图

二、实验报告 6、R软件简单作图 输入语句 plot(c$GDP,c$CPI,xlab="GDP",ylab="CPI") RGui(32-bit)-[R Graphics:Device 2 (ACTTVE)] 回x 民文件历史里设大小金口 匈圆回 是 是 。0 104 106 108 110 112 114 GDP 图1.71978-2012年我国GDP和CPI指数的散点图
二、实验报告 6、R软件简单作图 输入语句 > plot(c$GDP,c$CPI,xlab= "GDP" ,ylab= "CPI") 图1.7 1978-2012年我国GDP和CPI指数的散点图

二、实验报告 7、描述性统计分析 data_outline <-function(x){ n <-length(x) m <-mean(x) 输入语句 v<-var(x) s <-sd(x) 对GDP和CPI me<-median(x) 进行描述性统计分析 cv<-100*s/m css <-sum((x-m)^2) uss <-sum(x^2) R <-max(x)-min(x) R1 <-quantile(x,3/4)-quantile(x,1/4) sm <-s/sqrt(n) g1<-n/(n-1)*(n-2)*sum(x-m)^3)/s^3 g2<-(n*(n+1)/(n-1)*(n-2)*(n-3)*sum(x-m)^4)/s^4 (3*(n-1)^2/(n-2)*(n-3)) data.frame(N=n,Mean=m,Var=v,Std_dev=s,Median=me,std_ mean=sm,CV=cV, CSS=css,USS=uss,R=R,R1=R1,Skewness=g1,Kurtosis=g2,ro w.names=1) c <-read.table("1.txt",header=T) x1<-data_outline(c$GDP) x2<-data_outline(c$CPI) X1 x2
二、实验报告 7、描述性统计分析 输入语句 对GDP和CPI 进行描述性统计分析 data_outline <- function(x){ n <- length(x) m <- mean(x) v <- var(x) s <- sd(x) me <- median(x) cv <- 100*s/m css <- sum((x-m)^2) uss <- sum(x^2) R <- max(x)-min(x) R1 <- quantile(x,3/4)-quantile(x,1/4) sm <- s/sqrt(n) g1 <- n/((n-1)*(n-2))*sum((x-m)^3)/s^3 g2 <- ((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)^4)/s^4 - (3*(n-1)^2/((n-2)*(n-3)))) data.frame(N=n,Mean=m,Var=v,Std_dev=s,Median=me,std_ mean=sm,CV=cv, CSS=css,USS=uss,R=R,R1=R1,Skewness=g1,Kurtosis=g2,ro w.names=1) } c <- read.table("1.txt",header=T) c x1<-data_outline(c$GDP) x2<-data_outline(c$CPI) X1 x2