
3.电容元件VCR的相量形式 时域形式: 已知(t)=V2Ucos(ot+) ie()=C=-oCUsinot+) dt =N2 @CUcs((@t+g.+2》 相量形式: U=U∠Ym ic=oCU∠平n+π/2)=joCU∠Ψ 相量关系: 相量模型 有效值关系: 相应关系:罗=平
时域形式: 相量形式: ( ) 2 cos( ) Ψu 已知 u t = U t + ) 2 2 cos( 2 sin( ) d d ( ) ( ) π = + + = = − + u C u CU t Ψ CU t Ψ t u t i t C 则 相量模型 iC(t) u(t) C + - • U I C • + - jωC 1 相量关系: I j X I C j I j C U C = = − = − 1 3. 电容元件VCR的相量形式 ( 2) C u u u I CU Ψ j CU Ψ U U Ψ = + = = • • 有效值关系: 相位关系:i=u+90° I C U 1 =
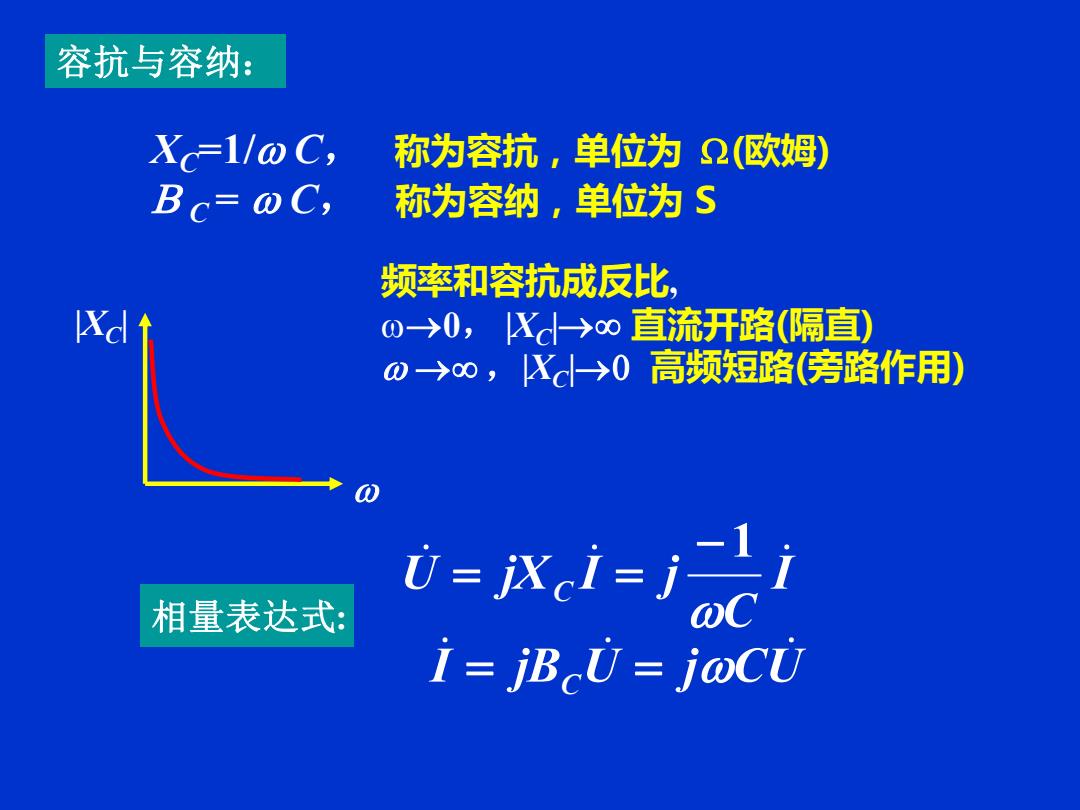
容抗与容纳: Xc=1/@C, 称为容抗,单位为①欧姆) Bc=@C, 称为容纳,单位为5 频率和容抗成反比, Xc↑ 0→0,Xc→o直流开路(隔直) w-→∞,X→0高频短路(旁路作用) 相量表达式: C=1-成 i=jBcU=jaCU
XC=1/ C, 称为容抗,单位为 (欧姆) B C = C, 称为容纳,单位为 S 频率和容抗成反比, →0, |XC |→ 直流开路(隔直) → ,|XC|→0 高频短路(旁路作用) |XC | 容抗与容纳: 相量表达式: I jB U j CU I C U jX I j C C = = − = = 1
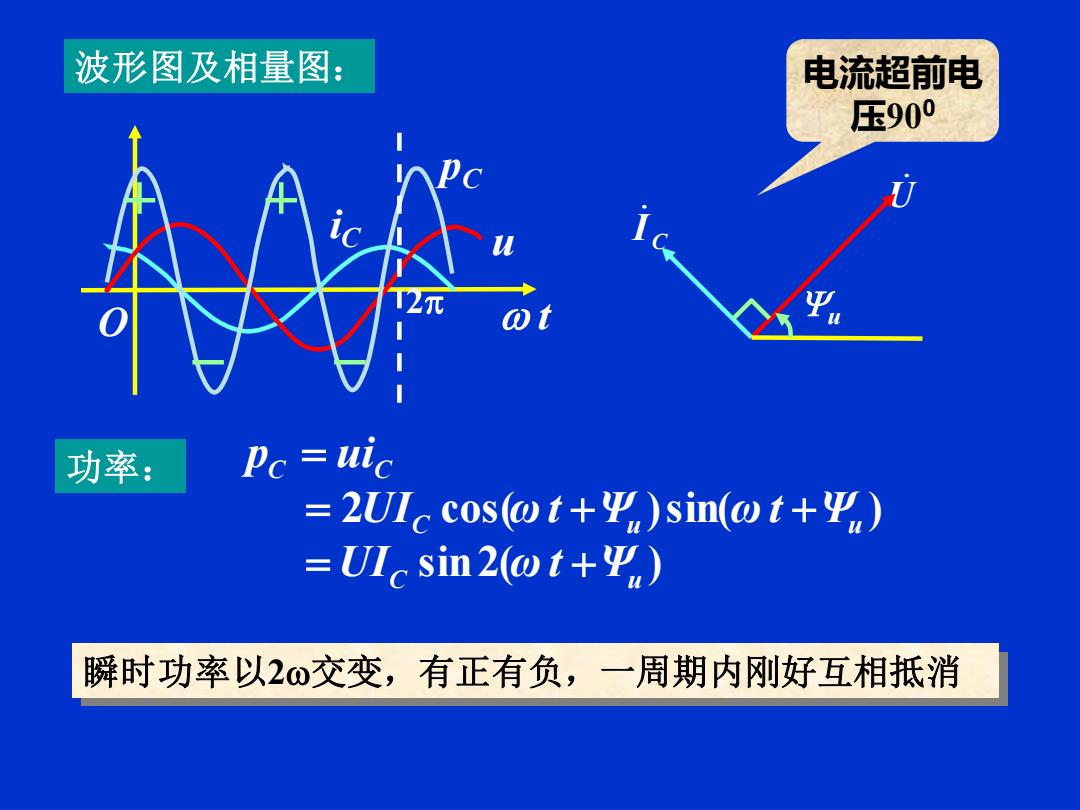
波形图及相量图: 电流超前电 压900 功率: Pc uic =2 I cos(@t+平)sin(wt+Ψa) =UIc sin2(ωt+平) 瞬时功率以2o交变,有正有负,一周期内刚好互相抵消
功率: sin2( ) 2 cos( )sin( ) C u C u u C C UI ω t Ψ UI ω t Ψ ω t Ψ p ui = + = + + = t iC O u pC 2 瞬时功率以2交变,有正有负,一周期内刚好互相抵消 U C I u 波形图及相量图: 电流超前电 压900

4.基尔霍夫定律的相量形式 同频率的正弦量加减可以用对应的相量形式来进行 计算。因此,在正弦电流电路中,KC和KVL可用相应 的相量形式表示: ∑)=0→∑ie)=∑Re2[i+,+…}o=0 ◆∑i=0 ∑4()=0→ ∑0=0 上式表明:流入某一节点的所有正弦电流用相量表 示时仍满足KCL;而任一回路所有支路正弦电压用相量 表示时仍满足KVL
4. 基尔霍夫定律的相量形式 i(t) = 0 同频率的正弦量加减可以用对应的相量形式来进行 计算。因此,在正弦电流电路中,KCL和KVL可用相应 的相量形式表示: 上式表明:流入某一节点的所有正弦电流用相量表 示时仍满足KCL;而任一回路所有支路正弦电压用相量 表示时仍满足KVL。 ( ) = Re 2 + + = 0 1 2 j t i t I I e I = 0 u(t) = 0 U = 0