
《线性代数C》课程教学大纲 一、课程基本信息 课程名称 线性代数C Linear Algebra C 课程编号 L12021 适用专业理工、经管类相关专业 课性质 公业课 兰学时 32学时学分 )学分 理论学时 32学时 实验学时0学时实践学时0学时开课学期第2学期 先修课程高等数学 后续课程 短阵分析、数值计算、电路分析、信号处理、测量学、计算机图形学、计算机 辅助设计、密码学等 二、课程性质和课程目标 1.课程性质 线性代数起源于线性方程组的解法,是19世纪后期发展起来的一个数学分支,是理 工科专业和经管类专业的一门重要数学基础课,也是硕士研究生入学考试数学科目中的 部分。通过本课程的学习使学生了解和掌握行列式、矩阵、线性方程组等基本理论和基本 知识,并具有熟练的矩阵运算能力及用矩阵方法解决一些实际问题的能力,提高学生的抽 象思维能力、逻辑推理能力、实际应用能力以及解题的技能与技巧。 2.课程目标 课程目标1:理解行列式及余子式、代数余子式的概念,掌握行列式的展开法则:掌 握行列式的基本性质及常见的几种计算行列式的方法:掌握克莱姆法则。 课程目标2:理解维向量及向量组线性相关、线性无关的概念:掌握向量的线性关 系与线性方程组的联系;掌握判断向量组线性相关及无关的方法:理解最大线性无关组与 向量组秩的概念:会利用矩阵的初等变换求最大线性无关组及矩阵的秩。 课程目标3:掌握矩阵的基本运算;掌握逆矩阵的概念及其存在的充分必要条件;理 解矩阵的初等变换规则,并会用初等变换法求矩阵的逆:掌握矩阵分块的概念及分块矩阵 的运算规则。 课程目标4:理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解 的充分必要条件:理解齐次线性方程组的基础解系及通解等概念:理解非齐次线性方程组 的解的结构及通解等概念:掌握用初等行变换求线性方程组通解的方法。 课程目标5:通过线性代数课程的学习,使学生具有较强的线性运算能力、抽象思维 能力、逻辑推理能力、空间想象能力和自学能力等:培养和提高学生运用数学方法分析问 题和解决问题(包括解决实际问题)的意识和能力:使学生获得各专业所需的、适应未来 工作及进一步发展必需的重要数学知识、基本的数学思想方法和解决数学问题的技能:为 学生进行科学研究和实际工作提供适用的数学方法和计算手段
《线性代数 C》课程教学大纲 一、课程基本信息 课程名称 线性代数 C Linear Algebra C 课程编号 L12021 适用专业 理工、经管类相关专业 课程性质 公共课 总学时 32 学时 学分 2 学分 理论学时 32 学时 实验学时 0 学时 实践学时 0 学时 开课学期 第 2 学期 先修课程 高等数学 后续课程 矩阵分析、数值计算、电路分析、信号处理、测量学、计算机图形学、计算机 辅助设计、密码学等 二、课程性质和课程目标 1.课程性质 线性代数起源于线性方程组的解法,是 19 世纪后期发展起来的一个数学分支,是理 工科专业和经管类专业的一门重要数学基础课,也是硕士研究生入学考试数学科目中的一 部分。通过本课程的学习使学生了解和掌握行列式、矩阵、线性方程组等基本理论和基本 知识,并具有熟练的矩阵运算能力及用矩阵方法解决一些实际问题的能力,提高学生的抽 象思维能力、逻辑推理能力、实际应用能力以及解题的技能与技巧。 2. 课程目标 课程目标 1:理解行列式及余子式、代数余子式的概念,掌握行列式的展开法则;掌 握行列式的基本性质及常见的几种计算行列式的方法;掌握克莱姆法则。 课程目标 2:理解 n 维向量及向量组线性相关、线性无关的概念;掌握向量的线性关 系与线性方程组的联系;掌握判断向量组线性相关及无关的方法;理解最大线性无关组与 向量组秩的概念;会利用矩阵的初等变换求最大线性无关组及矩阵的秩。 课程目标 3:掌握矩阵的基本运算;掌握逆矩阵的概念及其存在的充分必要条件;理 解矩阵的初等变换规则,并会用初等变换法求矩阵的逆;掌握矩阵分块的概念及分块矩阵 的运算规则。 课程目标4:理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解 的充分必要条件;理解齐次线性方程组的基础解系及通解等概念;理解非齐次线性方程组 的解的结构及通解等概念;掌握用初等行变换求线性方程组通解的方法。 课程目标 5:通过线性代数课程的学习,使学生具有较强的线性运算能力、抽象思维 能力、逻辑推理能力、空间想象能力和自学能力等;培养和提高学生运用数学方法分析问 题和解决问题(包括解决实际问题)的意识和能力;使学生获得各专业所需的、适应未来 工作及进一步发展必需的重要数学知识、基本的数学思想方法和解决数学问题的技能;为 学生进行科学研究和实际工作提供适用的数学方法和计算手段
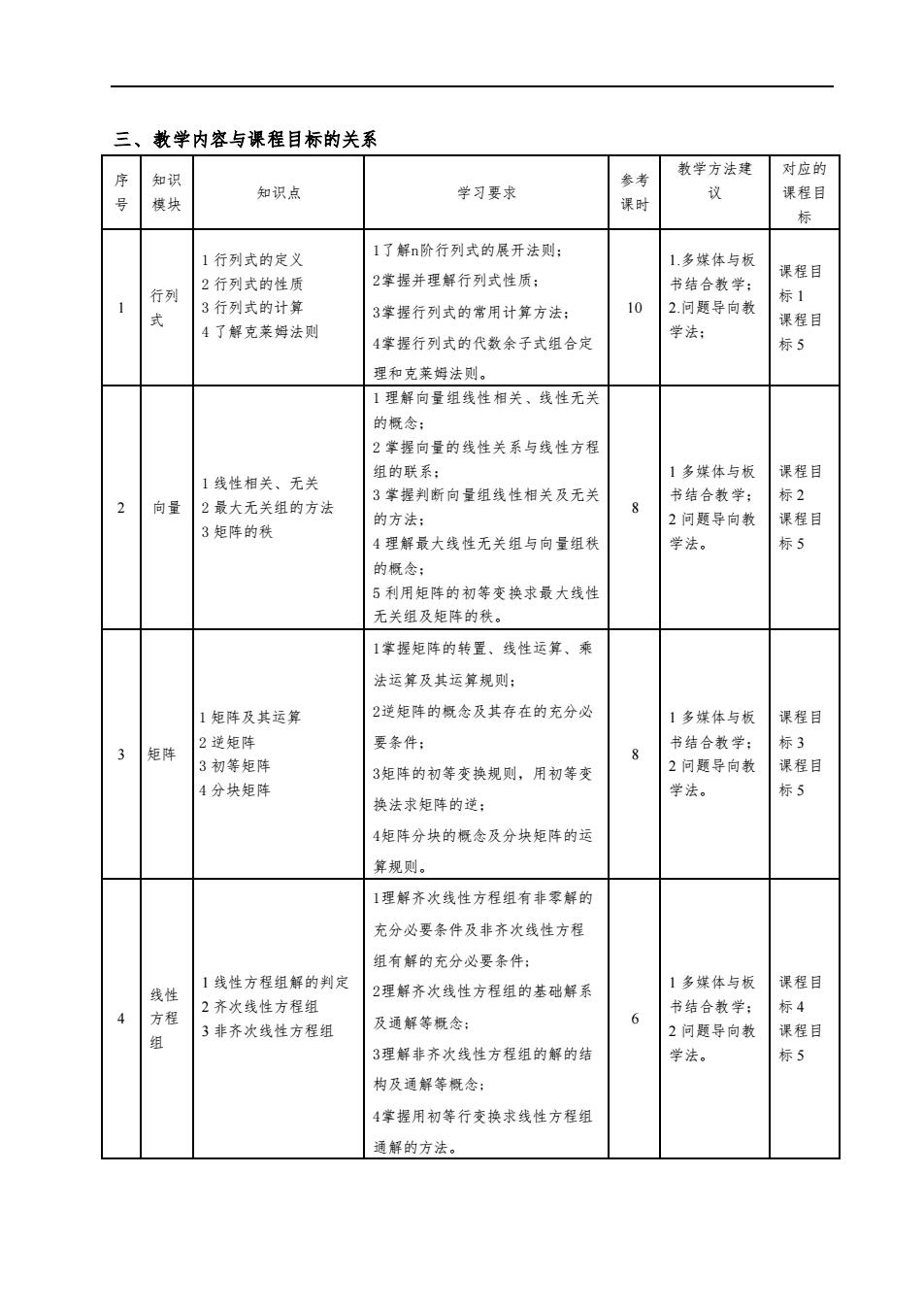
三、 教学内容与课程目标的关系 知识 参考 教学方法建 对应的 知识点 学习要求 课程目 标 行利武的定 1了解n阶行列式的展开法则 1.多媒体与板 2掌提并理解行列式性质: 课程 行列 2行列式的性质 书结合教举 3行列式的计算 3掌握行列式的常用计算方法: 10 2.问题导向教 课程目 4了解克莱姆法则 学法: 4掌握行列式的代数余子式组合定 标5 理和克莱姆法则。 1理解向量组线性相关、线性无关 的概念: 2堂据向量的线性关系与线性方程 组的联系 线性相关、无关 1多媒体与板 2 向量 3掌握判断向量组线性相关及无关 2最大无关组的方法 书结合教学 8 的方法: 2问题导向物 课程目 3矩阵的秩 4理解最大线性无关组与向量组秩 学法。 标5 的概念: 5利用矩阵的初等变换求最大线性 无关组及矩阵的秩 1掌发矩阵的转置、线性运算、乘 法运算及其坛馆翅则 1矩阵及其运算 2逆矩阵的概念及共存在的充分必 1多蝶体与板 课程目 2逆矩阵 要条件: 标3 矩阵 8 书结合教学: 3初等矩阵 3矩牌的初等变换规则,用初等变 2问题导向新 课程目 4分块矩阵 学法。 标5 换法求矩阵的逆: 4矩阵分块的概念及分块矩阵的运 算却则。 1理解齐次线性方程组有非零解的 充分必要条件及非齐次线性方程 组有解的充分必要条件 线 线性方程组解的判定 2理解齐次线性方程组的基础解系 1多媒体与板 课程目 4 2齐次线性方程组 书结合数学: 6 3非齐次线性方程组 及通解等概念: 2问题导向新 课程目 3理解非齐次线性方程组的解的结 学法。 标5 构及通解等概念: 4掌提用初等行变换求线性方程组 通解的方法
三、教学内容与课程目标的关系 序 号 知识 模块 知识点 学习要求 参考 课时 教学方法建 议 对应的 课程目 标 1 行列 式 1 行列式的定义 2 行列式的性质 3 行列式的计算 4 了解克莱姆法则 1了解n阶行列式的展开法则; 2掌握并理解行列式性质; 3掌握行列式的常用计算方法; 4掌握行列式的代数余子式组合定 理和克莱姆法则。 10 1.多媒体与板 书结合教学; 2.问题导向教 学法; 课程目 标 1 课程目 标 5 2 向量 1 线性相关、无关 2 最大无关组的方法 3 矩阵的秩 1 理解向量组线性相关、线性无关 的概念; 2 掌握向量的线性关系与线性方程 组的联系; 3 掌握判断向量组线性相关及无关 的方法; 4 理解最大线性无关组与向量组秩 的概念; 5 利用矩阵的初等变换求最大线性 无关组及矩阵的秩。 8 1 多媒体与板 书结合教学; 2 问题导向教 学法。 课程目 标 2 课程目 标 5 3 矩阵 1 矩阵及其运算 2 逆矩阵 3 初等矩阵 4 分块矩阵 1掌握矩阵的转置、线性运算、乘 法运算及其运算规则; 2逆矩阵的概念及其存在的充分必 要条件; 3矩阵的初等变换规则,用初等变 换法求矩阵的逆; 4矩阵分块的概念及分块矩阵的运 算规则。 8 1 多媒体与板 书结合教学; 2 问题导向教 学法。 课程目 标 3 课程目 标 5 4 线性 方程 组 1 线性方程组解的判定 2 齐次线性方程组 3 非齐次线性方程组 1理解齐次线性方程组有非零解的 充分必要条件及非齐次线性方程 组有解的充分必要条件; 2理解齐次线性方程组的基础解系 及通解等概念; 3理解非齐次线性方程组的解的结 构及通解等概念; 4掌握用初等行变换求线性方程组 通解的方法。 6 1 多媒体与板 书结合教学; 2 问题导向教 学法。 课程目 标 4 课程目 标 5

四、教学方法和学习建议 1.教学方法建议 以教师讲授为主,结合学生的大量练习为主要途径,使学生掌握线性代数的基本理论 和方法。在教学设计中应充分体现以学生为中心的理念,突出学生的主体地位和教师的引 导作用,促进师生之问的交流、互动,全面培养学生的解决问题和分析问题的能力,提高 学生的综合素质。 在教学过程中根据课程内容和学生的实际情况可选择运用的教学方法有以下几类: ()多煤体教学法:板书和多煤体教学相结合,提高课堂教学信息量,增强教学的直 观性 (②)案例教学法:通过分析和研究已有的案例组织教学,使学生能够通过对案例的研 究与发现进行学习,在必要的时候回忆并应用相关知识与技能。在此过程中培养和鼓励学 生的独立思考能力和交流互动能力。 (3)问题驱动教学法:通过提出现实中的实际问题,建立数学模型,使学生在分析问 题和解决问题的过程中提炼知识,提高理论联系实际能力,了解理论知识的实际应用。用 问题鬼动教学,激发学生的学习热情、加蛋讨论交流、增加自主学习,促进学以致用和创 新活动。 除此之外可以根据实际情况灵活运用雨课堂、翻转课堂、小组讨论等教学手段开展教 学活动。鼓励学生充分运用网络教学资源进行自主学习。 每次课后都应布置相应数量的练习题帮助学生巩固所学知识。 习题课是数学类课程实现教学要求的一个重要环节,任课老师可以根据实际教学进 度,几次课程内容之后安排一次习题课,或实行碎片化的习题处理方式即每次上课都处理 几个相关题目。习题课可以帮助老师及时了解学生的知识掌握情况,不可忽略 2.学生学习建议 ()重点学习矩阵的运算及线性方程组的解法,尤其是矩阵的初等变换、特征值及特 征向量、对角化等 (2)课前预习环节。充分发挥自主学习的能动性。通过复习上节课知识,完成相关作 业练习,预习课程内容、登录相关教学平台,资料下载等进行自主学习。 (3)课堂听课环节。专心听课,尽快进入学习状态,听老师讲解,特别是一些定理的 证明过程和题目的演算过程;做好笔记,记录重点,圈出疑难点,以利于课后复习;认真 完成随堂练习,善于思考,大胆质疑,积极回答问题参与课堂互动。 (4)课后复习环节。及时复习巩固,一定要在思想上树立意识,数学类课程一定要多
四、教学方法和学习建议 1.教学方法建议 以教师讲授为主,结合学生的大量练习为主要途径,使学生掌握线性代数的基本理论 和方法。在教学设计中应充分体现以学生为中心的理念,突出学生的主体地位和教师的引 导作用,促进师生之间的交流、互动,全面培养学生的解决问题和分析问题的能力,提高 学生的综合素质。 在教学过程中根据课程内容和学生的实际情况可选择运用的教学方法有以下几类: (1)多媒体教学法:板书和多媒体教学相结合,提高课堂教学信息量,增强教学的直 观性 (2)案例教学法:通过分析和研究已有的案例组织教学,使学生能够通过对案例的研 究与发现进行学习,在必要的时候回忆并应用相关知识与技能。在此过程中培养和鼓励学 生的独立思考能力和交流互动能力。 (3)问题驱动教学法:通过提出现实中的实际问题,建立数学模型,使学生在分析问 题和解决问题的过程中提炼知识,提高理论联系实际能力,了解理论知识的实际应用。用 问题驱动教学,激发学生的学习热情、加强讨论交流、增加自主学习,促进学以致用和创 新活动。 除此之外可以根据实际情况灵活运用雨课堂、翻转课堂、小组讨论等教学手段开展教 学活动。鼓励学生充分运用网络教学资源进行自主学习。 每次课后都应布置相应数量的练习题帮助学生巩固所学知识。 习题课是数学类课程实现教学要求的一个重要环节,任课老师可以根据实际教学进 度,几次课程内容之后安排一次习题课,或实行碎片化的习题处理方式即每次上课都处理 几个相关题目。习题课可以帮助老师及时了解学生的知识掌握情况,不可忽略。 2.学生学习建议 (1)重点学习矩阵的运算及线性方程组的解法,尤其是矩阵的初等变换、特征值及特 征向量、对角化等 (2)课前预习环节。充分发挥自主学习的能动性。通过复习上节课知识,完成相关作 业练习,预习课程内容、登录相关教学平台,资料下载等进行自主学习。 (3)课堂听课环节。专心听课,尽快进入学习状态,听老师讲解,特别是一些定理的 证明过程和题目的演算过程;做好笔记,记录重点,圈出疑难点,以利于课后复习;认真 完成随堂练习,善于思考,大胆质疑,积极回答问题参与课堂互动。 (4)课后复习环节。及时复习巩固,一定要在思想上树立意识,数学类课程一定要多
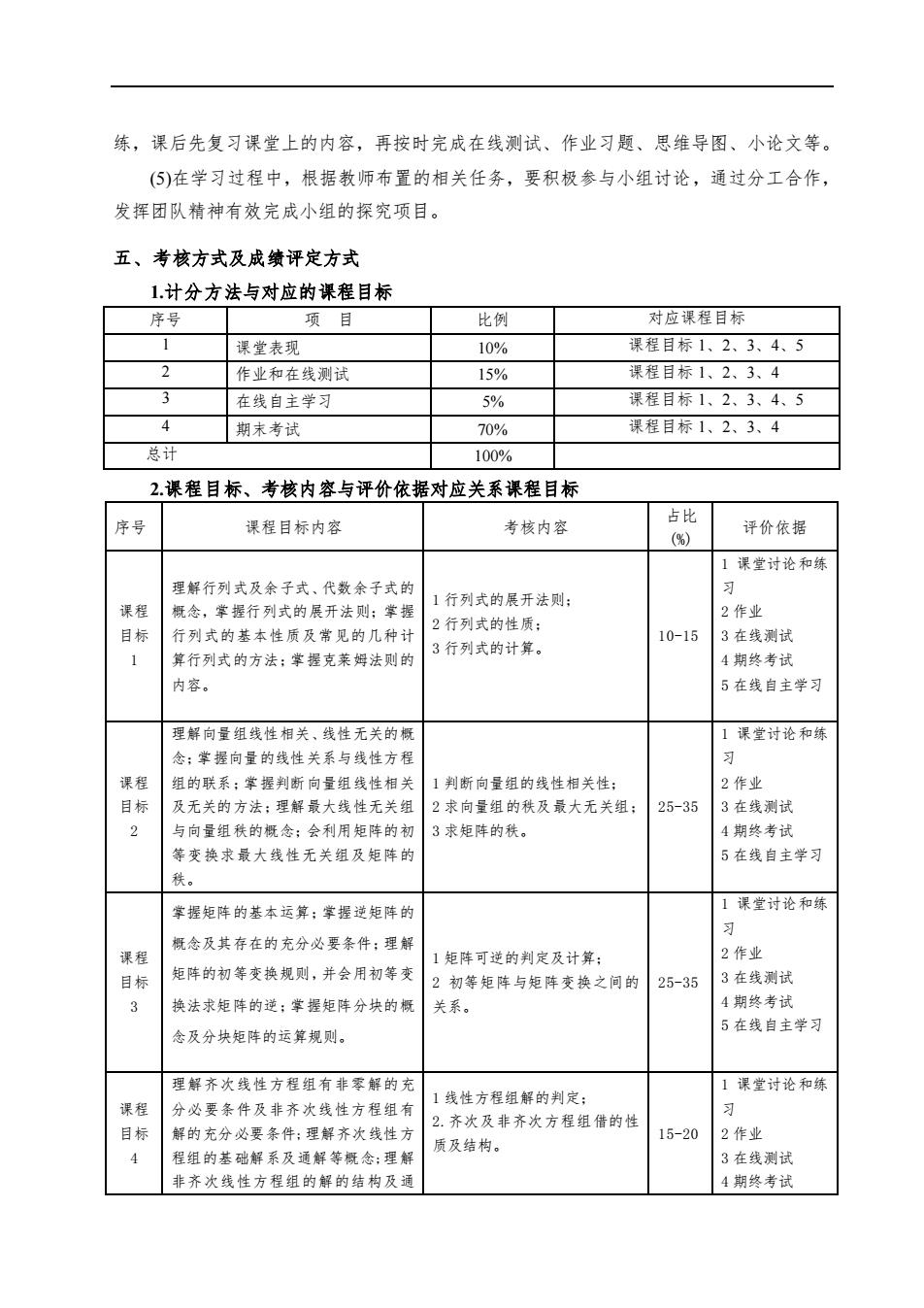
练,课后先复习课堂上的内容,再按时完成在线测试、作业习题、思维导图、小论文等。 (⑤)在学习过程中,根据教师布置的相关任务,要积极参与小组讨论,通过分工合作, 发挥团队精神有效完成小组的探究项目。 五、考核方式及成绩评定方式 1.计分方法与对应的课程目标 序号 项日 比例 对应课程目标 1 课堂表现 10% 课程目标1、2、3、4、5 2 作业和在线测试 15% 课程目标1、2、3、4 3 在线自主学习 5% 课程目标1、2、3、4、5 期末考试 70% 课程目标1、2.3、4 总计 100% 2.渠程目标、考核内容与评价依据对应关系课程目标 序号 课程目标内容 考核内容 评价依据 1课堂讨论和练 理解行列式及余子式、代数余子式的 1行列式的展开法则: 习 课程 概余,堂据行列式的层开法则:堂据 2作业 2行列式的性质: 目标 行列式的基本性质及常见的几种 10-15 3在线测试 算行列式的方法:掌握克莱姆法则的 3行列式的计算 1期终考试 内容, 5在线自主学习 理解向量组线性相关线性无关的橱 1课堂讨论和练 念:掌提向量的线性关系与线性方相 组的联系:掌握判断向量组线性相 判断向量组的线性相关性 2作业 及无关的方法:理解最大线性无关 2求向量组的秩及最大无关组 25-35 3在线测试 2 与向量组秩的概念:会利用矩阵的莉 3求矩阵的扶, 4期终考试 等变换求最大线性无关组及矩阵的 5在线自主学习 秩。 掌据矩阵的基本运算:掌握逆矩阵的 1课堂讨论和练 习 概念及其存在的充分必要条件:理 课程 矩阵可述的判定及计算 2作业 目标 矩阵的初等变换规则,并会用初等变 初等矩阵与矩阵变换之问的 25-35 3在缘测试 换法求矩阵的逆:掌握矩阵分块的橱 关系。 4期终考试 3 5在线自主学 念及分块矩阵的运算规则。 理解齐次线性方程组有非零解的充 1课堂讨论和练 线性方程组解的判定: 课程 分必要条件及非齐次线性方程组有 目标 2.齐次及非齐次方程组借的性 解的充分必要条件:理解齐次线性方 15-20 2作业 得细的解系及通解:理解 质及结构。 3在线测 非齐次线性方程组的解的结构及通 4期终考试
练,课后先复习课堂上的内容,再按时完成在线测试、作业习题、思维导图、小论文等。 (5)在学习过程中,根据教师布置的相关任务,要积极参与小组讨论,通过分工合作, 发挥团队精神有效完成小组的探究项目。 五、考核方式及成绩评定方式 1.计分方法与对应的课程目标 序号 项 目 比例 对应课程目标 1 课堂表现 10% 课程目标 1、2、3、4、5 2 作业和在线测试 15% 课程目标 1、2、3、4 3 在线自主学习 5% 课程目标 1、2、3、4、5 4 期末考试 70% 课程目标 1、2、3、4 总计 100% 2.课程目标、考核内容与评价依据对应关系课程目标 序号 课程目标内容 考核内容 占比 (%) 评价依据 课程 目标 1 理解行列式及余子式、代数余子式的 概念,掌握行列式的展开法则;掌握 行列式的基本性质及常见的几种计 算行列式的方法;掌握克莱姆法则的 内容。 1 行列式的展开法则; 2 行列式的性质; 3 行列式的计算。 10-15 1 课堂讨论和练 习 2 作业 3 在线测试 4 期终考试 5 在线自主学习 课程 目标 2 理解向量组线性相关、线性无关的概 念;掌握向量的线性关系与线性方程 组的联系;掌握判断向量组线性相关 及无关的方法;理解最大线性无关组 与向量组秩的概念;会利用矩阵的初 等变换求最大线性无关组及矩阵的 秩。 1 判断向量组的线性相关性; 2 求向量组的秩及最大无关组; 3 求矩阵的秩。 25-35 1 课堂讨论和练 习 2 作业 3 在线测试 4 期终考试 5 在线自主学习 课程 目标 3 掌握矩阵的基本运算;掌握逆矩阵的 概念及其存在的充分必要条件;理解 矩阵的初等变换规则,并会用初等变 换法求矩阵的逆;掌握矩阵分块的概 念及分块矩阵的运算规则。 1 矩阵可逆的判定及计算; 2 初等矩阵与矩阵变换之间的 关系。 25-35 1 课堂讨论和练 习 2 作业 3 在线测试 4 期终考试 5 在线自主学习 课程 目标 4 理解齐次线性方程组有非零解的充 分必要条件及非齐次线性方程组有 解的充分必要条件;理解齐次线性方 程组的基础解系及通解等概念;理解 非齐次线性方程组的解的结构及通 1 线性方程组解的判定; 2.齐次及非齐次方程组借的性 质及结构。 15-20 1 课堂讨论和练 习 2 作业 3 在线测试 4 期终考试
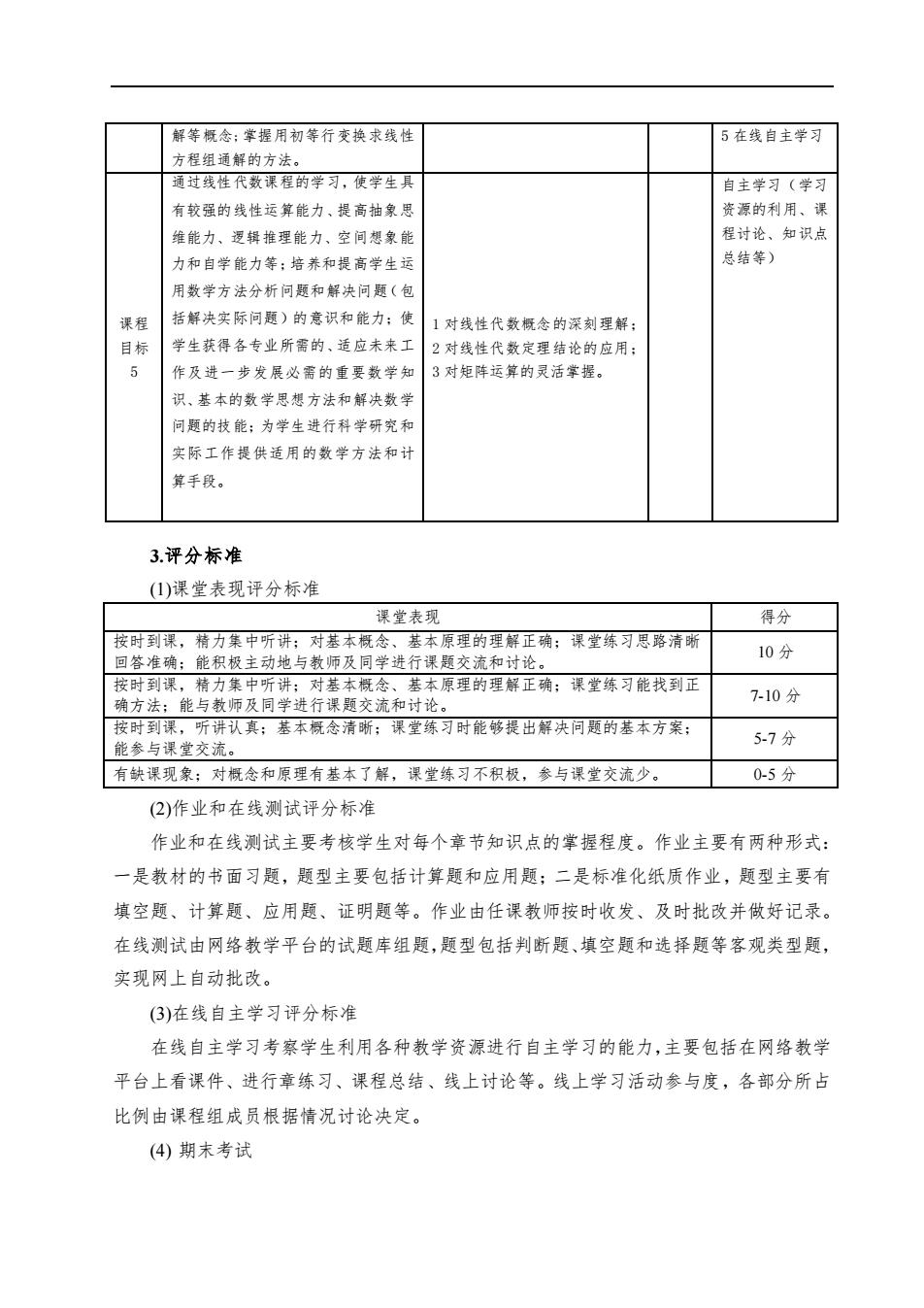
解等概念:掌握用初等行变换求线性 5在线自主学习 方架组通鲤的方达 通过线性代数课程的学习,使学生具 自主学习(学习 有较强的线性运算能力、提高抽象思 资源的利用、课 维能力,罗辑推理能力、空间想象能 程讨论、知识点 力和自学能力等:培养和提高学生西 总结等) 用赘学方法分析间顺和解决间颗(句 课程 括解决实际问题)的意识和能力:使 1对线性代数橱余的深刻理解 目标 学生获得各专业所需的、适应未来工?对等格代数定理结论的应用 作及进一步发展必需的重要数学知 3对矩阵运算的灵活掌握。 识、基本的数学思想方法和解决数学 问数的技能:为学生进行科学研究和 实际工作提供适用的数学方法和 算手段。 3.评分标准 (1)课堂表现评分标准 误堂表现 得分 按时到课,精力集 理解正确;课堂练习思路清晰 10分 行课题交流和 原理的理解正确课堂练习能找到正 7-10分 能袋与误堂交流。 真:基本概念清:课堂练习时能够提出解决问题的基本方案 5-7分 有缺课现象:对概念和原理有基本了解,课堂练习不积极,参与课堂交流少。 0-5分■ (2)作业和在线测试评分标准 作业和在线测试主要考核学生对每个章节知识点的掌握程度。作业主要有两种形式: 一是教材的书面习题,题型主要包括计算题和应用题:二是标准化纸质作业,题型主要有 填空题、计算题、应用题、证明题等。作业由任课教师按时收发、及时批改并做好记录。 在线测试由网络教学平台的试题库组题,题型包括判断题、填空题和选择题等客观类型题, 实现网上自动批改。 (3)在线自主学习评分标准 在线自主学习考察学生利用各种教学资源进行自主学习的能力,主要包括在网络教学 平台上看课件、进行章练习、课程总结、线上讨论等。线上学习活动参与度,各部分所占 比例由课程组成员根据情况讨论决定。 (4)期末考试
解等概念;掌握用初等行变换求线性 方程组通解的方法。 5 在线自主学习 课程 目标 5 通过线性代数课程的学习,使学生具 有较强的线性运算能力、提高抽象思 维能力、逻辑推理能力、空间想象能 力和自学能力等;培养和提高学生运 用数学方法分析问题和解决问题(包 括解决实际问题)的意识和能力;使 学生获得各专业所需的、适应未来工 作及进一步发展必需的重要数学知 识、基本的数学思想方法和解决数学 问题的技能;为学生进行科学研究和 实际工作提供适用的数学方法和计 算手段。 1 对线性代数概念的深刻理解; 2 对线性代数定理结论的应用; 3 对矩阵运算的灵活掌握。 自主学习(学习 资源的利用、课 程讨论、知识点 总结等) 3.评分标准 (1)课堂表现评分标准 课堂表现 得分 按时到课,精力集中听讲;对基本概念、基本原理的理解正确;课堂练习思路清晰 回答准确;能积极主动地与教师及同学进行课题交流和讨论。 10 分 按时到课,精力集中听讲;对基本概念、基本原理的理解正确;课堂练习能找到正 确方法;能与教师及同学进行课题交流和讨论。 7-10 分 按时到课,听讲认真;基本概念清晰;课堂练习时能够提出解决问题的基本方案; 能参与课堂交流。 5-7 分 有缺课现象;对概念和原理有基本了解,课堂练习不积极,参与课堂交流少。 0-5 分 (2)作业和在线测试评分标准 作业和在线测试主要考核学生对每个章节知识点的掌握程度。作业主要有两种形式: 一是教材的书面习题,题型主要包括计算题和应用题;二是标准化纸质作业,题型主要有 填空题、计算题、应用题、证明题等。作业由任课教师按时收发、及时批改并做好记录。 在线测试由网络教学平台的试题库组题,题型包括判断题、填空题和选择题等客观类型题, 实现网上自动批改。 (3)在线自主学习评分标准 在线自主学习考察学生利用各种教学资源进行自主学习的能力,主要包括在网络教学 平台上看课件、进行章练习、课程总结、线上讨论等。线上学习活动参与度,各部分所占 比例由课程组成员根据情况讨论决定。 (4) 期末考试