
§1.复数 说,用复数及复变函数作工具是十分有效的,这正是由于复数可以 表示平面向量的缘故. 3.复数的模与辐角表示复数之的位置,也可以借助于 点z的极坐标r和0来确定(图1.1).这里使原点与直角坐标系的 原点重合,极轴与正实轴重合 下面我们用向量Oz来表示复数之=x十iy,其中x,y顺次等于 沿x轴与y轴的分量.向量O的长度称为复数:的模或绝对 值,以符号引z或r表示,因而有 r=|z|=x+y2≥0, 且=0的充要条件是之=0. 这里引进的模的概念与对于实数的绝对值的概念是一致的, 由于复数z的模z是非负实数,所以能够比较大小.同样,复数的 实、虚部也能够比较大小 根据图1.1,我们有不等式 |x≤|zl,yl≤|xl,x≤|x+ly, -|x|≤Re≤|x,-z≤lmx≤|x|. (1.1) 根据图1.2,我们有不等式 +|≤1|+|x2 (1.2) (三角形两边之和大于第三边), 它称为三角不等式 此外,根据图1.3,我们还有不等式 1川21|-|21川≤z1-21 (1.3) (三角形两边之差小于第三边) (1.2)及(1.3)中等号成立的几何意义是:复数1,2所表示的两 个向量共线且同向.即 1≠0,22≠0时,21=22(k>0). 用数学归纳法可得推广了的三角不等式

第一章复数与复变函数 |a1十2+.+xn≤x1|+|x2|+.+|x.(1.2) 由图1.3可见,1一2表示点与点2的距离,记为 d(x1,2)=1一x2. 两复数差的模的这个几何意义是非常重要的.它还可以借助解析 几何中两点间的距离公式用解析方法得出: |1-2|=|(x1十iy1)-(x2+iy2)| =√(x1-x2)+(0y-). 实轴正向到非零复数之=x十iy所对应的向量O间的夹角0合于 称为复数x的辐角(Argument),记为 0=Arg z. 我们知道,任一非零复数x有无穷多个辐角,今以arg之表示 其中的一个特定值,并称适合条件 一π<argz≤π (1.4) 的一个为Argx的主值,或称之为x的主辐角.于是 0=Arg之=argz十2kπ (1.5) (k=0,士1,士2,.). 注意当=0时,辐角无意义. 当arg2(:≠0)表:的主辐角时,它与反正切Arctan兰的主 值arctan兰有如下关系(图1.5,图l.6)(注意-元<arg≤π, -<arctan兰<):
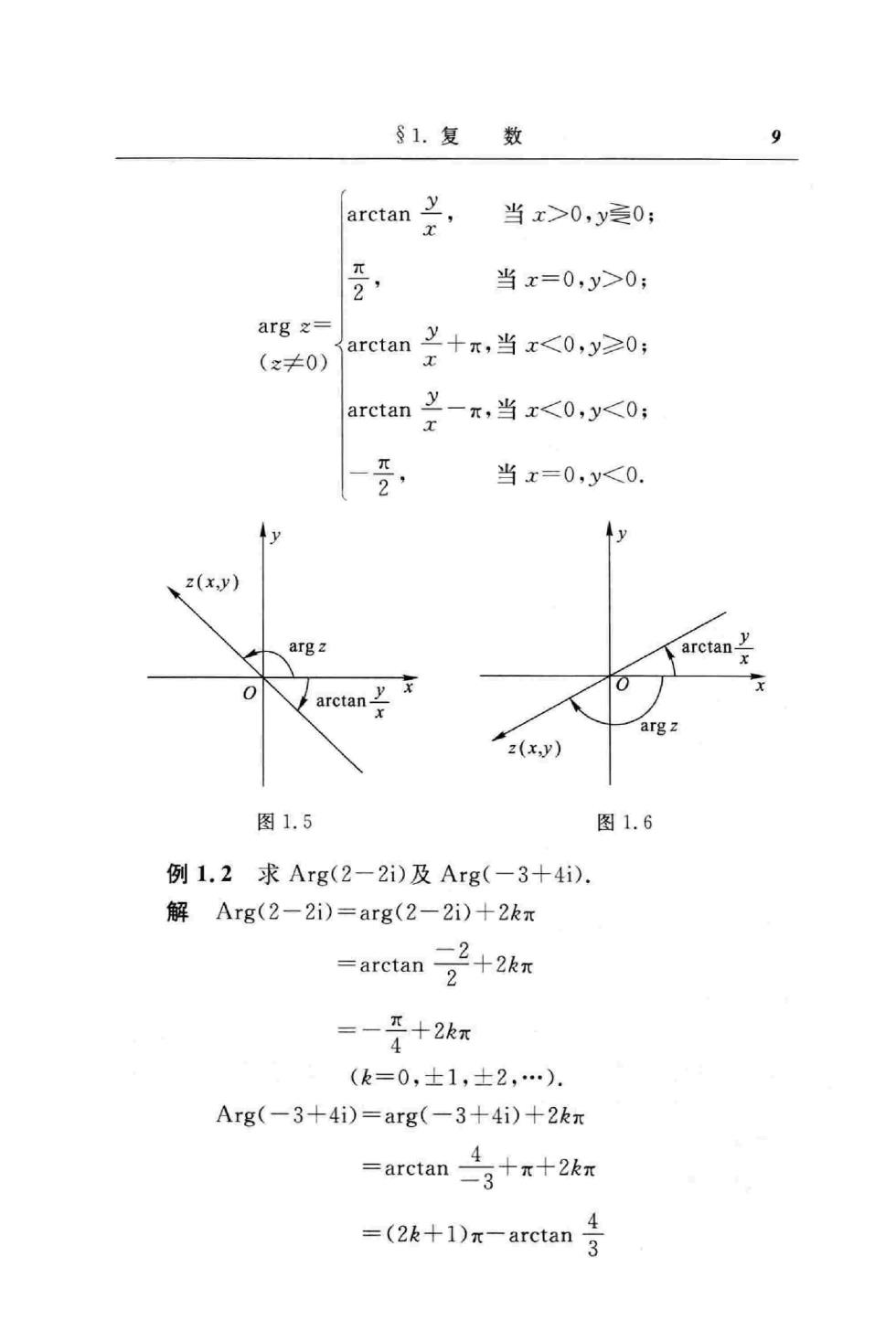
§1.复数 当x>0,y爱0; 当x=0,y>0; arg之= arctan¥+x,当x<0,y>0; (x≠0) , 当x=0,y<0. y 、z(xy) arg arctan- argz z(xy) 图1.5 图1.6 例1.2求Arg(2-2i)及Arg(-3+4i) 解Arg(2-2i)=arg(2-2i)+2kπ =-+2kx (k=0,士1,士2,.) Arg(-3+4i)=arg(-3+4i)+2kπ 4 =arctan3十x+2kr =(2+1Dx-arctan号

10 第一章复数与复变函数 (k=0,±1,±2,.). 例1.3已知流体在某点M的速度v=一1一i,求其大小和 方向. 解大小:=√2; 方向:argw=arctan}x=-8平 从直角坐标与极坐标的关系,我们可以用复数的模r与辐角日 来表示非零复数,即(由图1.1) z=r(cos 0+i sin 0). (1.6) 特别,当r=1时有 z=cos 0++i sin 0, 这种复数称为单位复数 我们引出熟知的欧拉公式: ei=cos 0i sin 0, (1.7) 并且容易验证 e9e4=ec4+4),】 2=ew (1.8) 利用公式(1.7),就可以把(1.6)改写成 之=re9. (1.9) 也就是说,任一非零复数:总可以表成 eiar : (1.9) 这里的arg之不必取主值. 我们分别称(1.6)式及(1.9)(或(1.9))式为非零复数x的三 角形式和指数形式,并称x=x十iy为复数x的代数形式.复数的 这三种表示法可以互相转换,以适应讨论不同问题时的需要,且使 用起来各有其便 例1.4 1+i=/2(cos +isin=2et;

§1.复数 11 i=1·(cos交+isin)=e; 1=1.(cos 0+i sin 0)=ei; -2=2(cosπ十isinπ)=2e; -3i=3cos(←受)+isim(-)]=3e. 还有e=-i,e=-1,e2m=1(k为整数). 例1.5将复数 1-cosp+i sin(0<p≤π) 化为指数形式。 解原式=2sin号+2isin号cos号 =2sin号[sin号+icos号】 =2sin号cos(登-号)+isin(径-号)] =2sin号c(传-)1 当之=x十iy≠0,记arg之=0(主值),则 tam号=平8o80,fes0x+V2+亏 sin 0 rsin 6 y 所以argz=0(主值)=2 arctan x+√x+y 对于名1=r1e,2=r2e8,则 x1=x2台r1=r2,0,=02(或01=02十2kπ,k为整数). 利用复数的指数形式作乘除法较简单.因由(1.8)可立得 名=ne9re=nrne+),】 (1.10)