
如以转角为输出,系统的运动方程为 (2)激磁电流控制方式 (1-6) 假设电枢电流i。=Ct(常数),再设气隙磁通与 激磁电流成正比 电压平衡方程和转矩平衡方程为 u;=RLe (1-8) )-阳oT (1-9) 式中T,是负载转矩 电机的电磁转矩 Ti=Kin (1-7)
如以转角为输出,系统的运动方程为 ⑵ 激磁电流控制方式 假设电枢电流 (常数),再设气隙磁通与 激磁电流 成正比 电压平衡方程和转矩平衡方程为 电机的电磁转矩 (1-6) (1-8) (1-9) (1-7) 式中 是负载转矩 a a a e t a Ktua dt d K K R b dt d R J bL dt d L J ( ) ( ) 2 2 3 3 i Ct a f i dt di u R i L f f f f f f b TL dt d T J f f f T K i TL

·电机的微分方程为 ,+(1-,安R0=K, (1-10) +J-,+R=K, (1-11) 研究参量不同,它们的数学描述也不同 以上几个方程有一个共同点: 它们都是只描述了输入(4aur)与输出(0、0) 之间的关系一系统的输入输出描述 (3)如果不消去变量i。,可以得到系统的另一种数学 描述
电机的微分方程为 研究参量不同,它们的数学描述也不同 以上几个方程有一个共同点: 它们都是只描述了输入( )与输出( ) 之间的关系——系统的输入输出描述 ⑶ 如果不消去变量 ,可以得到系统的另一种数学 描述 (1-10) (1-11) f f f f f f R b K u dt d R J bL dt d L J ( ) 2 2 f f f f K f u f dt d R b dt d R J bL dt d L J 2 2 3 3 ( ) a f u 、u 、 a i

将转矩公式(1一1)和反电势公式(1一2)分别代入 转矩平衡方程(1一4)和电压平衡方程(1一3)得 do K.:bT dt -ia- 0+ (1-12) J J di。 L L a (1-13) 设T=0, 令输入a=u,输出0=”y及ia=出 1 0=x2, 并将它们写成矩阵形式 Ra Ke La La 6- (1-14) y=[ 1] X2
将转矩公式(1-1)和反电势公式(1-2)分别代入 转矩平衡方程(1-4)和电压平衡方程(1-3)得 设 ,令输入 ,输出 及 , ,并将它们写成矩阵形式 (1-12) (1-13) (1-14) 2 x J T J b i J K dt d L a t a a e a a a a a di R K u i dt L L L TL 0 ua u y 1 i x a 2 1 2 1 2 1 [ 0 1 ] 0 1 x x y L u x x J b J K L K L R x x a t a e a a

同样,将激磁控制的方程经过整理,设T,=0,并令 输入ur=u,输出0=y,及i,=x1,0=x2可得 + u b LX2 (1-15) 1 y=[ 0 1] X2 前面两组向量方程,不仅描述了系统外部变量(输入与 输出),而且描述了系统内部变量(i。或if)的行为。这 就是系统的状态空间描述。 使用数学的方法不同,系统的数学模型也不同
同样,将激磁控制的方程经过整理,设 ,并令 输入 ,输出 ,及 可得 前面两组向量方程,不仅描述了系统外部变量(输入与 输出),而且描述了系统内部变量( 或 )的行为。这 就是系统的状态空间描述。 使用数学的方法不同,系统的数学模型也不同 (1-15) TL 0 u u f y 1 2 i x , x f L u x x J b J K L R x x f f f f 0 0 1 2 1 2 1 2 1 [ 0 1 ] x x y a i f i
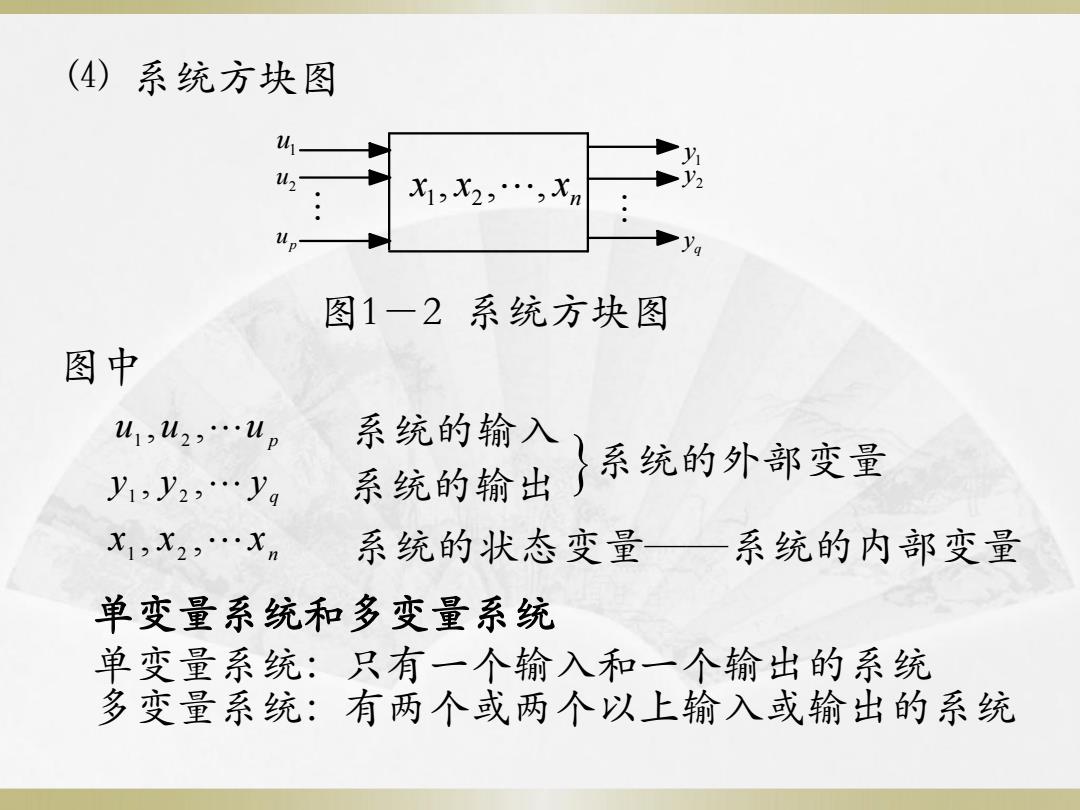
(4)系统方块图 y 2 X1,X2…,Xn 图1一2系统方块图 图中 u1,u2,…lp 系统的输入 y1,y2,…yg 系统的输出 }系统的外部变量 X1,X2,…Xn 系统的状态变量一 系统的内部变量 单变量系统和多变量系统 单变量系统:只有一个输入和一个输出的系统 多变量系统:有两个或两个以上输入或输出的系统
⑷ 系统方块图 图中 系统的输入 系统的输出 系统的状态变量——系统的内部变量 系统的外部变量 图1-2 系统方块图 单变量系统和多变量系统 单变量系统:只有一个输入和一个输出的系统 多变量系统:有两个或两个以上输入或输出的系统 u1 up 2 u 1 y 2 y q y n x , x , , x 1 2 p u ,u ,u 1 2 q y , y , y 1 2 n x , x ,x 1 2