
基本回路与基本回路系统 定理16.4设T为无向连通图G的一棵生成树,e为T 的任意一条弦,则TUe中含一条弦其余边均为树 枝的圈,而且不同的弦对应的圈也不同, 证:设=(w,y),由定理知,在T中,w,y之间存在惟 一的路径ITu,y,则TyUe满足要求,不同的弦对 应的圈显然是一同的
定理16.4 设T为无向连通图G的一棵生成树,e为T 的任意一条弦,则T∪ e中含一条弦其余边均为树 枝的圈, 而且不同的弦对应的圈也不同. 证:设e=(u,v),由定理知, 在T中, u,v 之间存在惟 一的路径(u,v),则(u,v)∪ e满足要求,不同的弦对 应的圈显然是一同的。 基本回路与基本回路系统

基本回路与基本回路系统 定义设T是n阶m条边的无向连通图G的一棵生成 树,设e1,e2,e'mnt1为T的弦.设C,为T添加弦e, 产生的G中惟一的圈(由e,'和树枝组成),称C为对应 弦e,'的基本回路或基本圈,=1,2,m-n+1.称{C1) C2,Cm+}为对应T的基本回路系统, 称m-n+1为G的圈秩,记为(G). 求基本回路的算法:设弦=(u,y),先求T中u到v的路径 ITu,再并上弦e,即得对应e的基本回路
基本回路与基本回路系统 定义 设T是n阶m条边的无向连通图G的一棵生成 树,设e1 , e2 , . , e mn+1为T的弦. 设Cr为T添加弦er 产生的G中惟一的圈(由er 和树枝组成), 称Cr为对应 弦er 的基本回路或基本圈, r=1, 2, ., mn+1. 称{C1 , C2 , ., Cmn+1 }为对应T的基本回路系统. 称mn+1为G的圈秩,记为ξ(G) . 求基本回路的算法: 设弦e=(u,v), 先求T中u到v的路径 (u,v) , 再并上弦e, 即得对应e的基本回路
实例 例图中红边为一棵生成树, 求对应它的基本回路系统 解弦e,g对应的基本回路分别为 C-e bc,Cf-fabc,Cg-gabcd, C基={Ce Cp Ca
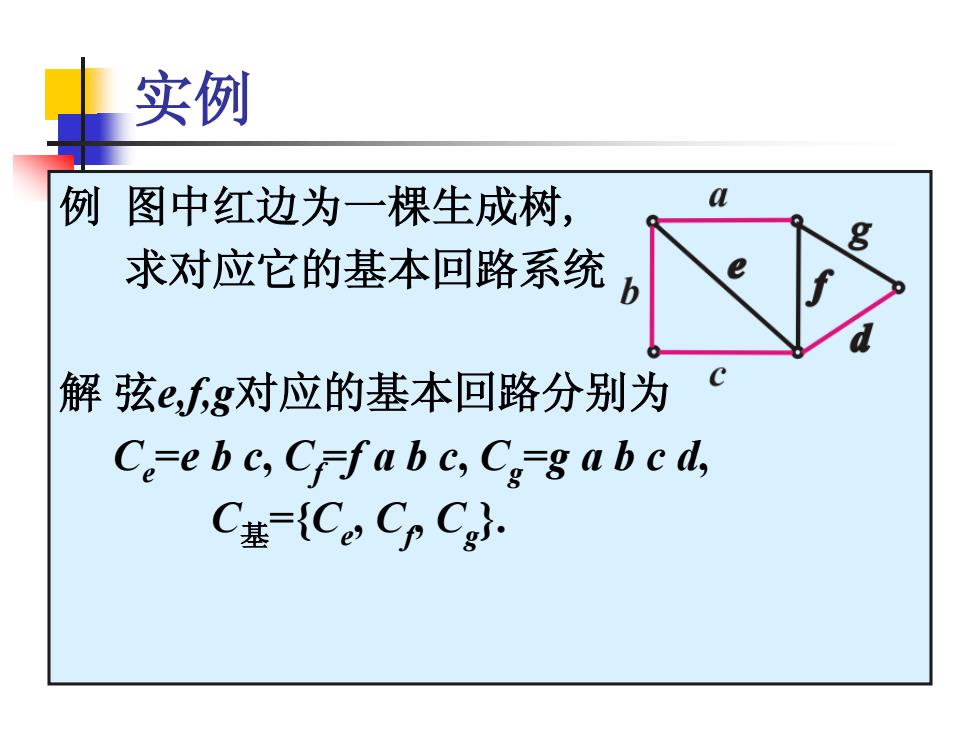
实例 例 图中红边为一棵生成树, 求对应它的基本回路系统 解 弦e,f,g对应的基本回路分别为 Ce =e b c, Cf =f a b c, Cg =g a b c d, C基={Ce , Cf , Cg }