
第十三章格与布尔代数
第十三章 格与布尔代数

§13.1格的定义与性质 定义设<S,≤>是偏序集,如果Vx,yES, x,y}都有最小上界和最大下界,则称S关于 ≤构成一个格
定义 设<S, ≼>是偏序集,如果 x,y∈S, {x,y}都有最小上界和最大下界, 则称S关于 ≼构成一个格. §13.1 格的定义与性质
【例】设S12=了1,2,3,4,6,12是12的因子构成的集合。其 的整除关系R=<xJ>lxES12个JyES12∧x整除y7,R是S12H 的偏序关系,<S12,R是偏序集。写出S12上的覆盖关系 COVS2,画出哈斯图,验证偏序集<S12,R是格。 解:S12上的覆盖关系 C0VS12=<1,2>,<1,3>,<2,4>,<2,6>, <3,6>,<4,12>,<6,12>7, 哈斯图如图8.1所示。从哈斯图中可看出, 集合S2的任意两个元素都有最小上界 和最大下界,故偏序集<S12,R心是格。 图8.1
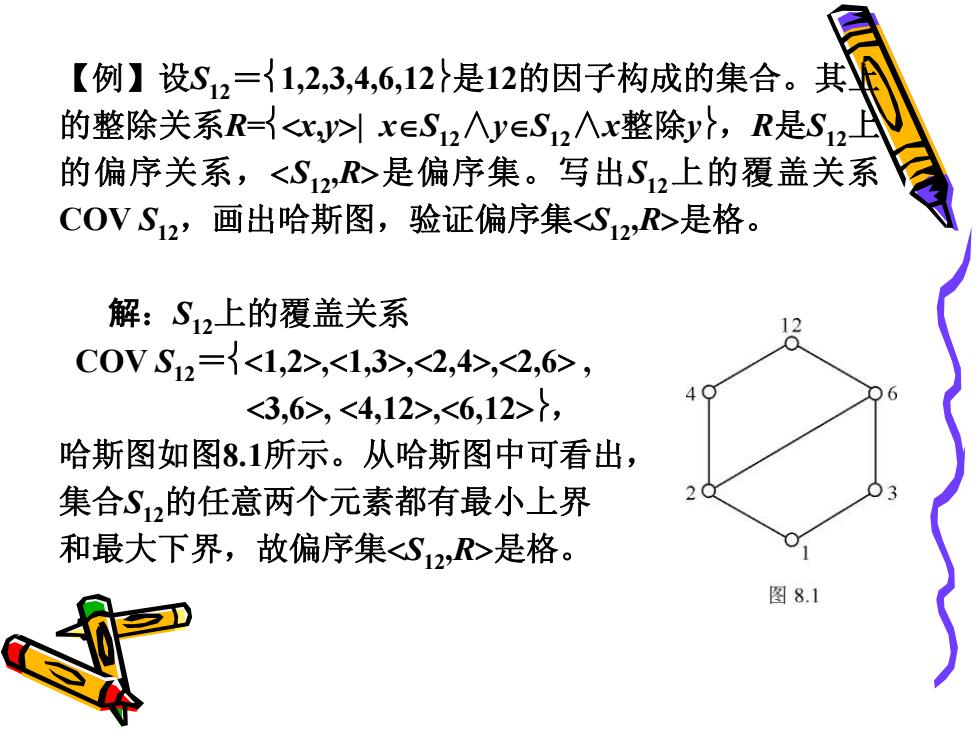
【例】设S12 =1,2,3,4,6,12是12的因子构成的集合。其上 的整除关系R=x,y| xS12∧yS12∧x整除y,R是S12上 的偏序关系,S12,R是偏序集。写出S12上的覆盖关系 COV S12,画出哈斯图,验证偏序集S12,R是格。 解:S12上的覆盖关系 COV S12 =1,2,1,3,2,4,2,6 , 3,6, 4,12,6,12, 哈斯图如图8.1所示。从哈斯图中可看出, 集合S12的任意两个元素都有最小上界 和最大下界,故偏序集S12,R是格

xVy表示x和y的最小上界 x∧y表示x和y的最大下界 V和∧在本章中只是格中的运算符,不表 示逻辑上的合取与析取
x∨y表示x和y的最小上界 x∧y表示x和y的最大下界. ∨和∧在本章中只是格中的运算符,不表 示逻辑上的合取与析取

例1设n为正整数,Sn为n的正因子的集合, D为整除关系,则<S,D>构成格. Vx,yE Sn, xVy是x,y的最小公倍数[x,y],1cm(x,y) x∧y是x,y的最大公约数(x,y),gcd(x,y)
例1 设n为正整数,Sn为n的正因子的集合, D为整除关系,则<Sn,D>构成格. x,y∈Sn, x∨y是x,y的最小公倍数[x,y],lcm(x,y) x∧y是x,y的最大公约数(x,y),gcd(x,y)