
例题 例1已知无向树T中,有1个3度顶点,2个2度顶点,其余顶点全 是树叶.试求树叶数,并画出满足要求的非同构的无向树. 解用树的性质n-1和握手定理。 设有x片树叶,于是n=1+2+x=3+x, 2m=2(n-1)=2×(2+x)=1×3+2x2+x 解出x=3,故T有3片树叶. T的度数列为1,1,1,2,2,3 有2棵非同构的无向树,如图所示
例题 例1 已知无向树T中, 有1个3度顶点, 2个2度顶点, 其余顶点全 是树叶. 试求树叶数, 并画出满足要求的非同构的无向树. 解 用树的性质m=n1和握手定理. 设有x片树叶,于是 n=1+2+x=3+x, 2m=2(n1)=2(2+x)=13+22+x 解出x=3,故T有3片树叶. T的度数列为1, 1, 1, 2, 2, 3 有2棵非同构的无向树, 如图所示
例题 例2已知无向树T有5片树叶,2度与3度顶点各1个,其余顶点 的度数均为4.求T的阶数,并画出满足要求的所有非同构 的无向树 解设T的阶数为n,则边数为n-1,4度顶点的个数为n-7.由握 手定理得 2t=2(n-1)=5×1+2×1+3x1+4(n-7) 解出n=8,4度顶点为1个, T的度数列为1,1,1,1,1,2,3,4 有3棵非同构的无向树 中
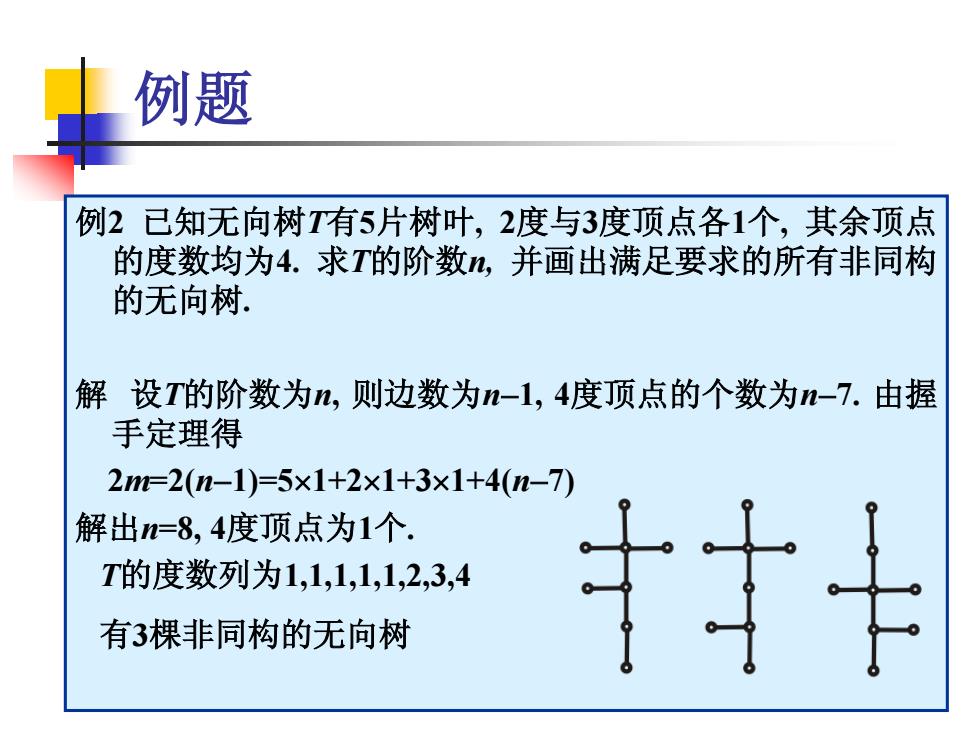
例题 例2 已知无向树T有5片树叶, 2度与3度顶点各1个, 其余顶点 的度数均为4. 求T的阶数n, 并画出满足要求的所有非同构 的无向树. 解 设T的阶数为n, 则边数为n1, 4度顶点的个数为n7. 由握 手定理得 2m=2(n1)=51+21+31+4(n7) 解出n=8, 4度顶点为1个. T的度数列为1,1,1,1,1,2,3,4 有3棵非同构的无向树

16.2 生成树 ■生成树、树枝、弦、余树 ■基本回路与基本回路系统 ■基本割集与基本割集系统 ■最小生成树
16.2 生成树 生成树、树枝、弦、余树 基本回路与基本回路系统 基本割集与基本割集系统 最小生成树
生成树 设G为无向连通图 G的生成树:G的生成子图并且是树 生成树T的树枝:G在T中的边 生成树T的弦:G不在T中的边 生成树T的余树T:所有弦的集合的导出子图 注意:T不一定连通,也不一定不含回路。 右图黑边构成生成树 红边构成余树
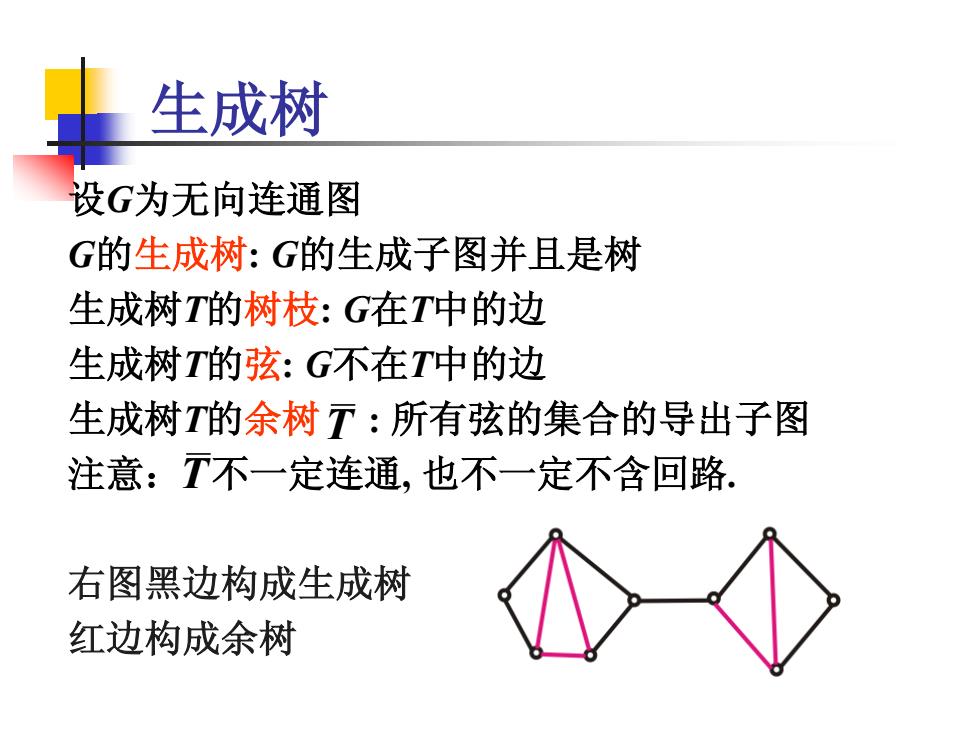
生成树 T T 设G为无向连通图 G的生成树: G的生成子图并且是树 生成树T的树枝: G在T中的边 生成树T的弦: G不在T中的边 生成树T的余树 : 所有弦的集合的导出子图 注意: 不一定连通, 也不一定不含回路. 右图黑边构成生成树 红边构成余树

生成树的存在性 定理任何无向连通图都有生成树. 证用破圈法.若图中无圈,则图本身就是自己的生成树 否则删去圈上的任一条边,这不破坏连通性,重复进行 直到无圈为止,剩下的图是一棵生成树. 推论1设n阶无向连通图有m条边,则m2n-1, 推论2设阶无向连通图有m条边,则它的生成树的余树 有m-n+1条边. 推论3设T为G的生成树T的余树,C为G中任意一 个圈,则C与下一定有公共边
生成树的存在性 定理 任何无向连通图都有生成树. 证 用破圈法. 若图中无圈, 则图本身就是自己的生成树. 否则删去圈上的任一条边, 这不破坏连通性, 重复进行 直到无圈为止,剩下的图是一棵生成树. 推论1 设n阶无向连通图有m条边, 则mn1. 推论2 设n阶无向连通图有m条边, 则它的生成树的余树 有mn+1条边. 推论3 设 为G的生成树 T 的余树,C 为G 中任意一 个圈,则C与 一定有公共边. T T