福州大学：《离散数学》课程教学资源（课件讲稿）第十七章 平面图及图的着色

第十七章平面图 ■平面图的基本概念 ■欧拉公式 ■平面图的判断 ■平面图的对偶图 ■图中顶点的着色 ■地图的着色与平面图的着色 边着色

第十七章 平面图  平面图的基本概念  欧拉公式  平面图的判断  平面图的对偶图  图中顶点的着色  地图的着色与平面图的着色  边着色

17.1平面图的基本概念 ■平面图与平面嵌入 ■平面图的面、有限面、无限面 ■面的次数 ·极大平面图 ■极小非平面图

17.1 平面图的基本概念  平面图与平面嵌入  平面图的面、有限面、无限面  面的次数  极大平面图  极小非平面图

平面图和平面嵌入 定义如果能将图G除顶点外边不相交地画在平面上， 则称G是平面图.这个画出的无边相交的图称作G 的平面嵌入.没有平面嵌入的图称作非平面图. 例如下图中(1)(4)是平面图，(2)是(1)的平面嵌入， (4)是3)的平面嵌入.（⑤）是非平面图. (1) (2) (3) (4) (5)

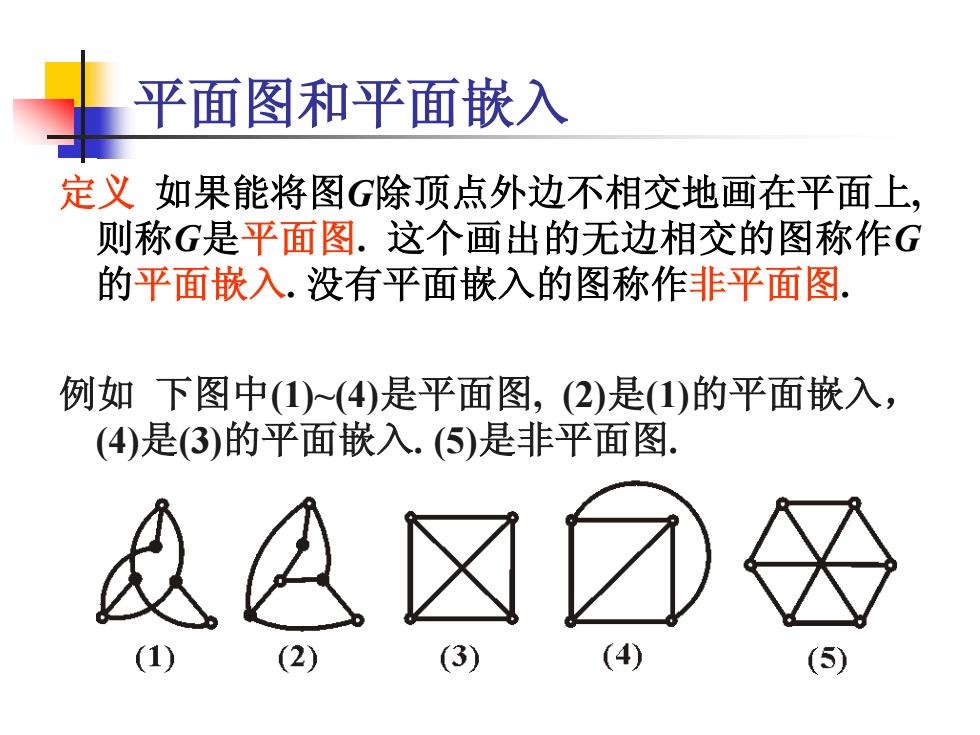
平面图和平面嵌入 定义 如果能将图G除顶点外边不相交地画在平面上, 则称G是平面图. 这个画出的无边相交的图称作G 的平面嵌入. 没有平面嵌入的图称作非平面图. 例如 下图中(1)~(4)是平面图, (2)是(1)的平面嵌入， (4)是(3)的平面嵌入. (5)是非平面图

平面图和平面嵌入（续) ●1 按定义，平面图不一定是平面嵌入.但今后讨论平面图时， 可根据上下文加以区分. 。K和K.3是非平面图 。Ke和K2.3是平面图 K 设GcG,若G为平面图，则G也是 平面图；若G为非平面图，则G也 是非平面图. 。Kn(25),K3n(n23)都是非平面图. 飞33 平行边与环不影响图的平面性

平面图和平面嵌入(续) • 按定义, 平面图不一定是平面嵌入. 但今后讨论平面图时, 可根据上下文加以区分. • K5和K3,3是非平面图 • K5 -e和K2,3是平面图 • 设GG, 若G为平面图, 则G也是 平面图; 若G为非平面图, 则G也 是非平面图. • Kn (n5), K3,n (n3)都是非平面图. • 平行边与环不影响图的平面性. K5 K3,3

平面图的面与次数 设G是一个平面嵌入 G的面：由G的边将平面划分成的每一个区域 无限面（外部面）：面积无限的面，用R表示 有限面（内部面）：面积有限的面，用R1,R2,R表示 面R的边界：包围R的所有边构成的回路组 面R的次数：边界的长度，用deg(R)表示 说明：构成一个面的边界的回路组可能是初级回路，简单回 路，也可能是复杂回路，甚至还可能是非连通的回路之并， 定理平面图各面的次数之和等于边数的2倍

平面图的面与次数 设G是一个平面嵌入 G的面: 由G的边将平面划分成的每一个区域 无限面(外部面): 面积无限的面, 用R0表示 有限面(内部面): 面积有限的面, 用R1 , R2 ,., Rk表示 面Ri的边界: 包围Ri的所有边构成的回路组 面Ri的次数: Ri边界的长度，用deg(Ri )表示 说明: 构成一个面的边界的回路组可能是初级回路, 简单回 路, 也可能是复杂回路, 甚至还可能是非连通的回路之并. 定理 平面图各面的次数之和等于边数的2倍